科学空间|Scientific Spaces

用理论物理来卷机器学习已经不是什么新鲜事了，比如上个月介绍的《生成扩散模型漫谈（十三）：从万有引力到扩散模型》就是经典一例。最近一篇新出的论文《Self-Supervised Learning based on Heat Equation》，顾名思义，用热传导方程来做（图像领域的）自监督学习，引起了笔者的兴趣。这种物理方程如何在机器学习中发挥作用？同样的思路能否迁移到NLP中？让我们一起来读读论文。

基本方程

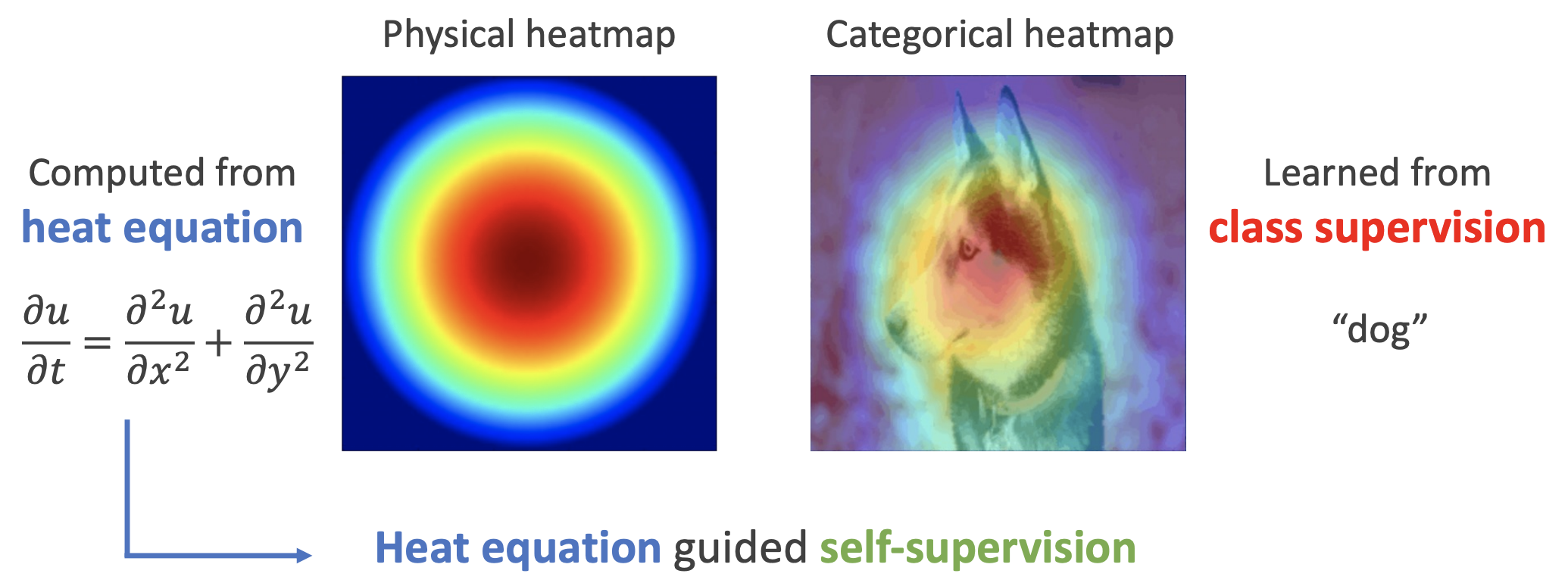
如下图，左边是物理中热传导方程的解，右端则是CAM、积分梯度等显著性方法得到的归因热力图，可以看到两者有一定的相似之处，于是作者认为热传导方程可以作为好的视觉特征的一个重要先验。

热方程的热力图（左）和视觉模型的热力图（右）

点击阅读全文...

在文章《生成扩散模型漫谈（六）：一般框架之ODE篇》中，我们推导了SDE的Fokker-Planck方程；而在《生成扩散模型漫谈（十二）：“硬刚”扩散ODE》中，我们单独推导了ODE的连续性方程。它们都是描述随机变量沿着SDE/ODE演化的分布变化方程，连续性方程是Fokker-Planck方程的特例。在推导Fokker-Planck方程时，我们将泰勒展开硬套到了狄拉克函数上，虽然结果是对的，但未免有点不伦不类；在推导连续性方程时，我们结合了雅可比行列式和泰勒展开，方法本身比较常规，但没法用来推广到Fokker-Planck方程。

这篇文章我们介绍“测试函数法”，它是推导连续性方程和Fokker-Planck方程的标准方法之一，其分析过程比较正规，并且适用场景也比较广。

点击阅读全文...

这篇文章我们继续来闭门造车，分享一下笔者最近对多模态学习的一些新理解。

在前文《“闭门造车”之多模态思路浅谈（一）：无损输入》中，我们强调了无损输入对于理想的多模型模态的重要性。如果这个观点成立，那么当前基于VQ-VAE、VQ-GAN等将图像离散化的主流思路就存在能力瓶颈，因为只需要简单计算一下信息熵就可以表明离散化必然会有严重的信息损失，所以更有前景或者说更长远的方案应该是输入连续型特征，比如直接将图像的原始像素特征Patchify后输入到模型中。

然而，连续型输入对于图像理解自然简单，但对图像生成来说则引入了额外的困难，因为非离散化无法直接套用文本的自回归框架，多少都要加入一些新内容如扩散，这就引出了本文的主题——如何进行多模态的自回归学习与生成。当然，非离散化只是表面的困难，更艰巨的部份还在后头...

无损含义

首先我们再来明确一下无损的含义。无损并不是指整个计算过程中一丁点损失都不能有，这不现实，也不符合我们所理解的深度学习的要义——在2015年的文章《闲聊：神经网络与深度学习》我们就提到过，深度学习成功的关键是信息损失。所以，这里无损的含义很简单，单纯是希望作为模型的输入来说尽可能无损。

点击阅读全文...

当要求函数的最小值时，我们通常会先求导函数然后寻找其零点，比较幸运的情况下，这些零点之一正好是原函数的最小值点。如果是向量函数，则将导数改为梯度并求其零点。当梯度零点不易求得时，我们可以使用梯度下降来逐渐逼近最小值点。

以上这些都是无约束优化的基础结果，相信不少读者都有所了解。然而，本文的主题是概率空间中的优化，即目标函数的输入是一个概率分布，这类目标的优化更为复杂，因为它的搜索空间不再是无约束的，如果我们依旧去求解梯度零点或者执行梯度下降，所得结果未必能保证是一个概率分布。因此，我们需要寻找一种新的分析和计算方法，以确保优化结果能够符合概率分布的特性。

对此，笔者一直以来也感到颇为头疼，所以近来决定”痛定思痛“，针对概率分布的优化问题系统学习了一番，最后将学习所得整理在此，供大家参考。

点击阅读全文...

随着算力的飞速进步，有越多越多的场景希望能够实现“算力换时间”，即通过堆砌算力来缩短模型训练时间。理想情况下，我们希望投入$n$倍的算力，那么达到同样效果的时间则缩短为$1/n$，此时总的算力成本是一致的。这个“希望”看上去很合理和自然，但实际上并不平凡，即便我们不考虑通信之类的瓶颈，当算力超过一定规模或者模型小于一定规模时，增加算力往往只能增大Batch Size。然而，增大Batch Size一定可以缩短训练时间并保持效果不变吗？

这就是接下来我们要讨论的话题：当Batch Size增大时，各种超参数尤其是学习率该如何调整，才能保持原本的训练效果并最大化训练效率？我们也可以称之为Batch Size与学习率之间的Scaling Law。

方差视角

直觉上，当Batch Size增大时，每个Batch的梯度将会更准，所以步子就可以迈大一点，也就是增大学习率，以求更快达到终点，缩短训练时间，这一点大体上都能想到。问题就是，增大多少才是最合适的呢？

点击阅读全文...

这几天在重温去年的Meta的一篇论文《A Theory on Adam Instability in Large-Scale Machine Learning》，里边给出了看待Adam等自适应学习率优化器的新视角：它指出梯度平方的滑动平均某种程度上近似于在估计Hessian矩阵的平方，从而Adam、RMSprop等优化器实际上近似于二阶的Newton法。

这个角度颇为新颖，而且表面上跟以往的一些Hessian近似有明显的差异，因此值得我们去学习和思考一番。

牛顿下降

设损失函数为$\mathcal{L}(\boldsymbol{\theta})$，其中待优化参数为$\boldsymbol{\theta}$，我们的优化目标是
\begin{equation}\boldsymbol{\theta}^* = \mathop{\text{argmin}}_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\label{eq:loss}\end{equation}
假设$\boldsymbol{\theta}$的当前值是$\boldsymbol{\theta}_t$，Newton法通过将损失函数展开到二阶来寻求$\boldsymbol{\theta}_{t+1}$：
\begin{equation}\mathcal{L}(\boldsymbol{\theta})\approx \mathcal{L}(\boldsymbol{\theta}_t) + \boldsymbol{g}_t^{\top}(\boldsymbol{\theta} - \boldsymbol{\theta}_t) + \frac{1}{2}(\boldsymbol{\theta} - \boldsymbol{\theta}_t)^{\top}\boldsymbol{\mathcal{H}}_t(\boldsymbol{\theta} - \boldsymbol{\theta}_t)\end{equation}

点击阅读全文...

在查找量子化有关资料的时候，笔者查找到了一系列名为《漫谈几何量子化》的文章，并进一步查询得知，作者为季候风，原来发表在繁星客栈（顺便提一下，繁星客栈是最早的理论物理论坛之一，现在已经不能发帖了，但是上面很多资料都弥足珍贵），据说这是除正则量子化和路径积分量子化外的第三种量子化方法。网上鲜有几何量子化的资料，更不用说是中文资料了，于是季候风前辈的这一十五篇文章便显得格外有意义了。

然而，虽然不少网站都转载了这系列文章，但是无一例外地，文章中的公式图片已经失效了，后来笔者在百度网盘那找到其中的十四篇pdf格式的（估计是网友在公式图片失效前保存下来的），笔者通过替换公式服务器的方式找回了第十五篇，把第十五篇也补充进去了。（见漫谈几何量子化（原文档）.zip）

虽然这样已经面前能够阅读了，但是总感觉美中不足，虽然笔者花了三天时间把文章重新用$\LaTeX$录入了，主要是把公式重新录入了，简单地排版了一下。现放出来与大家分享。

点击阅读全文...

生成模型一直是笔者比较关注的主题，不管是NLP和CV的生成模型都是如此。这篇文章里，我们介绍一个新颖的生成模型，来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》，论文中称之为EAE（Entropic AutoEncoder）。它要做的事情给变分自编码器（VAE）基本一致，最终效果其实也差不多（略优），说它新颖并不是它生成效果有多好，而是思路上的新奇，颇有别致感。此外，借着这个机会，我们还将学习一种统计量的估计方法——$k$邻近方法，这是一种很有用的非参数估计方法。

自编码器vs生成模型

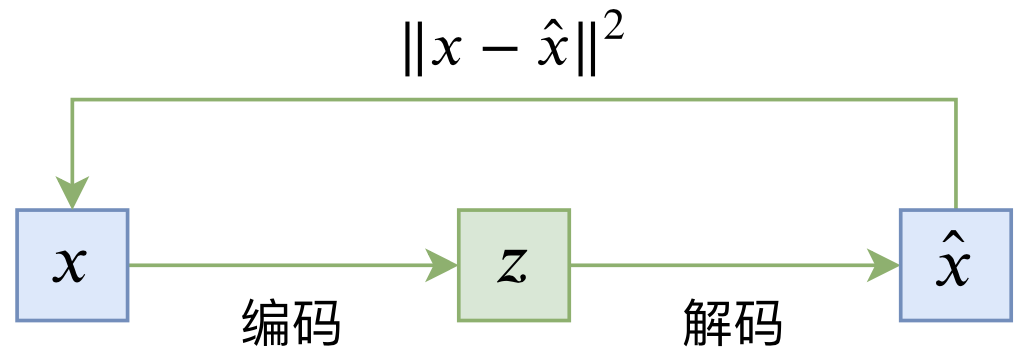
普通的自编码器是一个“编码-解码”的重构过程，如下图所示：

典型自编码器示意图

其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}

点击阅读全文...