2
May
基于Conv1D的光谱分类模型（一维序列分类）
By 苏剑林 | 2018-05-02 | 116895位读者 | 引用前段时间天池出了个天文数据挖掘竞赛——LAMOST光谱分类（将对应的光谱识别为4类中的一类），虽然没有奖金，但还是觉得挺有意思，所以就报名参加了。做了一段时间，成绩自我感觉还可以，然而最后我却忘记了（或者说根本就没留意到）初赛最后两天还有一步是提交新的测试集结果，然后就没有然后了，留下了一个未竟的模型，可谓“出师未捷身先死”，还是被自己弄死的～
天文数据挖掘大赛——天体光谱智能分类
后来跟其他参赛选手讨论了一下，发现其实我的这个模型还是不错的。当时我记得初赛第一名的成绩是0.83+，而我当时的成绩是0.82+，排名大概是第4、5左右，而且据说很多分数在0.8+的队伍都已经使用了融合模型，而我这0.82+的成绩仅仅是单模型的结果～在平时的群聊中发现也有不少朋友在做一维序列分类模型，而光谱分类本质上也就是一个一维的序列分类，所以分享一下模型，估计对相关朋友会有一定的参考价值。
模型
事实上也不是什么特别的模型，就是普通的一维卷积加残差，对于熟悉图像处理的朋友，这实在是再普通不过的结构了。
27
Oct
什么时候多进程的加速比可以大于1？
By 苏剑林 | 2019-10-27 | 58122位读者 | 引用多进程或者多线程等并行加速目前已经不是什么难事了，相信很多读者都体验过。一般来说，我们会有这样的结论：多进程的加速比很难达到1。换句话说，当你用10进程去并行跑一个任务时，一般只能获得不到10倍的加速，而且进程越多，这个加速比往往就越低。
要注意，我们刚才说“很难达到1”，说明我们的潜意识里就觉得加速比最多也就是1。理论上确实是的，难不成用10进程还能获得20倍的加速？这不是天上掉馅饼吗？不过我前几天确实碰到了一个加速比远大于1的例子，所以在这里跟大家分享一下。
词频统计
我的原始任务是统计词频：我有很多文章，然后我们要对这些文章进行分词，最后汇总出一个词频表出来。一般的写法是这样的：
tokens = {}
for text in read_texts():
for token in tokenize(text):
tokens[token] = tokens.get(token, 0) + 1这种写法在我统计THUCNews全部文章的词频时，大概花了20分钟。
20
Jul
两千美元的汽车----世界最便宜汽车在印度上路!
By 苏剑林 | 2009-07-20 | 16347位读者 | 引用
18
Jul
日全食多路联合直播频道
By 苏剑林 | 2009-07-18 | 17042位读者 | 引用
18
May
鱼与熊掌兼得：融合检索和生成的SimBERT模型
By 苏剑林 | 2020-05-18 | 287058位读者 | 引用前段时间我们开放了一个名为SimBERT的模型权重，它是以Google开源的BERT模型为基础，基于微软的UniLM思想设计了融检索与生成于一体的任务，来进一步微调后得到的模型，所以它同时具备相似问生成和相似句检索能力。不过当时除了放出一个权重文件和示例脚本之外，未对模型原理和训练过程做进一步说明。在这篇文章里，我们来补充这部分内容。
UniLM
UniLM是一个融合NLU和NLG能力的Transformer模型，由微软在去年5月份提出来的，今年2月份则升级到了v2版本。我们之前的文章《从语言模型到Seq2Seq：Transformer如戏，全靠Mask》就简单介绍过UniLM，并且已经集成到了bert4keras中。
UniLM的核心是通过特殊的Attention Mask来赋予模型具有Seq2Seq的能力。假如输入是“你想吃啥”，目标句子是“白切鸡”，那UNILM将这两个句子拼成一个：[CLS] 你 想 吃 啥 [SEP] 白 切 鸡 [SEP]，然后接如图的Attention Mask：
UniLM的Mask
4
Jan
智能家居之热水器零冷水技术原理浅析
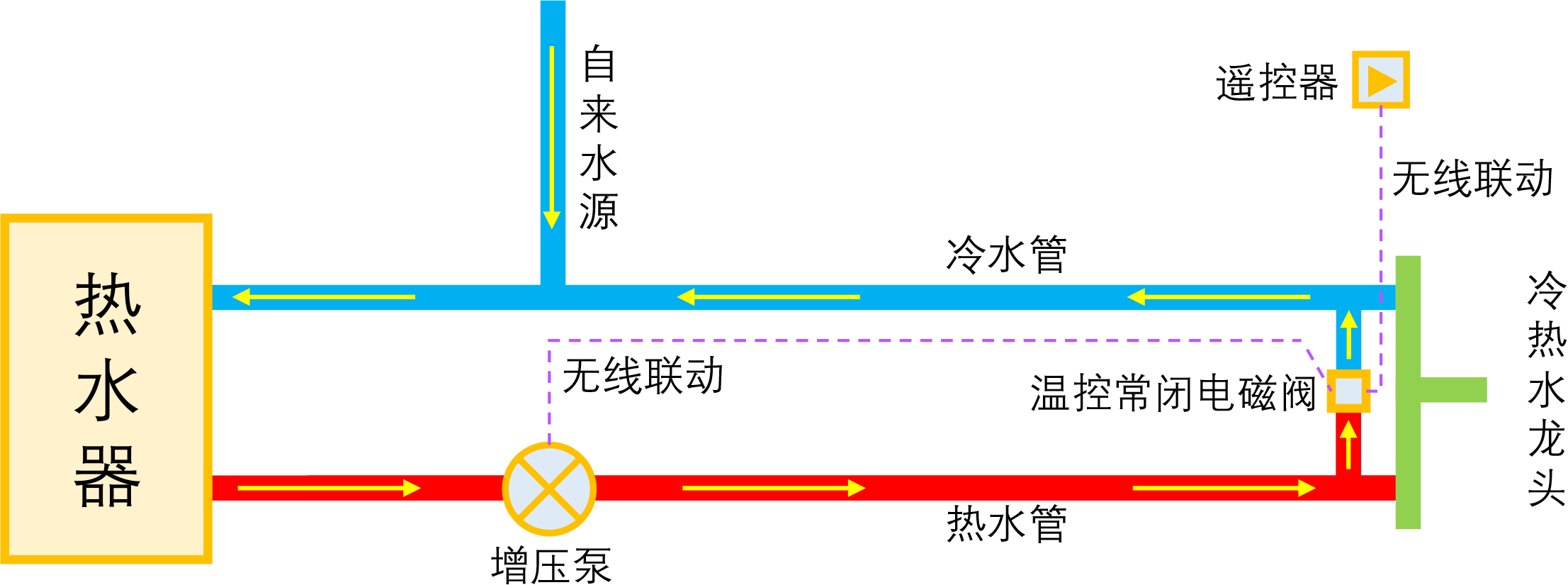
By 苏剑林 | 2023-01-04 | 42479位读者 | 引用如果家庭使用单一的热水器集中供热水，那么当我们想要用热水时，往往需要先放一段时间的冷水，而如果放冷水时间比较长的话，就会比较影响体验。所谓零冷水，实际上就是想办法提前把热水管中的冷水排放掉，以达到（几乎）瞬间出热水的效果。事实上，零冷水并不是什么高大上的技术，但可能由于观念没跟上、理解上有误等原因，零冷水技术还没有在家庭中得到普及，不过随着大家对生活品质的要求越来越高，零冷水确实在慢慢流行起来了。
本文来简单分析一下零冷水技术的实现原理，包括各种方案的优缺点和自省DIY的参考思路。
理想的零冷水方案
写在前面
在文章开始，需要纠正很多人的一个错误观念：零冷水不是为了省钱，而是为了提升生活品质。如果你是省钱最大的心态，那么接下来的内容就可以不用看了，零冷水技术对你毫无价值。
13
Sep
美绘制太空引力高速路帮飞船穿越太阳系(图)
By 苏剑林 | 2009-09-13 | 19105位读者 | 引用
方轮自行车
你见过正方形轮子的自行车吗？一般认为，只有圆形的车轮才能使我们的车子平稳向前移动，但这只是针对平直道路而言的。谁规定路一定是平的？只要铺好一条适当的道路，正方形车轮的自行车照样可以平稳前行！本文就让我们为方轮自行车铺一条路。
其实，方轮自行车已经不是新鲜玩意了，它早已出现在不少科技馆中。从图片中可以看到，它的特殊轨道是有许多段弧组成的，每一段弧的长度等于正方形的边长。车轮前行时，正方形会保持与弧形相切（确保不会打滑）。这样的路的形状是什么曲线呢？很幸运，它并不十分复杂，而且让人意外的是，它就是我们之前已经研究过的“悬链线”！原来，要设计这样的一个曲线的轨道，不需要多么高深的设计师，只需要我们手拿一条铁链，让它自由垂下......
最近评论