科学空间|Scientific Spaces

在最优化问题中，求一个函数的最大值或最小值，最直接的方法是求导，然后比较各阶极值的大小。然而，我们所要优化的函数往往不一定可导，比如函数中含有最大值函数$\max(x,y)$的。这时候就得求助于其他思路了。有一个很巧妙的思路是，将这些不可导函数用一个可导的函数来近似它，从而我们用求极值的方法来求出它近似的最优值。本文的任务，就是探究一个简单而有用的函数，它能够作为最大值函数的近似，并且具有多阶导数。下面是笔者给出的一个推导过程。

在数学分析中，笔者已经学习过一个关于最大值函数的公式，即当$x \geq 0, y \geq 0$时，我们有
$$\max(x,y)=\frac{1}{2}\left(|x+y|+|x-y|\right)\tag{1}$$
那么，为了寻求一个最大值的函数，我们首先可以考虑寻找一个能够近似表示绝对值$|x|$的函数，这样我们就把问题从二维降低到一维了。那么，哪个函数可以使用呢？

点击阅读全文...

神经网络

在所有机器学习模型之中，也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番，说一次神经网络。当然，本文并不打算从头开始介绍神经网络，只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友，请移步阅读下面的教程：
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程

http://blog.csdn.net/zouxy09/article/details/8775360

机器分类

这里以分类工作为例，数据挖掘或机器学习中，有很多分类的问题，比如讲一句话的情况进行分类，粗略点可以分类为“积极”或“消极”，精细点分为开心、生气、忧伤等；另外一个典型的分类问题是手写数字识别，也就是将图片分为10类（0,1,2,3,4,5,6,7,8,9）。因此，也产生了很多分类的模型。

点击阅读全文...

前言：四五月份的时候，我参加了两个数据挖掘相关的竞赛，分别是物电学院举办的“亮剑杯”，以及第三届 “泰迪杯”全国大学生数据挖掘竞赛。很碰巧的是，两个比赛中，都有一题主要涉及到中文情感分类工作。在做“亮剑杯”的时候，由于我还是初涉，水平有限，仅仅是基于传统的思路实现了一个简单的文本情感分类模型。而在后续的“泰迪杯”中，由于学习的深入，我已经基本了解深度学习的思想，并且用深度学习的算法实现了文本情感分类模型。因此，我打算将两个不同的模型都放到博客中，供读者参考。刚入门的读者，可以从中比较两者的不同，并且了解相关思路。高手请一笑置之。

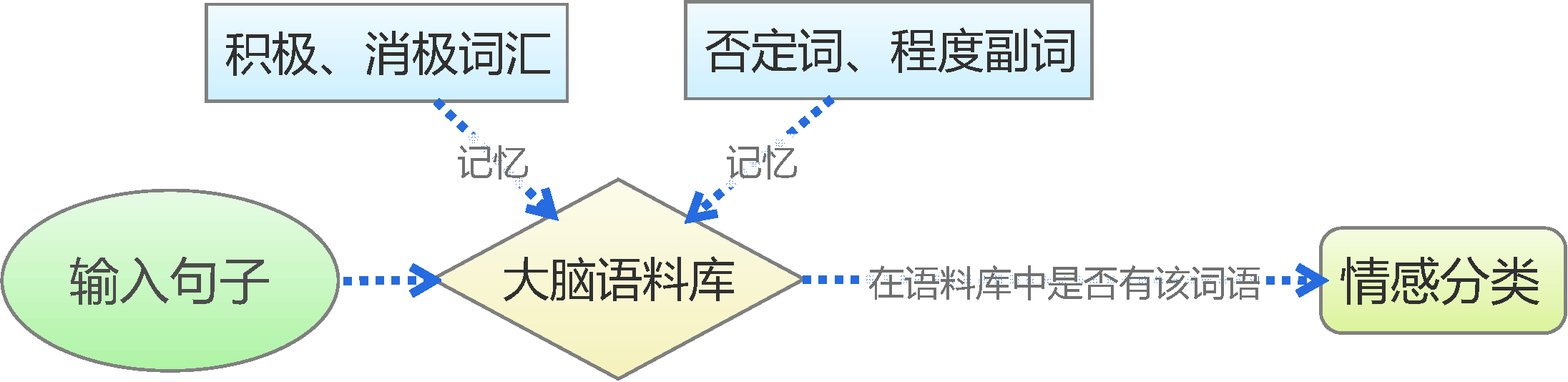
基于情感词典

人的最简单的判断思维

点击阅读全文...

最新更新：《用Numpy实现高效的Apriori算法》

最近在做数据挖掘相关的工作，阅读到了Apriori算法。平时由于没有涉及到相关领域，因此对Apriori算法并不了解，而如今工作上遇到了，就不得不认真学习一下了。Apriori算法是一个寻找关联规则的算法，也就是从一大批数据中找到可能的逻辑，比如“条件A+条件B”很有可能推出“条件C”（A+B-->C），这就是一个关联规则。具体来讲，比如客户买了A商品后，往往会买B商品（反之，买了B商品不一定会买A商品），或者更复杂的，买了A、B两种商品的客户，很有可能会再买C商品（反之也不一定）。有了这些信息，我们就可以把一些商品组合销售，以获得更高的收益。而寻求关联规则的算法，就是关联分析算法。

啤酒与尿布

啤酒与尿布

关联算法的案例中，最为人老生常谈的应该是“啤酒与尿布”了。“啤酒与尿布”的故事产生于20世纪90年代的美国沃尔玛超市中，超市管理人员发现“啤酒与尿布两件看上去毫无关系的商品会经常出现在同一个购物篮中”。经过分析，原来在美国有婴儿的家庭中，一般是母亲在家中照看婴儿，年轻的父亲前去超市购买尿布。父亲在购买尿布的同时，往往会顺便为自己购买啤酒，这样就会出现啤酒与尿布这两件看上去不相干的商品经常会出现在同一个购物篮的现象。因此，沃尔玛尝试将啤酒与尿布摆放在相同的区域，让年轻的父亲可以同时找到这两件商品。事实是效果相当不错！

点击阅读全文...

本文主要做了一个尝试，尝试不通过Green公式而实现将封闭曲线的面积与线积分相互转换。这种转换的思路，因为仅仅利用了二重积分的积分变换，较为容易理解，而且易于推广。至于这种技巧是否真正具有实际价值，还请读者评论。

假设平面上一条简单封闭曲线由以下参数方程给出：
$$\begin{equation}\left\{\begin{aligned}x = f(t)\\y = g(t)\end{aligned}\right.\end{equation}$$
其中参数$t$位于某个区间$[a,b]$上，即$f(a)=f(b),g(a)=g(b)$。现在的问题是，求该封闭曲线围成的区域的面积。

点击阅读全文...

语言处理

在《文本情感分类（一）：传统模型》一文中，笔者简单介绍了进行文本情感分类的传统思路。传统的思路简单易懂，而且稳定性也比较强，然而存在着两个难以克服的局限性：一、精度问题，传统思路差强人意，当然一般的应用已经足够了，但是要进一步提高精度，却缺乏比较好的方法；二、背景知识问题，传统思路需要事先提取好情感词典，而这一步骤，往往需要人工操作才能保证准确率，换句话说，做这个事情的人，不仅仅要是数据挖掘专家，还需要语言学家，这个背景知识依赖性问题会阻碍着自然语言处理的进步。

点击阅读全文...

毫无疑问，数据是数据分析的基础，而对于我等平民来说，获取大量数据的方式自然是通过爬虫采集，而对于笔者来说，写爬虫最自然的方式就是用Python写了。短短几行代码，就可以完成一个实用的爬虫，多清爽。（请参考：《记录一次爬取淘宝/天猫评论数据的过程》）

爬虫要住在哪里？

接下来的一个问题是，这个爬虫放到哪里运行？为了爬取每天更新的数据，往往需要每天都要运行一次爬虫，特别地，是在某个点定时运行。这样的话，老挂在自己的电脑运行是不大现实，因为自己的电脑总有关机的时候。也许有读者会想到放在云服务器里边，这是个方法，但是需要额外的成本。受到小虾大神的启发，我开始想把它放到路由器里边运行，某些比较好的路由器是可以外接U盘，且可以刷open-wrt系统的（一个Linux内核的路由器系统，可以像普通Linux那样装Python）。这对我来说是一种很吸引人的做法，但是我对Linux环境下的编译并不熟悉，尤其是路由器环境下的操作；另外路由器配置很低，一般都只是16M闪存、64M内存，如果没有耐心，那么是很难受得了的。

点击阅读全文...

本文以尽可能清晰、简明的方式来介绍了一阶偏微分方程的特征线法。个人认为这是偏微分方程理论中较为简单但事实上又容易让人含糊的一部分内容，因此尝试以自己的文字来做一番介绍。当然，更准确来说其实是笔者自己的备忘。

拟线性情形

一般步骤

考虑偏微分方程
$$\begin{equation}\boldsymbol{\alpha}(\boldsymbol{x},u) \cdot \frac{\partial}{\partial \boldsymbol{x}} u = \beta(\boldsymbol{x},u)\end{equation}$$
其中$\boldsymbol{\alpha}$是一个$n$维向量函数，$\beta$是一个标量函数，$\cdot$是向量的点积，$u\equiv u(\boldsymbol{x})$是$n$元函数，$\boldsymbol{x}$是它的自变量。

点击阅读全文...