变分自编码器(八):估计样本概率密度
By 苏剑林 | 2021-12-09 | 75171位读者 | 引用在本系列的前面几篇文章中,我们已经从多个角度来理解了VAE,一般来说,用VAE是为了得到一个生成模型,或者是做更好的编码模型,这都是VAE的常规用途。但除了这些常规应用外,还有一些“小众需求”,比如用来估计x的概率密度,这在做压缩的时候通常会用到。
本文就从估计概率密度的角度来了解和推导一下VAE模型。
两个问题
所谓估计概率密度,就是在已知样本x1,x2,⋯,xN∼˜p(x)的情况下,用一个待定的概率密度簇qθ(x)去拟合这批样本,拟合的目标一般是最小化负对数似然:
Ex∼˜p(x)[−logqθ(x)]=−1NN∑i=1logqθ(xi)
指数梯度下降 + 元学习 = 自适应学习率
By 苏剑林 | 2022-03-03 | 35984位读者 | 引用前两天刷到了Google的一篇论文《Step-size Adaptation Using Exponentiated Gradient Updates》,在其中学到了一些新的概念,所以在此记录分享一下。主要的内容有两个,一是非负优化的指数梯度下降,二是基于元学习思想的学习率调整算法,两者都颇有意思,有兴趣的读者也可以了解一下。
指数梯度下降
梯度下降大家可能听说得多了,指的是对于无约束函数\mathcal{L}(\boldsymbol{\theta})的最小化,我们用如下格式进行更新:
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t - \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\end{equation}
其中\eta是学习率。然而很多任务并非总是无约束的,对于最简单的非负约束,我们可以改为如下格式更新:
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t \odot \exp\left(- \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\right)\label{eq:egd}\end{equation}
这里的\odot是逐位对应相乘(Hadamard积)。容易看到,只要初始化的\boldsymbol{\theta}_0是非负的,那么在整个更新过程中\boldsymbol{\theta}_t都会保持非负,这就是用于非负约束优化的“指数梯度下降”。
你的语言模型有没有“无法预测的词”?
By 苏剑林 | 2022-04-20 | 24153位读者 | 引用众所周知,分类模型通常都是先得到编码向量,然后接一个Dense层预测每个类别的概率,而预测时则是输出概率最大的类别。但大家是否想过这样一种可能:训练好的分类模型可能存在“无法预测的类别”,即不管输入是什么,都不可能预测出某个类别k,类别k永远不可能成为概率最大的那个。
当然,这种情况一般只出现在类别数远远超过编码向量维度的场景,常规的分类问题很少这么极端的。然而,我们知道语言模型本质上也是一个分类模型,它的类别数也就是词表的总大小,往往是远超过向量维度的,那么我们的语言模型是否有“无法预测的词”?(只考虑Greedy解码)
是否存在
ACL2022的论文《Low-Rank Softmax Can Have Unargmaxable Classes in Theory but Rarely in Practice》首先探究了这个问题,正如其标题所言,答案是“理论上存在但实际出现概率很小”。
logsumexp运算的几个不等式
By 苏剑林 | 2022-05-10 | 26788位读者 | 引用\text{logsumexp}是机器学习经常遇到的运算,尤其是交叉熵的相关实现和推导中都会经常出现,同时它还是\max的光滑近似(参考《寻求一个光滑的最大值函数》)。设x=(x_1,x_2,\cdots,x_n),\text{logsumexp}定义为
\begin{equation}\text{logsumexp}(x)=\log\sum_{i=1}^n e^{x_i}\end{equation}
本文来介绍\text{logsumexp}的几个在理论推导中可能用得到的不等式。
基本界
记x_{\max} = \max(x_1,x_2,\cdots,x_n),那么显然有
\begin{equation}e^{x_{\max}} < \sum_{i=1}^n e^{x_i} \leq \sum_{i=1}^n e^{x_{\max}} = ne^{x_{\max}}\end{equation}
各端取对数即得
\begin{equation}x_{\max} < \text{logsumexp}(x) \leq x_{\max} + \log n\end{equation}
当BERT-whitening引入超参数:总有一款适合你
By 苏剑林 | 2022-05-18 | 46941位读者 | 引用在《你可能不需要BERT-flow:一个线性变换媲美BERT-flow》中,笔者提出了BERT-whitening,验证了一个线性变换就能媲美当时的SOTA方法BERT-flow。此外,BERT-whitening还可以对句向量进行降维,带来更低的内存占用和更快的检索速度。然而,在《无监督语义相似度哪家强?我们做了个比较全面的评测》中我们也发现,whitening操作并非总能带来提升,有些模型本身就很贴合任务(如经过有监督训练的SimBERT),那么额外的whitening操作往往会降低效果。
为了弥补这个不足,本文提出往BERT-whitening中引入了两个超参数,通过调节这两个超参数,我们几乎可以总是获得“降维不掉点”的结果。换句话说,即便是原来加上whitening后效果会下降的任务,如今也有机会在降维的同时获得相近甚至更好的效果了。
方法概要
目前BERT-whitening的流程是:
\begin{equation}\begin{aligned}
\tilde{\boldsymbol{x}}_i =&\, (\boldsymbol{x}_i - \boldsymbol{\mu})\boldsymbol{U}\boldsymbol{\Lambda}^{-1/2} \\
\boldsymbol{\mu} =&\, \frac{1}{N}\sum\limits_{i=1}^N \boldsymbol{x}_i \\
\boldsymbol{\Sigma} =&\, \frac{1}{N}\sum\limits_{i=1}^N (\boldsymbol{x}_i - \boldsymbol{\mu})^{\top}(\boldsymbol{x}_i - \boldsymbol{\mu}) = \boldsymbol{U}\boldsymbol{\Lambda}\boldsymbol{U}^{\top} \,\,(\text{SVD分解})
\end{aligned}\end{equation}
如何训练你的准确率?
By 苏剑林 | 2022-06-01 | 31551位读者 | 引用最近Arxiv上的一篇论文《EXACT: How to Train Your Accuracy》引起了笔者的兴趣,顾名思义这是介绍如何直接以准确率为训练目标来训练模型的。正好笔者之前也对此有过一些分析,如《函数光滑化杂谈:不可导函数的可导逼近》、《再谈类别不平衡问题:调节权重与魔改Loss的对比联系》等, 所以带着之前的研究经验很快完成了论文的阅读,写下了这篇总结,并附上了最近关于这个主题的一些新思考。
失实的例子
论文开头指出,我们平时用的分类损失函数是交叉熵或者像SVM中的Hinge Loss,这两个损失均不能很好地拟合最终的评价指标准确率。为了说明这一点,论文举了一个很简单的例子:假设数据只有\{(-0.25,-1),(0,-1),(0.25,,1)\}三个点,-1和1分别代表负类和正类,待拟合模型是f(x)=x-b,b是参数,我们希望通过\text{sign}(f(x))来预测类别。如果用“sigmoid + 交叉熵”,那么损失函数就是-\log \frac{1}{1+e^{-l \cdot f(x)}},(x,l)代表一对标签数据;如果用Hinge Loss,则是\max(0, 1 - l\cdot f(x))。
生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪
By 苏剑林 | 2022-07-19 | 181989位读者 | 引用到目前为止,笔者给出了生成扩散模型DDPM的两种推导,分别是《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中的通俗类比方案和《生成扩散模型漫谈(二):DDPM = 自回归式VAE》中的变分自编码器方案。两种方案可谓各有特点,前者更为直白易懂,但无法做更多的理论延伸和定量理解,后者理论分析上更加完备一些,但稍显形式化,启发性不足。
在这篇文章中,我们再分享DDPM的一种推导,它主要利用到了贝叶斯定理来简化计算,整个过程的“推敲”味道颇浓,很有启发性。不仅如此,它还跟我们后面将要介绍的DDIM模型有着紧密的联系。
“维度灾难”之Hubness现象浅析
By 苏剑林 | 2022-06-28 | 46431位读者 | 引用这几天读到论文《Exploring and Exploiting Hubness Priors for High-Quality GAN Latent Sampling》,了解到了一个新的名词“Hubness现象”,说的是高维空间中的一种聚集效应,本质上是“维度灾难”的体现之一。论文借助Hubness的概念得到了一个提升GAN模型生成质量的方案,看起来还蛮有意思。所以笔者就顺便去学习了一下Hubness现象的相关内容,记录在此,供大家参考。
坍缩的球
“维度灾难”是一个很宽泛的概念,所有在高维空间中与相应的二维、三维空间版本出入很大的结论,都可以称之为“维度灾难”,比如《n维空间下两个随机向量的夹角分布》中介绍的“高维空间中任何两个向量几乎都是垂直的”。其中,有不少维度灾难现象有着同一个源头——“高维空间单位球与其外切正方体的体积之比逐渐坍缩至0”,包括本文的主题“Hubness现象”亦是如此。







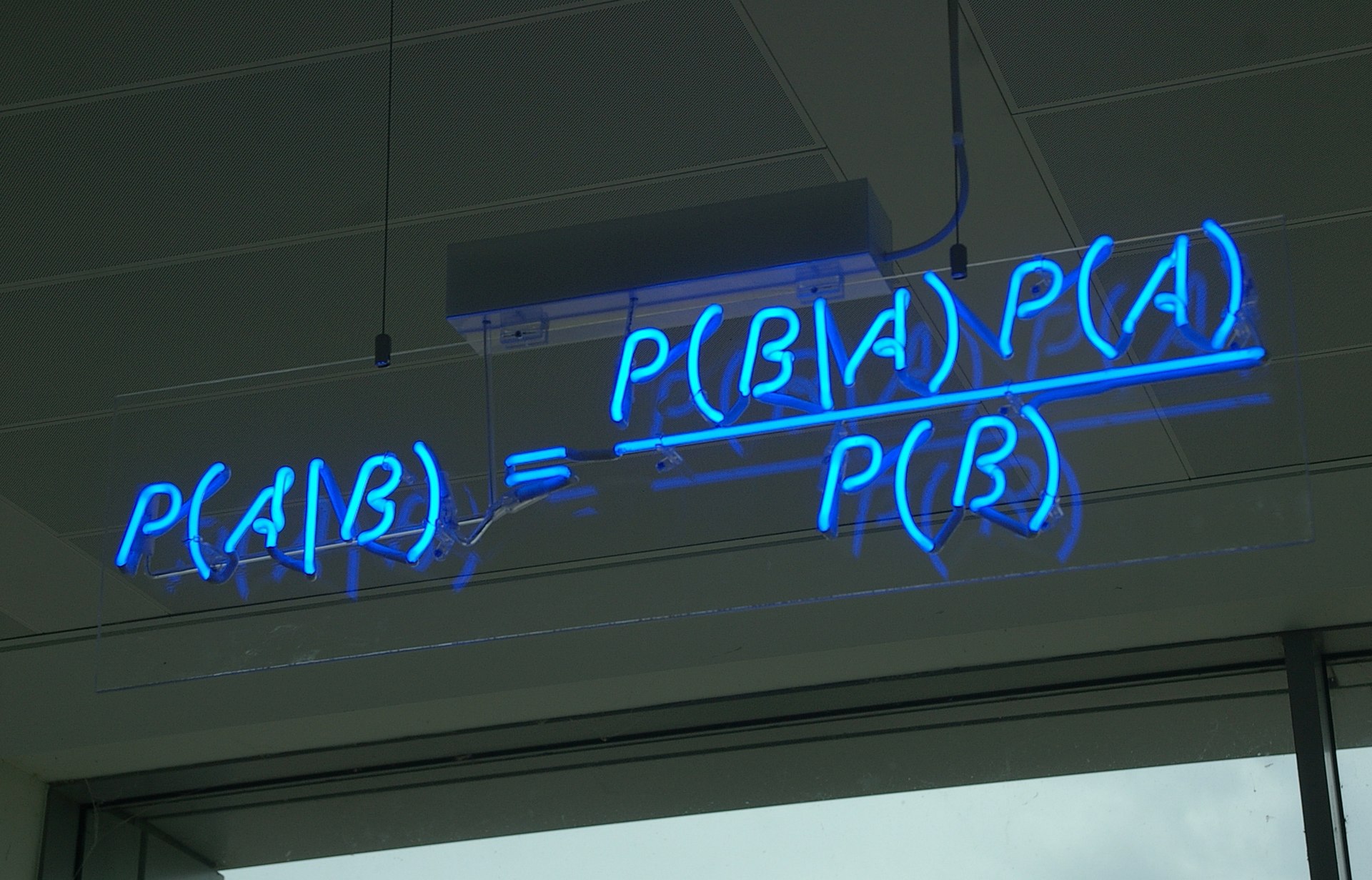

最近评论