5
Dec
万能的seq2seq：基于seq2seq的阅读理解问答
By 苏剑林 | 2019-12-05 | 89309位读者 | 引用今天给bert4keras新增加了一个例子：阅读理解式问答（task_reading_comprehension_by_seq2seq.py），语料跟之前一样，都是用WebQA和SogouQA，最终的得分在0.77左右（单模型，没精调）。
用seq2seq做阅读理解的模型图示
方法简述
由于这次主要目的是给bert4keras增加demo，因此效率就不是主要关心的目标了。这次的目标主要是通用性和易用性，所以用了最万能的方案——seq2seq来实现做阅读理解。
用seq2seq做的话，基本不用怎么关心模型设计，只要把篇章和问题拼接起来，然后预测答案就行了。此外，seq2seq的方案还自然地包括了判断篇章有无答案的方法，以及自然地导出一种多篇章投票的思路。总而言之，不考虑效率的话，seq2seq做阅读理解是一种相当优雅的方案。
这次实现seq2seq还是用UNILM的方案，如果还不了解的读者，可以先阅读《从语言模型到Seq2Seq：Transformer如戏，全靠Mask》了解相应内容。
11
May
AdaX优化器浅析（附开源实现）
By 苏剑林 | 2020-05-11 | 34393位读者 | 引用这篇文章简单介绍一个叫做AdaX的优化器，来自《AdaX: Adaptive Gradient Descent with Exponential Long Term Memory》。介绍这个优化器的原因是它再次印证了之前在《AdaFactor优化器浅析（附开源实现）》一文中提到的一个结论，两篇文章可以对比着阅读。
Adam & AdaX
AdaX的更新格式是
\begin{equation}\left\{\begin{aligned}&g_t = \nabla_{\theta} L(\theta_t)\\
&m_t = \beta_1 m_{t-1} + \left(1 - \beta_1\right) g_t\\
&v_t = (1 + \beta_2) v_{t-1} + \beta_2 g_t^2\\
&\hat{v}_t = v_t\left/\left(\left(1 + \beta_2\right)^t - 1\right)\right.\\
&\theta_t = \theta_{t-1} - \alpha_t m_t\left/\sqrt{\hat{v}_t + \epsilon}\right.
\end{aligned}\right.\end{equation}
其中$\beta_2$的默认值是$0.0001$。对了，顺便附上自己的Keras实现：https://github.com/bojone/adax
11
Dec
输入梯度惩罚与参数梯度惩罚的一个不等式
By 苏剑林 | 2021-12-11 | 23579位读者 | 引用在本博客中，已经多次讨论过梯度惩罚相关内容了。从形式上来看，梯度惩罚项分为两种，一种是关于输入的梯度惩罚$\Vert\nabla_{\boldsymbol{x}} f(\boldsymbol{x};\boldsymbol{\theta})\Vert^2$，在《对抗训练浅谈：意义、方法和思考（附Keras实现）》、《泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练》等文章中我们讨论过，另一种则是关于参数的梯度惩罚$\Vert\nabla_{\boldsymbol{\theta}} f(\boldsymbol{x};\boldsymbol{\theta})\Vert^2$，在《从动力学角度看优化算法（五）：为什么学习率不宜过小？》、《我们真的需要把训练集的损失降低到零吗？》等文章我们讨论过。
在相关文章中，两种梯度惩罚都声称有着提高模型泛化性能的能力，那么两者有没有什么联系呢？笔者从Google最近的一篇论文《The Geometric Occam's Razor Implicit in Deep Learning》学习到了两者的一个不等式，算是部分地回答了这个问题，并且感觉以后可能用得上，在此做个笔记。
最终结果
假设有一个$l$层的MLP模型，记为
\begin{equation}\boldsymbol{h}^{(t+1)} = g^{(t)}(\boldsymbol{W}^{(t)}\boldsymbol{h}^{(t)}+\boldsymbol{b}^{(t)})\end{equation}
其中$g^{(t)}$是当前层的激活函数，$t\in\{1,2,\cdots,l\}$，并记$\boldsymbol{h}^{(1)}$为$\boldsymbol{x}$，即模型的原始输入，为了方便后面的推导，我们记$\boldsymbol{z}^{(t+1)}=\boldsymbol{W}^{(t)}\boldsymbol{h}^{(t)}+\boldsymbol{b}^{(t)}$；参数全体为$\boldsymbol{\theta}=\{\boldsymbol{W}^{(1)},\boldsymbol{b}^{(1)},\boldsymbol{W}^{(2)},\boldsymbol{b}^{(2)},\cdots,\boldsymbol{W}^{(l)},\boldsymbol{b}^{(l)}\}$。设$f$是$\boldsymbol{h}^{(l+1)}$的任意标量函数，那么成立不等式
\begin{equation}\Vert\nabla_{\boldsymbol{x}} f\Vert^2\left(\frac{1 + \Vert \boldsymbol{h}^{(1)}\Vert^2}{\Vert\boldsymbol{W}^{(1)}\Vert^2 \Vert\nabla_{\boldsymbol{x}}\boldsymbol{h}^{(1)}\Vert^2}+\cdots+\frac{1 + \Vert \boldsymbol{h}^{(l)}\Vert^2}{\Vert\boldsymbol{W}^{(l)}\Vert^2 \Vert\nabla_{\boldsymbol{x}}\boldsymbol{h}^{(l)}\Vert^2}\right)\leq \Vert\nabla_{\boldsymbol{\theta}} f\Vert^2\label{eq:f}\end{equation}
25
Jan
Efficient GlobalPointer：少点参数，多点效果
By 苏剑林 | 2022-01-25 | 121770位读者 | 引用在《GlobalPointer：用统一的方式处理嵌套和非嵌套NER》中，我们提出了名为“GlobalPointer”的token-pair识别模块，当它用于NER时，能统一处理嵌套和非嵌套任务，并在非嵌套场景有着比CRF更快的速度和不逊色于CRF的效果。换言之，就目前的实验结果来看，至少在NER场景，我们可以放心地将CRF替换为GlobalPointer，而不用担心效果和速度上的损失。
在这篇文章中，我们提出GlobalPointer的一个改进版——Efficient GlobalPointer，它主要针对原GlobalPointer参数利用率不高的问题进行改进，明显降低了GlobalPointer的参数量。更有趣的是，多个任务的实验结果显示，参数量更少的Efficient GlobalPointer反而还取得更好的效果。
大量的参数
这里简单回顾一下GlobalPointer，详细介绍则请读者阅读《GlobalPointer：用统一的方式处理嵌套和非嵌套NER》。简单来说，GlobalPointer是基于内积的token-pair识别模块，它可以用于NER场景，因为对于NER来说我们只需要把每一类实体的“(首, 尾)”这样的token-pair识别出来就行了。
21
Feb
GPLinker：基于GlobalPointer的事件联合抽取
By 苏剑林 | 2022-02-21 | 77638位读者 | 引用大约两年前，笔者在百度的“2020语言与智能技术竞赛”中首次接触到了事件抽取任务，并在文章《bert4keras在手，baseline我有：百度LIC2020》中分享了一个转化为BERT+CRF做NER的简单baseline。不过，当时的baseline更像是一个用来凑数的半成品，算不上一个完整的事件抽取模型。而这两年来，关系抽取的模型层见迭出，SOTA一个接一个，但事件抽取似乎没有多亮眼的设计。
最近笔者重新尝试了事件抽取任务，在之前的关系抽取模型GPLinker的基础上，结合完全子图搜索，设计一个比较简单但相对完备的事件联合抽取模型，依然称之为GPLinker，在此请大家点评一番。
任务简介
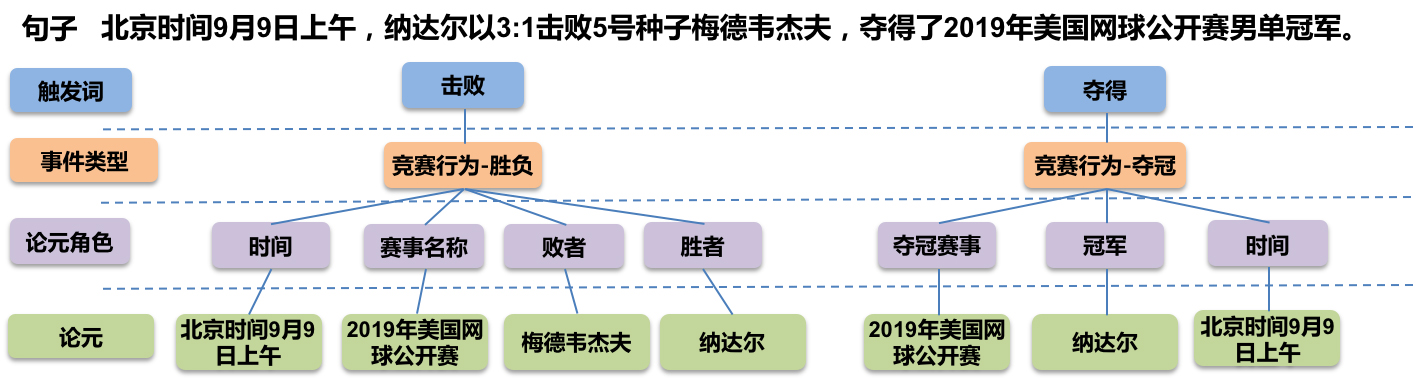
事件抽取是一个比较综合的任务。一个标准的事件抽取样本如下：
标准的事件抽取样本（图片来自百度DuEE的GitHub）
7
May
多标签“Softmax+交叉熵”的软标签版本
By 苏剑林 | 2022-05-07 | 50126位读者 | 引用（注：本文的相关内容已整理成论文《ZLPR: A Novel Loss for Multi-label Classification》，如需引用可以直接引用英文论文，谢谢。）
在《将“Softmax+交叉熵”推广到多标签分类问题》中，我们提出了一个用于多标签分类的损失函数：
\begin{equation}\log \left(1 + \sum\limits_{i\in\Omega_{neg}} e^{s_i}\right) + \log \left(1 + \sum\limits_{j\in\Omega_{pos}} e^{-s_j}\right)\label{eq:original}\end{equation}
这个损失函数有着单标签分类中“Softmax+交叉熵”的优点，即便在正负类不平衡的依然能够有效工作。但从这个损失函数的形式我们可以看到，它只适用于“硬标签”，这就意味着label smoothing、mixup等技巧就没法用了。本文则尝试解决这个问题，提出上述损失函数的一个软标签版本。
巧妙联系
多标签分类的经典方案就是转化为多个二分类问题，即每个类别用sigmoid函数$\sigma(x)=1/(1+e^{-x})$激活，然后各自用二分类交叉熵损失。当正负类别极其不平衡时，这种做法的表现通常会比较糟糕，而相比之下损失$\eqref{eq:original}$通常是一个更优的选择。
27
Jun
哈哈，我的“《圣经》”到了
By 苏剑林 | 2013-06-27 | 55689位读者 | 引用
12
Jul
最近评论