从动力学角度看优化算法(三):一个更整体的视角
By 苏剑林 | 2019-01-08 | 57832位读者 | 引用构造一个显式的、总是可逆的矩阵
By 苏剑林 | 2019-03-01 | 41830位读者 | 引用从《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》一文我们得到矩阵$\exp(\boldsymbol{A})$总是可逆的,它的逆就是$\exp(-\boldsymbol{A})$。问题是$\exp(\boldsymbol{A})$只是一个理论定义,单纯这样写没有什么价值,因为它要把每个$\boldsymbol{A}^n$都算出来。
有没有什么具体的例子呢?有,本文来构造一个显式的、总是可逆的矩阵。
其实思路非常简单,假设$\boldsymbol{x},\boldsymbol{y}$是两个$k$维列向量,那么$\boldsymbol{x}\boldsymbol{y}^{\top}$就是一个$k\times k$的矩阵,我们就来考虑
\begin{equation}\begin{aligned}\exp\left(\boldsymbol{x}\boldsymbol{y}^{\top}\right)=&\sum_{n=0}^{\infty}\frac{\left(\boldsymbol{x}\boldsymbol{y}^{\top}\right)^n}{n!}\\
=&\boldsymbol{I}+\boldsymbol{x}\boldsymbol{y}^{\top}+\frac{\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}}{2}+\frac{\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}}{6}+\dots\end{aligned}\end{equation}
从DCGAN到SELF-MOD:GAN的模型架构发展一览
By 苏剑林 | 2019-04-19 | 79055位读者 | 引用事实上,O-GAN的发现,已经达到了我对GAN的理想追求,使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向,比如NLP中还没做过的任务,又比如图神经网络,又或者其他有趣的东西。
不过,在此之前,我想把之前的GAN的学习结果都记录下来。
这篇文章中,我们来梳理一下GAN的架构发展情况,当然主要的是生成器的发展,判别器一直以来的变动都不大。还有,本文介绍的是GAN在图像方面的模型架构发展,跟NLP的SeqGAN没什么关系。
此外,关于GAN的基本科普,本文就不再赘述了。
Self-Orthogonality Module:一个即插即用的核正交化模块
By 苏剑林 | 2020-01-12 | 52829位读者 | 引用前些天刷Arxiv看到新文章《Self-Orthogonality Module: A Network Architecture Plug-in for Learning Orthogonal Filters》(下面简称“原论文”),看上去似乎有点意思,于是阅读了一番,读完确实有些收获,在此记录分享一下。
给全连接或者卷积模型的核加上带有正交化倾向的正则项,是不少模型的需求,比如大名鼎鼎的BigGAN就加入了类似的正则项。而这篇论文则引入了一个新的正则项,笔者认为整个分析过程颇为有趣,可以一读。
为什么希望正交?
在开始之前,我们先约定:本文所出现的所有一维向量都代表列向量。那么,现在假设有一个$d$维的输入样本$\boldsymbol{x}\in \mathbb{R}^d$,经过全连接或卷积层时,其核心运算就是:
\begin{equation}\boldsymbol{y}^{\top}=\boldsymbol{x}^{\top}\boldsymbol{W},\quad \boldsymbol{W}\triangleq (\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k)\label{eq:k}\end{equation}
其中$\boldsymbol{W}\in \mathbb{R}^{d\times k}$是一个矩阵,它就被称“核”(全连接核/卷积核),而$\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k\in \mathbb{R}^{d}$是该矩阵的各个列向量。
函数光滑化杂谈:不可导函数的可导逼近
By 苏剑林 | 2019-05-20 | 121521位读者 | 引用一般来说,神经网络处理的东西都是连续的浮点数,标准的输出也是连续型的数字。但实际问题中,我们很多时候都需要一个离散的结果,比如分类问题中我们希望输出正确的类别,“类别”是离散的,“类别的概率”才是连续的;又比如我们很多任务的评测指标实际上都是离散的,比如分类问题的正确率和F1、机器翻译中的BLEU,等等。
还是以分类问题为例,常见的评测指标是正确率,而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联,但它们不是绝对的单调相关关系。换句话说,交叉熵下降了,正确率不一定上升。显然,如果能用正确率的相反数做损失函数,那是最理想的,但正确率是不可导的(涉及到$\text{argmax}$等操作),所以没法直接用。
这时候一般有两种解决方案;一是动用强化学习,将正确率设为奖励函数,这是“用牛刀杀鸡”的方案;另外一种是试图给正确率找一个光滑可导的近似公式。本文就来探讨一下常见的不可导函数的光滑近似,有时候我们称之为“光滑化”,有时候我们也称之为“软化”。
max
后面谈到的大部分内容,基础点就是$\max$操作的光滑近似,我们有:
\begin{equation}\max(x_1,x_2,\dots,x_n) = \lim_{K\to +\infty}\frac{1}{K}\log\left(\sum_{i=1}^n e^{K x_i}\right)\end{equation}
“让Keras更酷一些!”:层中层与mask
By 苏剑林 | 2019-07-16 | 145476位读者 | 引用这一篇“让Keras更酷一些!”将和读者分享两部分内容:第一部分是“层中层”,顾名思义,是在Keras中自定义层的时候,重用已有的层,这将大大减少自定义层的代码量;另外一部分就是应读者所求,介绍一下序列模型中的mask原理和方法。
层中层
在《“让Keras更酷一些!”:精巧的层与花式的回调》一文中我们已经介绍过Keras自定义层的基本方法,其核心步骤是定义build和call两个函数,其中build负责创建可训练的权重,而call则定义具体的运算。
拒绝重复劳动
经常用到自定义层的读者可能会感觉到,在自定义层的时候我们经常在重复劳动,比如我们想要增加一个线性变换,那就要在build中增加一个kernel和bias变量(还要自定义变量的初始化、正则化等),然后在call里边用K.dot来执行,有时候还需要考虑维度对齐的问题,步骤比较繁琐。但事实上,一个线性变换其实就是一个不加激活函数的Dense层罢了,如果在自定义层时能重用已有的层,那显然就可以大大节省代码量了。
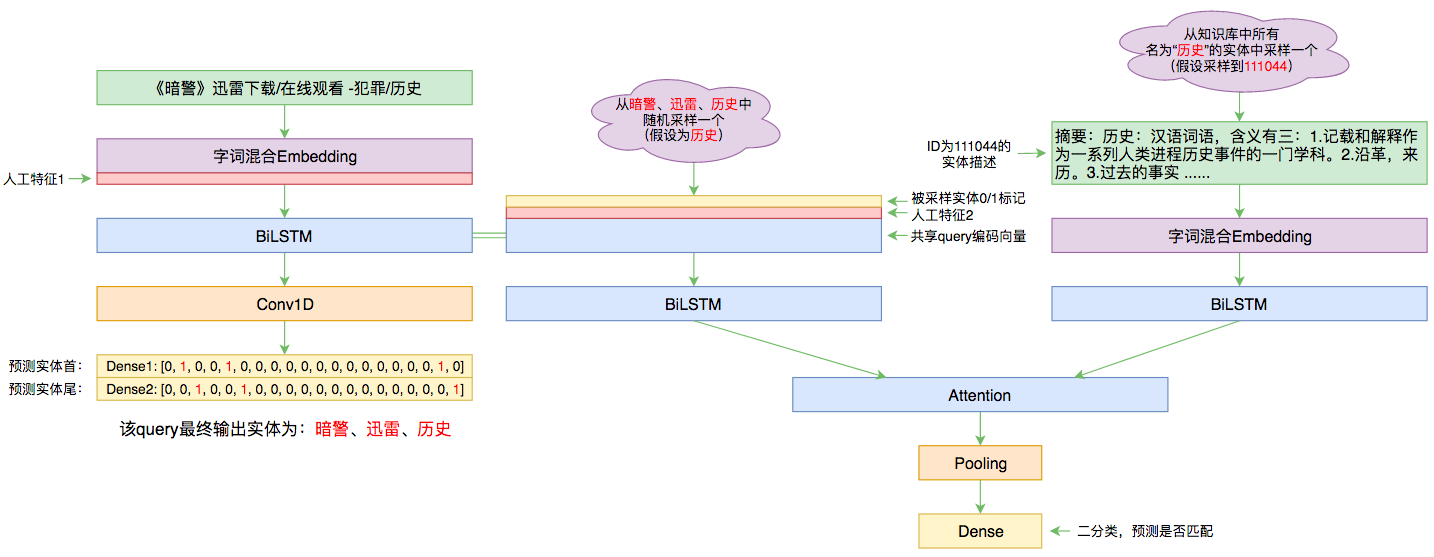
百度实体链接比赛后记:行为建模和实体链接
By 苏剑林 | 2019-09-03 | 83706位读者 | 引用前几个月曾参加了百度的实体链接比赛,这是CCKS2019的评测任务之一,官方称之为“实体链指”,比赛于前几个星期完全结束。笔者最终的F1是0.78左右(冠军是0.80),排在第14名,成绩并不突出(唯一的特色是模型很轻量级,GTX1060都可以轻松跑起来),所以本文只是纯粹的记录过程,大牛们请一笑置之~
赛题介绍
所谓实体链接,主要指的是在已有一个知识库的情况下,预测输入query的某个实体对应知识库id。也就是说,知识库里边记录了很多实体,对于同一个名字的实体可能会有多个解释,每个解释用一个唯一id编号,我们要做的就是预测query中的实体究竟对应哪一个解释(id)。这是基于知识图谱的问答系统的必要步骤。
从去噪自编码器到生成模型
By 苏剑林 | 2019-10-31 | 106678位读者 | 引用在我看来,几大顶会之中,ICLR的论文通常是最有意思的,因为它们的选题和风格基本上都比较轻松活泼、天马行空,让人有脑洞大开之感。所以,ICLR 2020的投稿论文列表出来之后,我也抽时间粗略过了一下这些论文,确实发现了不少有意思的工作。
其中,我发现了两篇利用去噪自编码器的思想做生成模型的论文,分别是《Learning Generative Models using Denoising Density Estimators》和《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》。由于常规做生成模型的思路我基本都有所了解,所以这种“别具一格”的思路就引起了我的兴趣。细读之下,发现两者的出发点是一致的,但是具体做法又有所不同,最终的落脚点又是一样的,颇有“一题多解”的美妙,遂将这两篇论文放在一起,对比分析一翻。










最近评论