让研究人员绞尽脑汁的Transformer位置编码
By 苏剑林 | 2021-02-03 | 204726位读者 | 引用不同于RNN、CNN等模型,对于Transformer模型来说,位置编码的加入是必不可少的,因为纯粹的Attention模块是无法捕捉输入顺序的,即无法区分不同位置的Token。为此我们大体有两个选择:1、想办法将位置信息融入到输入中,这构成了绝对位置编码的一般做法;2、想办法微调一下Attention结构,使得它有能力分辨不同位置的Token,这构成了相对位置编码的一般做法。
虽然说起来主要就是绝对位置编码和相对位置编码两大类,但每一类其实又能衍生出各种各样的变种,为此研究人员可算是煞费苦心、绞尽脑汁了,此外还有一些不按套路出牌的位置编码。本文就让我们来欣赏一下研究人员为了更好地表达位置信息所构建出来的“八仙过海,各显神通”般的编码方案。
绝对位置编码
形式上来看,绝对位置编码是相对简单的一种方案,但即便如此,也不妨碍各路研究人员的奇思妙想,也有不少的变种。一般来说,绝对位置编码会加到输入中:在输入的第$k$个向量$\boldsymbol{x}_k$中加入位置向量$\boldsymbol{p}_k$变为$\boldsymbol{x}_k + \boldsymbol{p}_k$,其中$\boldsymbol{p}_k$只依赖于位置编号$k$。
两个多元正态分布的KL散度、巴氏距离和W距离
By 苏剑林 | 2021-07-08 | 110267位读者 | 引用正态分布是最常见的连续型概率分布之一。它是给定均值和协方差后的最大熵分布(参考《“熵”不起:从熵、最大熵原理到最大熵模型(二)》),也可以看作任意连续型分布的二阶近似,它的地位就相当于一般函数的线性近似。从这个角度来看,正态分布算得上是最简单的连续型分布了。也正因为简单,所以对于很多估计量来说,它都能写出解析解来。
本文主要来计算两个多元正态分布的几种度量,包括KL散度、巴氏距离和W距离,它们都有显式解析解。
正态分布
这里简单回顾一下正态分布的一些基础知识。注意,仅仅是回顾,这还不足以作为正态分布的入门教程。
概率密度
正态分布,也即高斯分布,是定义在$\mathbb{R}^n$上的连续型概率分布,其概率密度函数为
\begin{equation}p(\boldsymbol{x})=\frac{1}{\sqrt{(2\pi)^n \det(\boldsymbol{\Sigma})}}\exp\left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}\end{equation}
关于WhiteningBERT原创性的疑问和沟通
By 苏剑林 | 2021-10-09 | 67695位读者 | 引用在文章《你可能不需要BERT-flow:一个线性变换媲美BERT-flow》中,笔者受到BERT-flow的启发,提出了一种名为BERT-whitening的替代方案,它比BERT-flow更简单,但多数数据集下能取得相近甚至更好的效果,此外它还可以用于对句向量降维以提高检索速度。后来,笔者跟几位合作者一起补充了BERT-whitening的实验,并将其写成了英文论文《Whitening Sentence Representations for Better Semantics and Faster Retrieval》,在今年3月29日发布在Arxiv上。
然而,大约一周后,一篇名为《WhiteningBERT: An Easy Unsupervised Sentence Embedding Approach》的论文 (下面简称WhiteningBERT)出现在Arxiv上,内容跟BERT-whitening高度重合,有读者看到后向我反馈WhiteningBERT抄袭了BERT-whitening。本文跟关心此事的读者汇报一下跟WhiteningBERT的作者之间的沟通结果。
时间节点
首先,回顾一下BERT-whitening的相关时间节点,以帮助大家捋一下事情的发展顺序:
又是Dropout两次!这次它做到了有监督任务的SOTA
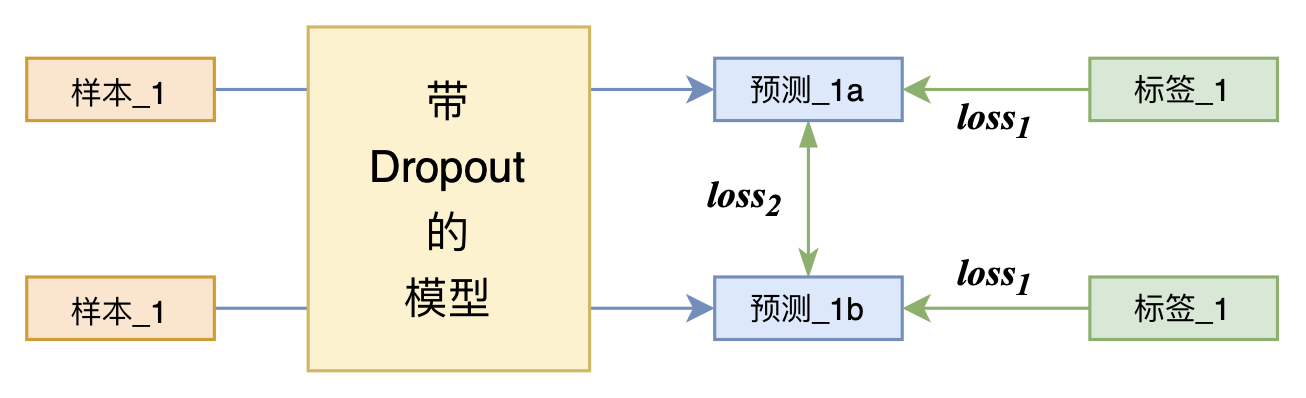
By 苏剑林 | 2021-07-01 | 216914位读者 | 引用关注NLP新进展的读者,想必对四月份发布的SimCSE印象颇深,它通过简单的“Dropout两次”来构造正样本进行对比学习,达到了无监督语义相似度任务的全面SOTA。无独有偶,最近的论文《R-Drop: Regularized Dropout for Neural Networks》提出了R-Drop,它将“Dropout两次”的思想用到了有监督任务中,每个实验结果几乎都取得了明显的提升。此外,笔者在自己的实验还发现,它在半监督任务上也能有不俗的表现。
小小的“Dropout两次”,居然跑出了“五项全能”的感觉,不得不令人惊讶。本文来介绍一下R-Drop,并分享一下笔者对它背后原理的思考。
【搜出来的文本】⋅(四)通过增、删、改来用词造句
By 苏剑林 | 2021-02-25 | 49280位读者 | 引用“用词造句”是小学阶段帮助我们理解和运用词语的一个经典任务,从自然语言处理的角度来看,它是一个句子扩写或者句子补全任务,它其实要求我们具有不定向地进行文本生成的能力。然而,当前主流的语言模型都是单方向生成的(多数是正向的,即从左往右,少数是反向的,即从右往左),但用词造句任务中所给的若干个词未必一定出现在句首或者句末,这导致无法直接用语言模型来完成造句任务。
本文我们将介绍论文《CGMH: Constrained Sentence Generation by Metropolis-Hastings Sampling》,它使用MCMC采样使得单向语言模型也可以做到不定向生成,通过增、删、改操作模拟了人的写作润色过程,从而能无监督地完成用词造句等多种文本生成任务。
问题设置
无监督地进行文本采样,那么直接可以由语言模型来完成,而我们同样要做的,是往这个采样过程中加入一些信号$\boldsymbol{c}$,使得它能生成我们期望的一些文本。在本系列第一篇文章《【搜出来的文本】⋅(一)从文本生成到搜索采样》的“明确目标”一节中,我们就介绍了本系列的指导思想:把我们要寻找的目标量化地写下来,然后最大化它或者从中采样。
让人惊叹的Johnson-Lindenstrauss引理:应用篇
By 苏剑林 | 2021-09-24 | 36714位读者 | 引用上一篇文章中,我们比较详细地介绍了Johnson-Lindenstrauss引理(JL引理)的理论推导,这一篇我们来关注它的应用。
作为一个内容上本身就跟降维相关的结论,JL引理最基本的自然就是作为一个降维方法来用。但除了这个直接应用外,很多看似不相关的算法,比如局部敏感哈希(LSH)、随机SVD等,本质上也依赖于JL引理。此外,对于机器学习模型来说,JL引理通常还能为我们的维度选择提供一些理论解释。
降维的工具
JL引理提供了一个非常简单直接的“随机投影”降维思路:
给定$N$个向量$v_1,v_2,\cdots,v_N\in\mathbb{R}^m$,如果想要将它降到$n$维,那么只需要从$\mathcal{N}(0,1/n)$中采样一个$n\times m$矩阵$A$,然后$Av_1,Av_2,\cdots,Av_N$就是降维后的结果。
Transformer升级之路:1、Sinusoidal位置编码追根溯源
By 苏剑林 | 2021-03-08 | 140723位读者 | 引用最近笔者做了一些理解和改进Transformer的尝试,得到了一些似乎还有价值的经验和结论,遂开一个专题总结一下,命名为“Transformer升级之路”,既代表理解上的深入,也代表结果上的改进。
作为该专题的第一篇文章,笔者将会介绍自己对Google在《Attention is All You Need》中提出来的Sinusoidal位置编码
\begin{equation}\left\{\begin{aligned}&\boldsymbol{p}_{k,2i}=\sin\Big(k/10000^{2i/d}\Big)\\
&\boldsymbol{p}_{k, 2i+1}=\cos\Big(k/10000^{2i/d}\Big)
\end{aligned}\right.\label{eq:sin}\end{equation}
的新理解,其中$\boldsymbol{p}_{k,2i},\boldsymbol{p}_{k,2i+1}$分别是位置$k$的编码向量的第$2i,2i+1$个分量,$d$是向量维度。
作为位置编码的一个显式解,Google在原论文中对它的描述却寥寥无几,只是简单提及了它可以表达相对位置信息,后来知乎等平台上也出现了一些解读,它的一些特点也逐步为大家所知,但总体而言比较零散。特别是对于“它是怎么想出来的”、“非得要这个形式不可吗”等原理性问题,还没有比较好的答案。
因此,本文主要围绕这些问题展开思考,可能在思考过程中读者会有跟笔者一样的感觉,即越思考越觉得这个设计之精妙漂亮,让人叹服~
WGAN的成功,可能跟Wasserstein距离没啥关系
By 苏剑林 | 2021-03-15 | 55689位读者 | 引用WGAN,即Wasserstein GAN,算是GAN史上一个比较重要的理论突破结果,它将GAN中两个概率分布的度量从f散度改为了Wasserstein距离,从而使得WGAN的训练过程更加稳定,而且生成质量通常也更好。Wasserstein距离跟最优传输相关,属于Integral Probability Metric(IPM)的一种,这类概率度量通常有着更优良的理论性质,因此WGAN的出现也吸引了很多人从最优传输和IPMs的角度来理解和研究GAN模型。
然而,最近Arxiv上的论文《Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)》则指出,尽管WGAN是从Wasserstein GAN推导出来的,但是现在成功的WGAN并没有很好地近似Wasserstein距离,相反如果我们对Wasserstein距离做更好的近似,效果反而会变差。事实上,笔者一直以来也有这个疑惑,即Wasserstein距离本身并没有体现出它能提升GAN效果的必然性,该论文的结论则肯定了该疑惑,所以GAN能成功的原因依然很迷~








最近评论