科学空间|Scientific Spaces

文本相似度有“交互式”和“特征式”两种做法，想必很多读者对此已经不陌生，之前笔者也写过一篇文章《CoSENT（二）：特征式匹配与交互式匹配有多大差距？》来对比两者的效果。总的来说，交互式相似度效果通常会好些，但直接用它来做大规模检索是不现实的，而特征式相似度则有着更快的检索速度，以及稍逊一筹的效果。

因此，如何在保证交互式相似度效果的前提下提高它的检索速度，是学术界一直都有在研究的课题。近日，论文《Efficient Nearest Neighbor Search for Cross-Encoder Models using Matrix Factorization》提出了一份新的答卷：CUR分解。

CUR分解示意图

点击阅读全文...

在《生成扩散模型漫谈（十）：统一扩散模型（理论篇）》中，笔者自称构建了一个统一的模型框架（Unified Diffusion Model，UDM），它允许更一般的扩散方式和数据类型。那么UDM框架究竟能否实现如期目的呢？本文通过一些具体例子来演示其一般性。

框架回顾

首先，UDM通过选择噪声分布$q(\boldsymbol{\varepsilon})$和变换$\boldsymbol{\mathcal{F}}$来构建前向过程
\begin{equation}\boldsymbol{x}_t = \boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon}),\quad \boldsymbol{\varepsilon}\sim q(\boldsymbol{\varepsilon})\end{equation}
然后，通过如下的分解来实现反向过程$\boldsymbol{x}_{t-1}\sim p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的采样
\begin{equation}\hat{\boldsymbol{x}}_0\sim p(\boldsymbol{x}_0|\boldsymbol{x}_t)\quad \& \quad \boldsymbol{x}_{t-1}\sim p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\hat{\boldsymbol{x}}_0)\end{equation}
其中$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$就是用$\boldsymbol{x}_t$预估$\boldsymbol{x}_0$的概率，一般用简单分布$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$来近似建模，训练目标基本上就是$-\log q(\boldsymbol{x}_0|\boldsymbol{x}_t)$或其简单变体。当$\boldsymbol{x}_0$是连续型数据时，$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$一般就取条件正态分布；当$\boldsymbol{x}_0$是离散型数据时，$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$可以选择自回归模型或者非自回归模型。

点击阅读全文...

在《生成扩散模型漫谈（五）：一般框架之SDE篇》中，我们从SDE的角度理解了生成扩散模型，然后在《生成扩散模型漫谈（六）：一般框架之ODE篇》中，我们知道SDE对应的扩散模型中，实际上隐含了一个ODE模型。无独有偶，在《生成扩散模型漫谈（四）：DDIM = 高观点DDPM》中我们也知道原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。

细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。

微分方程

像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。

点击阅读全文...

这几天网上热传了一道“四鸭共半圆”题目：

四鸭共半圆问题

可能有不少读者看到后也尝试做过，就连李永乐老师也专门开了一节课讲这道题（参考《圆形水池四只鸭子在同一个半圆里，概率有多大？》）。就这道题目本身而言，答案并不算困难，可以有很多方法算出来。稍微有难度的是它的推广版本，也就是本文标题所描述的，将鸭子的数目一般化为$n$只，将半圆一般化为圆心角为$\theta$的扇形。更有趣的是，当$\theta \leq \pi$时，依然有比较初等的解法，但是当$\theta > \pi$后，复杂度开始“剧增”...

点击阅读全文...

上周笔者写了《生成扩散模型漫谈（十四）：构建ODE的一般步骤（上）》（当时还没有“上”这个后缀），本以为已经窥见了构建ODE扩散模型的一般规律，结果不久后评论区大神 @gaohuazuo 就给出了一个构建格林函数更高效、更直观的方案，让笔者自愧不如。再联想起之前大神之前在《生成扩散模型漫谈（十二）：“硬刚”扩散ODE》同样也给出了一个关于扩散ODE的精彩描述（间接启发了上一篇博客的结果），大神的洞察力不得不让人叹服。

经过讨论和思考，笔者发现大神的思路本质上就是一阶偏微分方程的特征线法，通过构造特定的向量场保证初值条件，然后通过求解微分方程保证终值条件，同时保证了初值和终值条件，真的非常巧妙！最后，笔者将自己的收获总结成此文，作为上一篇的后续。

前情回顾

简单回顾一下上一篇文章的结果。假设随机变量$\boldsymbol{x}_0\in\mathbb{R}^d$连续地变换成$\boldsymbol{x}_T$，其变化规律服从ODE
\begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\label{eq-ode}\end{equation}

点击阅读全文...

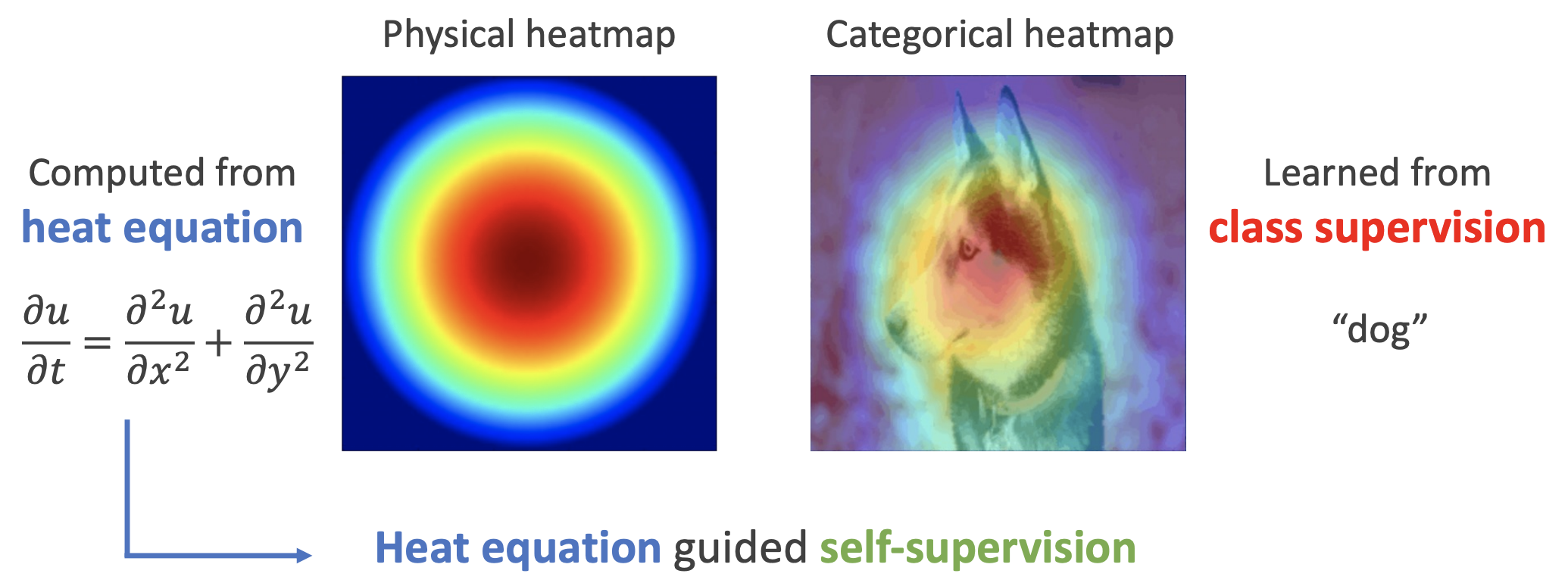
用理论物理来卷机器学习已经不是什么新鲜事了，比如上个月介绍的《生成扩散模型漫谈（十三）：从万有引力到扩散模型》就是经典一例。最近一篇新出的论文《Self-Supervised Learning based on Heat Equation》，顾名思义，用热传导方程来做（图像领域的）自监督学习，引起了笔者的兴趣。这种物理方程如何在机器学习中发挥作用？同样的思路能否迁移到NLP中？让我们一起来读读论文。

基本方程

如下图，左边是物理中热传导方程的解，右端则是CAM、积分梯度等显著性方法得到的归因热力图，可以看到两者有一定的相似之处，于是作者认为热传导方程可以作为好的视觉特征的一个重要先验。

热方程的热力图（左）和视觉模型的热力图（右）

点击阅读全文...

书接上文，在《生成扩散模型漫谈（十三）：从万有引力到扩散模型》中，我们介绍了一个由万有引力启发的、几何意义非常清晰的ODE式生成扩散模型。有的读者看了之后就疑问：似乎“万有引力”并不是唯一的选择，其他形式的力是否可以由同样的物理绘景构建扩散模型？另一方面，该模型在物理上确实很直观，但还欠缺从数学上证明最后确实能学习到数据分布。

本文就尝试从数学角度比较精确地回答“什么样的力场适合构建ODE式生成扩散模型”这个问题。

基础结论

要回答这个问题，需要用到在《生成扩散模型漫谈（十二）：“硬刚”扩散ODE》中我们推导过的一个关于常微分方程对应的分布变化的结论。

考虑$\boldsymbol{x}_t\in\mathbb{R}^d, t\in[0,T]$的一阶（常）微分方程（组）
\begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\label{eq:ode}\end{equation}

点击阅读全文...

在去年的文章《Transformer升级之路：2、博采众长的旋转式位置编码》中，笔者提出了旋转位置编码（RoPE），当时的出发点只是觉得用绝对位置来实现相对位置是一件“很好玩的事情”，并没料到其实际效果还相当不错，并为大家所接受，不得不说这真是一个意外之喜。后来，在《Transformer升级之路：4、二维位置的旋转式位置编码》中，笔者讨论了二维形式的RoPE，并研究了用矩阵指数表示的RoPE的一般解。

既然有了一般解，那么自然就会引出一个问题：我们常用的RoPE，只是一个以二维旋转矩阵为基本单元的分块对角矩阵，如果换成一般解，理论上效果会不会更好呢？本文就来回答这个问题。

指数通解

在《Transformer升级之路：4、二维位置的旋转式位置编码》中，我们将RoPE抽象地定义为任意满足下式的方阵
\begin{equation}\boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n=\boldsymbol{\mathcal{R}}_{n-m}\label{eq:re}\end{equation}

点击阅读全文...