科学空间|Scientific Spaces

The New Calculation Of Lagrangian Point 4,5

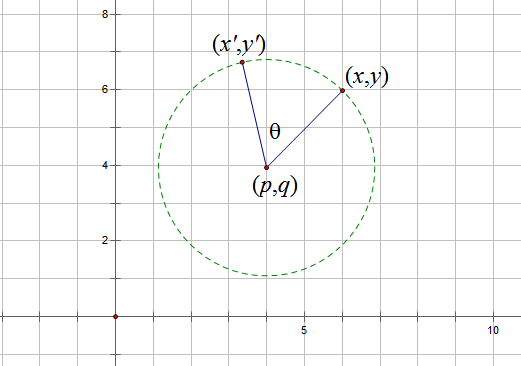
上一回我们已经求出了拉格朗日点L1,L2,L3，并且希望能够求出L4,L5两个点。由于L4,L5与“地球-太阳”连线已经不共线了，所以前边的方法貌似不能够用了。为了得到一个通用的定义，我们可以采用以下方法来描述拉格朗日点：位于拉格朗日点的天体，它与太阳的连线以及地球与太阳的连线所组成的角的大小是恒定的。（这里为了方便，采用了地日系的拉格朗日点来描述，对于一般的三体问题是一样的）

对于L4,L5来说，我们或许可以设置一个新的向量来描述这两点的向径（如$\vec{R}$）。当我们这样做后，很快就会发现这样会令我们的计算走向死胡同。因为我们发现：已知两个向量的夹角和其中一个向量，我们很难把另一个向量用已知向量的式子表达出来。不能做到这一点，就不能找出$\vec{R}$与$\vec{r}$的关系，就无法联立方程求解。难道，我们这一条路走到尽头了吗？一开始BoJone也冥思苦想不得头绪，但是...

点击阅读全文...

坐标旋转

如图，坐标(x,y)绕点(p,q)逆时针旋转θ角后得到坐标(x',y')，求x',y'关于x,y的表达式。

点击阅读全文...

当我们在使用向量进行几何、物理研究的时候，是否曾经想到：向量竟然起源于“数”？

当向量还没有发展起来的时候（虽然“有方向有大小的量”很早就被人们认识），复数已经得到了认可并且有了初步应用。当我们把复数跟向量联系起来时，我们也许会认为，因为复平面表示的复数运算与向量有着相似之处，才把复数跟几何联系起来。然而事实却相反，向量是从对复数乃至一种称为“四元数”的东西的研究中逐渐分离出来的。换句话说，历史中出现过“四元数”与向量分别研究几何的阶段，麦克斯韦(Maxwell) 将四元 数的数量部分和矢量部分分开，作为 实 体处理，作了大量的矢量分析。三维矢量分析的建立，及同四元数的正式分裂是18世纪80年代由Gibbs和Heaviside独立完成的。矢量代数被推广到矢量函数和矢量微积分，由此开始了四元数和矢量分析的争论，最终矢量分析占了上风。因而“四元数”渐渐离开了教科书。不过，“四元数”的一些特殊而巧妙的应用，仍然使我们不至于忘记它。

点击阅读全文...

之前曾经得到过一条计算夏至精确时间的公式，现在检验一下（之前推导是根据了2009年的数据）

公元Y年的夏至日期为该年的6月
$$21.9938+0.2422Y-\lfloor Y/4 \rfloor-\lfloor Y/400 \rfloor+\lfloor Y/100 \rfloor$$
其中$\lfloor x \rfloor$表示整数部分。

点击阅读全文...

关于行星留的周期的计算，我们之前已经讨论过这个问题，利用的是微积分的方法。也许不少还没有高数基础的朋友会感到很头晕，因此在这里给出一个从几何方面讨论的推导。

关于留，很多人认为就是行星相对于地球的速度为0的时刻，其实这个说法稍欠准确，严格来讲应该要将速度改为“角速度”或“切向速度”（天文的切向就是指与视线方向垂直的方向）。实际的运动中，没有哪一瞬间行星相对于地球的运动速度是为0的。根据这句话，我们可以作出下面的图（依旧只考虑正圆运动）：

行星留-运动分析

点击阅读全文...

首先我们考虑一个复微分方程
$$\dot{z}=f(z,t)\tag{1}$$如果令$z=x+yi,f(z,t)=f(x+yi,t)=g(x,y,t)+i*h(x,y,t)$，则方程对应于
$$\begin{aligned}\dot{x}=g(x,y,t) \\ \dot{y}=h(x,y,t)\end{aligned}$$
这说明，二元微分方程在一定程度上等价于复微分方程。

点击阅读全文...

universe_mystery_expand

1929年哈勃(Edwin Hubble)对河外星系的视向速度与距离的关系进行了研究。当时只有46个河外星系的视向速度可以利用，而其中仅有24个有推算出的距离，哈勃得出了视向速度与距离之间大致的线性正比关系。

不少宇宙学的书籍中都提到了标题，那么，为什么哈勃定律是宇宙各向同性的体现？或者说为什么宇宙各向同性就必然导致哈勃定律？

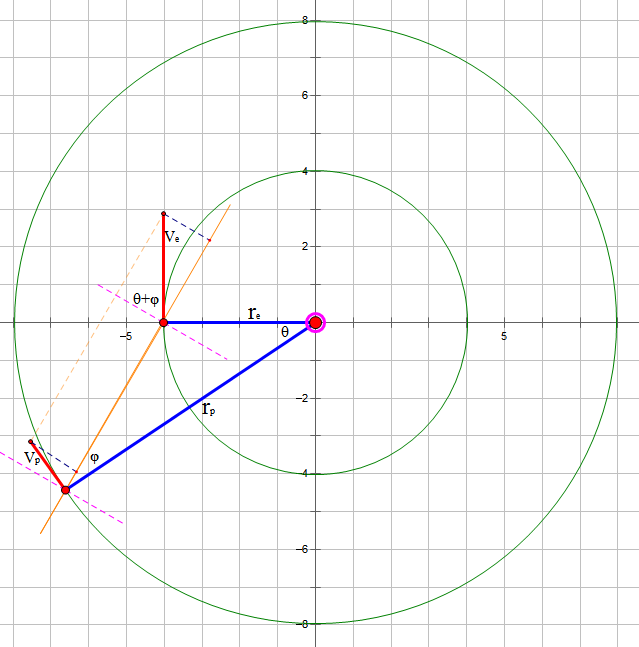
首先我们得需要了解一下宇宙学原理，它告诉我们宇宙在大尺度范围是均匀的、各向同性的。基于这个原理，我们会得到一些很奇怪的东西，如宇宙中的每一点都是宇宙的中心。另外，我们还可以得到：宇宙的（整体）运动情况在每一个方向都应该取相同的形式。

点击阅读全文...

$\sum_{i=0}^{\infty} a_i x^i=a_0+a_1 x+a_2 x^2+a_3 x^3+...$
最近为了数学竞赛，我研究了有关数列和排列组合的相关问题。由于我讨厌为某个问题而设计专门的技巧，所以我偏爱通用的方法，哪怕过程相对麻烦。因此，我对数学归纳法（递推法）和生成函数法情有独钟。前者只需要列出问题的递归关系，而不用具体分析，最终把问题转移到解函数方程上来。后者则巧妙地把数列${a_n}$与幂级数$\sum_{i=0}^{\infty} a_i x^i$一一对应，巧妙地通过代数运算或微积分运算等得到结果。这里我们不用考虑该级数的敛散性，只需要知道它对应着哪一个“母函数”（母函数展开泰勒级数后得到了级数$\sum_{i=0}^{\infty} a_i x^i$）。显然，这两种方法的最终，都是把问题归结为代数问题。

点击阅读全文...