《向量》系列——4.天旋地转(向量,复数,极坐标)

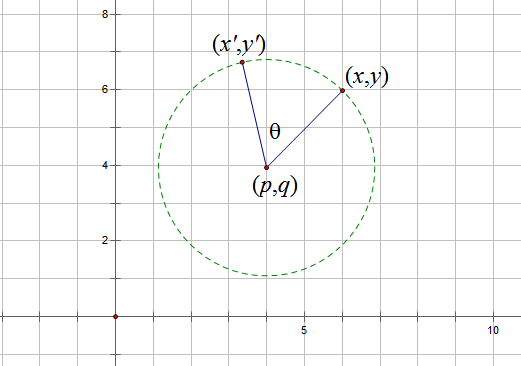
如图，坐标(x,y)绕点(p,q)逆时针旋转θ角后得到坐标(x',y')，求x',y'关于x,y的表达式。

之前我们已经讨论过这个问题，在《函数图像旋转公式》一文中，利用解析几何的方法进行了分析。那篇文章是在2月份完成的，那时还没有系统地学习向量和复数的相关知识，现在，BoJone从向量和复数两个角度，给出关于旋转公式的两个证明，仅供参考，如有错误，请指出。

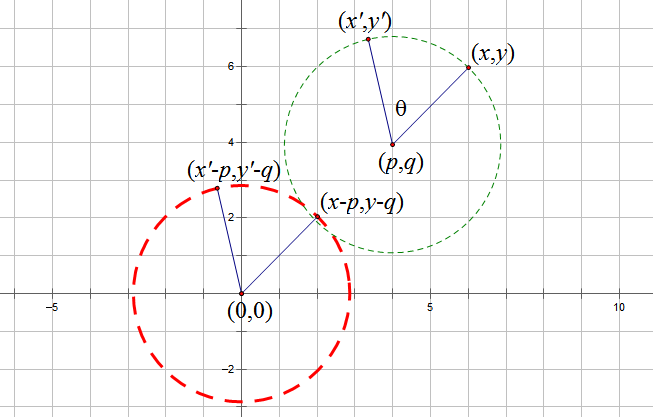
为了把问题化简，我们先做以下平移：

这样我们只需讨论旋转中心位于原点的问题。首先我们利用向量来求解。旋转前后的两个点分别用向量表示为$\vec{A}=(x-p,y-q,0),\vec{B}=(x'-p,y'-q,0),|\vec{A}|=|\vec{B}|=R$，那么有$\vec{A}\times\vec{B}=(0,0,(x-p)(y'-q)-(x'-p)(y-q))$，并且
$$\vec{A}\cdot \vec{B}=R^2 \cos\theta=(x-p)(x'-p)+(y-q)(y'-q)\tag{1}$$ $$|\vec{A}\times\vec{B}|=|R^2 \sin\theta|=|(x-p)(y'-q)-(x'-p)(y-q)|\tag{2}$$
考虑$0 < \theta <\pi$的情况：
$(1)\times (y-q)+(2)\times (x-p)$得到
$$\begin{aligned}(y'-q)[(y-q)^2+(x-p)^2]=R^2[(y-q)\cos\theta+(x-p)\sin\theta] \\ y'-q=(y-q)\cos\theta+(x-p)\sin\theta\end{aligned}\tag{3}$$ $(1)\times (x-p)+(2)\times (y-q)$得到
$$\begin{aligned}(x'-p)[(y-q)^2+(x-p)^2]=R^2[(x-p)\cos\theta-(y-q)\sin\theta] \\ x'-p=(x-p)\cos\theta-(y-q)\sin\theta\end{aligned}\tag{4}$$
(3)和(4)就是坐标旋转公式。在$\pi < \theta <2\pi$时形式一样。

接下来使用复数解答。我们知道，复数可以用复平面表示，并且两个复数相乘，结果也是复数，其模等于乘数模的积，辐角等于乘数辐角的和。于是我们不妨用$z_1=(x-p)+(y-q)i$来表示旋转前的点，用$z_2=(x'-p)+(y'-q)i$表示旋转后的点。很明显，z₂是由z₁乘上一个模等于1、辐角为θ的复数，不难得出，这个复数就是$cos\theta+i*sin\theta$。也就是说

$$\begin{aligned}[(x-p)+(y-q)i]\cdot [\cos\theta+(\sin\theta)i]=(x'-p)+(y'-q)i \\ [(x-p)\cos\theta-(y-q)\sin\theta]+[(y-q)\cos\theta+(x-p)\sin\theta]i \\ =(x'-p)+(y'-q)i\end{aligned}$$

根据复数相等的条件就有
$$\begin{aligned}y'-q=(y-q)\cos\theta+(x-p)\sin\theta \\ x'-p=(x-p)\cos\theta-(y-q)\sin\theta\end{aligned}$$

利用复数解答几何问题很重要的一点就是应用复数相等的条件是“实数部分=实数部分，虚数部分=虚数部分”。这样有时可以把问题回归到实数的范畴内，进而利用已知的知识解答。要想把复数更好地应用于几何，还要熟悉复平面的应用，关键是理解复数相关运算的几何意义。

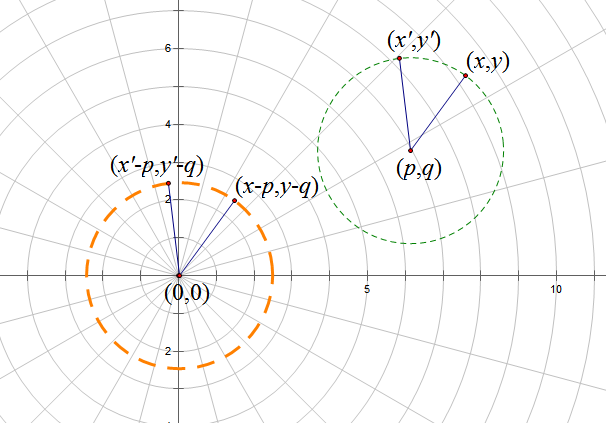
最后看一个利用极坐标的推导，由上图可以看出
$$x-p=r \cos f,y-q=r \sin f,r=\sqrt{(x-p)^2+(y-q)^2}$$
并且有
$$\begin{aligned}x'-p= r \cos (f+\theta)=r \cos f \cos\theta-r \sin f \sin\theta=(x-p)\cos\theta-(y-q)\sin\theta \\ y'-q= r \sin (f+\theta)=r \sin f \cos\theta + r \cos f \sin\theta=(y-q)\cos\theta+(x-p)\sin\theta\end{aligned}$$

证毕。

转载到请包括本文地址：https://spaces.ac.cn/archives/889

更详细的转载事宜请参考：《科学空间FAQ》