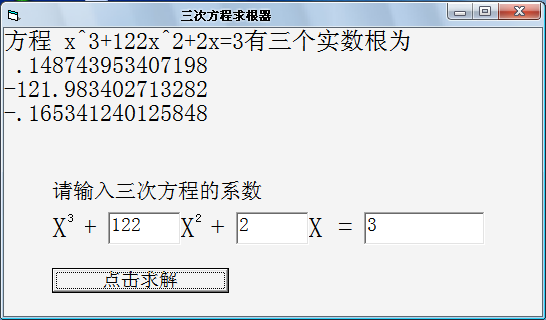
“n次方程有n个根”的证明
By 苏剑林 | 2010-02-27 | 70207位读者 | 引用(原创)切抛物线法解方程
By 苏剑林 | 2010-03-06 | 32555位读者 | 引用牛顿法使用的是函数切线的方程的零点来逼近原函数的零点,他所使用的是“切直线”,要是改为同曲率的“切抛物线”,则有更稳定的收敛效果以及更快的收敛速度
设函数$y=f(x)$在$(x_0,y_0)$处有一条“切抛物线”$y=ax^2+bx+c$,则应该有
$a(x_0+\Delta x)^2+b(x_0+\Delta x)+c=f(x_0+\Delta x)$-------(A)
$ax_0^2+bx_0+c=f(x_0)$-------(B)
$a(x_0-\Delta x)^2+b(x_0-\Delta x)+c=f(x_0-\Delta x)$-------(C)
其中$lim_{\Delta x->0}$
谈大气消光和大气折光
By 苏剑林 | 2010-03-06 | 38855位读者 | 引用苏剑林(BoJone) 编写/翻译
实际感受:
大家也许会有这样的生活经验:早上的太阳没有中午的太阳猛烈?从东方升起到我们的头顶,月亮一直在变“亮”?……这些现象都与地球大气的“消光”现象密切相关!
众所周知,地球有一层厚厚的大气,既是我们呼吸的来源,也是我们生命的保护伞。他为我们提供了臭氧层,也为我们提供了蓝天和风霜雨露,还为我们送上了绚丽的彩虹。然而,在天文学角度,大气却是我们的“障碍”,浓厚的大气不利于我们对宇宙进行清晰的观测。因此,天文学家们一直希望把天文台建立海拔更高的地方,因为那里有着稀薄的大气……为了渴求更高的清晰度,人们甚至把望远镜放到了地球之外。
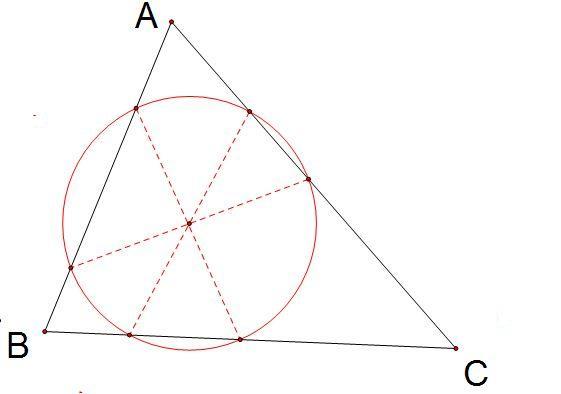
神秘的圆——三角形的“六接圆”(添加新方法)
By 苏剑林 | 2010-07-24 | 31529位读者 | 引用问世间质心(重心)知多少
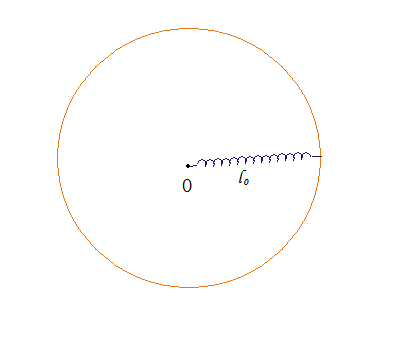
By 苏剑林 | 2010-07-26 | 44843位读者 | 引用从牛顿力学角度研究宇宙学
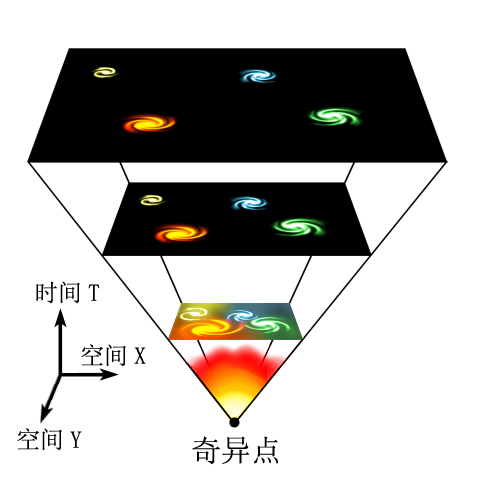
By 苏剑林 | 2010-06-17 | 47578位读者 | 引用不少天文爱好者对宇宙学这方面的内容“听而生畏”,觉得没有爱因斯坦的广义相对论等复杂理论基础是不可理解的。的确,这种观点没有错,当前的宇宙学对宇宙的精确描述,的确是建立在广义相对论和量子力学等理论的基础之上的。BoJone也只是在书上略略浏览,根本谈不上有什么了解。但是,对于一般的天文爱好者来说,只要对牛顿力学和微积分有一定的了解,就可以对我们的宇宙有一个大概的描述,也能够得出很多令人惊喜的结论。相信进行了这项工作之后,很多爱好者都会改观:原来宇宙学也并不是那么难...并且能够得出这样的一个结论:广义相对论虽然对牛顿引力理论进行了彻底的改革,但是从数学的角度来讲,它仅仅对牛顿力学进行了修正。










最近评论