[遐想]细胞的进化是一次次“大吞并”?
By 苏剑林 | 2011-11-06 | 41870位读者 | 引用传说中的高三备考是一次全面系统的大复习,但对于我们而言,它并不是复习,而是学习。我发现很多知识点在以前都是鲜有接触的,这无疑说明了两个问题:当时我学习得很肤浅;我的遗忘力太强了。就拿生物来说吧,以前总是很简单地就跳阅过去了,从不会去思考一些深入的问题。现在的重新“复习”阶段,却饶有兴趣地引出了很多的思考。特别是有关细胞进化的讨论,显得特别有趣。
根据古生物的研究,地球上第一个生命起源于32亿年前,是一个很简单的原核细胞,其遗传物质是RNA,后来逐渐演变成以DNA为遗传物质,例如细菌有一个环状的DNA分子。原核生物很快就进化出了真核生物,因为迄今所知最古老的真核生物化石已有近21亿年的历史,许多科学家推测,最早的真核生物可能早在30亿年前就出现了。
这里便引申出了一个问题:病毒是什么时候出现的?它是怎么出现的?
不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 42173位读者 | 引用《方程与宇宙》:三体问题和它的初积分(六)
By 苏剑林 | 2011-01-20 | 61995位读者 | 引用The Three Body Problem and its Classical Integration
很多天文爱好者都已经接触到了“二体问题”(我们在高中学习到的“开普勒三定律”就是内容之一),由于在太阳系中行星质量相对较小而且距离相对较远,应用“二体问题”的解对天体进行计算、预报等能够满足一定的近似需求。不过,如果需要更高精度的计算,就不能把其他行星的引力给忽略掉了,于是就产生了所谓N体问题(N-Body Problem),即N个质点尽在它们各自引力的相互作用下的运动规律问题。最简单的二体已经被彻底解决,而三体或更多体的问题则与二体大相径庭,因为庞加莱证明了,三体问题不能严格求解,而且这是一个混沌系统,任何微小的扰动都会造成不可预期的效果。
根据牛顿力学,选择惯性参考系,设三个质点分别为$M_1,M_2,M_3$,向径分别为$\vec{r_1},\vec{r_2},\vec{r_3}$,可以列出运动方程(以下的导数都默认是对时间t求导)
[春礼]《方程与宇宙》:圆形限制性三体问题(七)
By 苏剑林 | 2011-02-04 | 23766位读者 | 引用平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正!!
寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破,于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”,遗憾的是,“有心栽花花不开”,到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”,也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”,经过一番思考,利用这些天的思考方法重新推导出了其运动方程和能量积分,也算是“意外收获”在此作为春节礼物与大家分享。
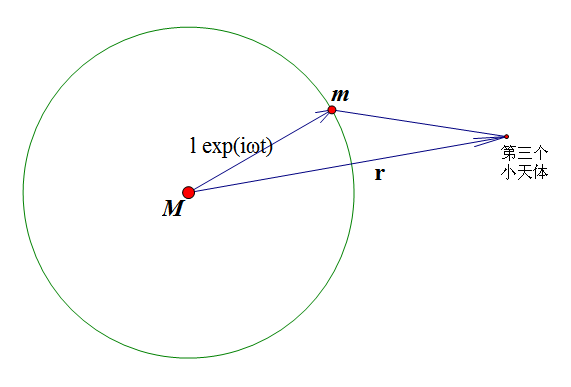
所谓“圆形限制性三体问题”,就是指两个大质量天体(质点)在它们相互引力作用下做圆周运动,假设第三天体(质量趋于0)只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分,而这个“限制性模型”能够把问题化简不少(不过还是不能积分出来的),因此也得到了一定应用。它的应用条件是:第三体质量小(如当前航天器与地球、太阳)、短程。注意短程也是相当重要的条件之一,注意短程也是相当重要的条件之一,质量越小应用范围越大。要是质量大的话,就不能计算太长的路程。
《方程与宇宙》:限制性三体的那些事儿(八)
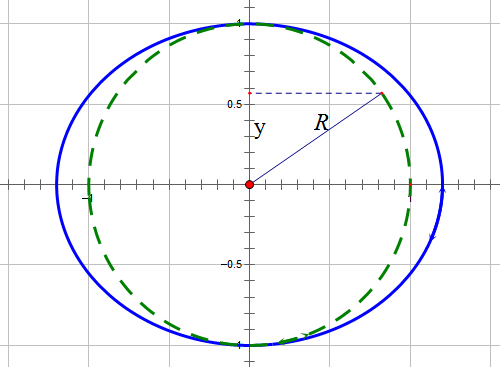
By 苏剑林 | 2011-02-04 | 26759位读者 | 引用在上一些关于限制性三体问题的探讨中,我们得出了在平面上的方程:
$$\ddot{R}+2i\omega \dot{R}=\omega^2 R-GM\frac{R-l_1}{|R-l_1|^3}-Gm\frac{R-l_2}{|R-l_2|^3}\tag{32}$$
能量积分为:
$$\frac{1}{2}|\dot{R}|^2=\frac{1}{2} \omega^2 |R|^2+\frac{GM}{|R-l_1|}+\frac{Gm}{|R-l_2|}-C\tag{33}$$
下面就以这两个方程为基础,再说说限制性三体问题的那些事儿...
施密特系统的校正镜方程求解
By 苏剑林 | 2011-02-11 | 31851位读者 | 引用非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope
本文在牧夫天文论坛的讨论:
http://www.astronomy.ac/bbs/thread-160257-1-1.html
为了克服折射望远镜的色差问题,1670年,牛顿制造了第一台实用的反射式望远镜,将望远镜的主镜由玻璃透镜换成了抛物反射面,从而消除了色差。然而,相比球面镜,大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了,而抛物线每点的曲率并不相等,所以需要逐个磨制曲率不等的小镜片,并按照严格的顺序组合起来。这无疑大大增加了磨制难度。
为了解决这一难题,天文学家们想到了一个折衷的办法:以球面为主镜,并配以校正镜来校正球差。迎着这一思路,施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而,校正镜是一个比抛物面更加复杂的四次曲面,磨制工艺要求更高,因此,校正镜也不宜过大。
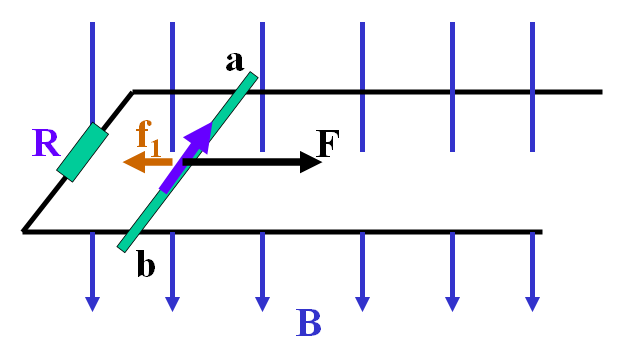
线圈感抗和电容容抗的计算
By 苏剑林 | 2011-02-26 | 52679位读者 | 引用学到人教版高二物理选修3-2的同学们,眼前会出现许多新的名词,如楞次定律、自感(电感)、感抗、容抗等等。其中对于电感,在中文维基百科给予的解释为:当电流改变时,因电磁感应而产生抵抗电流改变的电动势(EMF,electromotive force)。电路中的任何电流,会产生磁场,磁场的磁通量又作用于电路上。依据楞次定律,此磁通会借由感应出的电压(反电动势)而倾向于抵抗电流的改变。磁通改变量对电流改变量的比值称为自感,自感通常也就直接称作是这个电路的电感。
自感的计算公式为:$U=-L\frac{dI}{dt}$,U是自感电动势,I是电流,负号表示自感电动势反抗原来的电流。L是比例系数,就称为电感,对于同一个线圈来说,L是常数,单位是$V\cdot t//A=\Omega \cdot t$,同时也简记为$H$(亨利)。











最近评论