文章转载于：http://gerry.lamost.org/blog/?p=417
logo_iya2009
去年是国际天文年，在翻译官方宣传手册之外，还在朋友们的鼓励下给《天文爱好者》写了一年的连载，介绍著名星表。编辑李鉴给这个系列起了个很棒的名字：“群星的族谱”。前后四五百年，二十多代天文学家，上千个星表，在新线索的串联下，发展脉络清晰可见。我常常因为灵光乍现激动得匆匆提笔，却在下笔的一刻冒出更多的问题……在积累有限之外，自己的笔力也还不足以驾驭这样宏大的题材，就当成框架索引来看好了。虽然遗憾种种，但总算是完成了
一个心愿。这里是这个系列的番外篇，介绍星表数据库，发表在2010年1月的爱好者杂志上。
讲星表，就不能不提到法国斯特拉斯堡天文数据中心（Strasbourg Astronomical Data Center），这个始建于1972年的数据中心汇集了有文献记载的近万个星表，提供了详尽的查询方式，是天文学家获取数据的首选。而它的身世却少有人知……
1
Feb
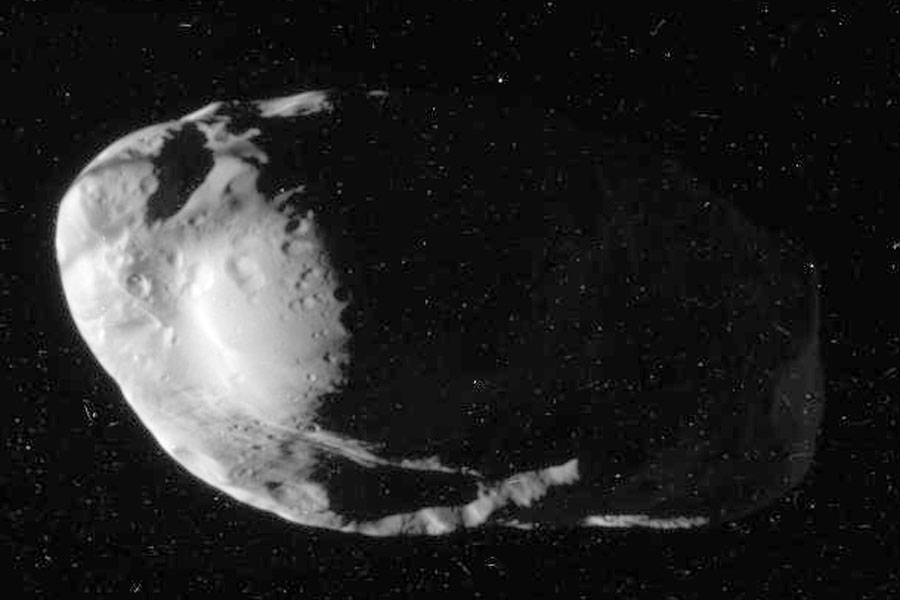
【NASA每日一图】牧羊卫星Prometheus
By 苏剑林 | 2010-02-01 | 34022位读者 | 引用
26
Jul
问世间质心(重心)知多少
By 苏剑林 | 2010-07-26 | 45927位读者 | 引用
19
Jul
太阳中心的压强和温度
By 苏剑林 | 2010-07-19 | 32199位读者 | 引用
太阳
为了准备IOAA，同时也加深对天体物理的理解，所以就系统地学习一下天体物理学了。今天看到“太阳”这一章，并由此简单估算了一下太阳的中心压强和温度。
天体物理学给出了关于恒星结构的一些方程。假设存在一颗各项同性的球形恒星，则有
$\frac{dm(r)}{dr}=4\pi r^2 \rho(r)$————质量方程
其中m(r)是与恒星球心距离为r的一个球形区域内的总质量，$\rho(r)$是距离球心r处的物质的密度。我们也可以写成积分的形式
$$m(r)=\int_0^R 4\pi r^2 \rho(r)dr$$
其中R是恒星半径。这个方程的意思其实就是每一个壳层的质量叠加，所以就不详细推导了。
29
Jul
R136a1,300倍太阳质量的怪兽星
By 苏剑林 | 2010-07-29 | 28088位读者 | 引用原文链接：http://www.eso.org/public/news/eso1030/
译文来自：http://www.astronomy.com.cn/bbs/thread-141201-1-1.html
Stars Just Got Bigger 超大质量的巨星 A 300 Solar Mass Star Uncovered 发现超过300太阳质量的蓝超巨星
Using a combination of instruments on ESO’s Very Large Telescope, astronomers have discovered the most massive stars to date, one weighing at birth more than 300 times the mass of the Sun, or twice as much as the currently accepted limit of 150 solar masses. The existence of these monsters — millions of times more luminous than the Sun, losing weight through very powerful winds — may provide an answer to the question “how massive can stars be?”
借助于ESO的甚大望远镜（VLT），天文学家发现了创质量纪录的巨星——达300个太阳质量以上，是我们此前公认的（星族II）恒星质量上限——150个太阳的2倍。发现如此怪兽级恒星：光度是太阳的数百万倍，以极速恒星风迅速损失质量——由此产生了一个问题：恒星质量上限到底是多少？
23
Aug
《向量》系列——4.天旋地转(向量,复数,极坐标)
By 苏剑林 | 2010-08-23 | 40085位读者 | 引用
6
Nov
警察捉贼,追牛问题,导弹跟踪
By 苏剑林 | 2010-11-06 | 53862位读者 | 引用王二小的牛跑了，当他发现时，牛在他正南方300米。且一直向正西方向匀速的跑，王二小立即追牛，他不是朝着一个固定的方向，而是每时每刻都朝着牛的方向跑，且速度是牛速度的4/3倍。当他追上牛时王二小共跑了多远？
问题分析
米拉斯反潜导弹
咋看起来，追牛和导弹是风牛马不相及的两件事：一个是生活小事，一个是物理问题，怎么能够扯到一块呢？
回想一下平时警察抓小偷的过程。警察不是物理学家，不会也可不能先去研究小偷的逃走路线函数，然后设计最小追赶时间的路程吧？那么，在不能预知小偷逃跑路线的前提下，警察要怎样捉小偷呢？很简单，盯死他！是的，只要你以更快的速度，一直朝着他跑，总能够追到的。继续联想下：要想用导弹跟踪摧毁一首敌舰，不也是只能够采用这种方式吗？回看文章开始的“追牛问题”，本质上不是一样的吗？以下是上海交大提出的导弹跟踪问题：
7
Nov
最近评论