警察捉贼,追牛问题,导弹跟踪
By 苏剑林 | 2010-11-06 | 71330位读者 |王二小的牛跑了,当他发现时,牛在他正南方300米。且一直向正西方向匀速的跑,王二小立即追牛,他不是朝着一个固定的方向,而是每时每刻都朝着牛的方向跑,且速度是牛速度的4/3倍。当他追上牛时王二小共跑了多远?
问题分析 #
咋看起来,追牛和导弹是风牛马不相及的两件事:一个是生活小事,一个是物理问题,怎么能够扯到一块呢?
回想一下平时警察抓小偷的过程。警察不是物理学家,不会也可不能先去研究小偷的逃走路线函数,然后设计最小追赶时间的路程吧?那么,在不能预知小偷逃跑路线的前提下,警察要怎样捉小偷呢?很简单,盯死他!是的,只要你以更快的速度,一直朝着他跑,总能够追到的。继续联想下:要想用导弹跟踪摧毁一首敌舰,不也是只能够采用这种方式吗?回看文章开始的“追牛问题”,本质上不是一样的吗?以下是上海交大提出的导弹跟踪问题:
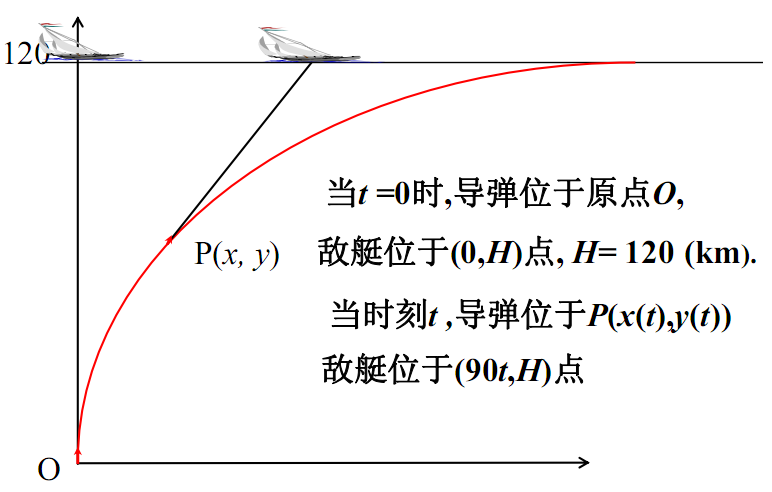
某军的一导弹基地发现正北方向120 km处海面上有敌艇一艘以90 km/h的速度向正东方向行驶. 该基地立即发射导弹跟踪追击敌艇,导弹速度为450 km/h,自动导航系统使导弹在任一时刻都能对准敌艇。试问导弹在何时何处击中敌艇?
建立坐标系:
设导弹速度为$u$,敌艇速度为$v$,可以列出
$$dx^2+dy^2=u^2 dt^2\tag{1}$$
$$\frac{dy}{dx}=\frac{H-y}{vt-x}\tag{2}$$
欲擒故纵 #
解微分方程组的一般思想是:消元、降阶。要是对微分方程不熟悉,或者是刚入门的朋友,也许马上会想到的步骤是降阶,而忽略了先消元,导致无从下手。因为在我们的头脑中的潜意识告诉我们,高阶方程总比低阶麻烦,化低阶为高阶是自找麻烦。其实不然,为了消元,我们需要“欲擒故纵”,即“升阶”!
我们设法消去$t$,将$(2)$变换成$\frac{dx}{dy}(H-y)=vt-x$,两边微分即得
$$d\left(\frac{dx}{dy}\right)(H-y)-\frac{dx}{dy}\cdot dy=v dt-dx\tag{3}$$
此式等价于$\frac{d\left(\frac{dx}{dy}\right)}{dy} \frac{dy}{dt}(H-y)=v$,由$(1)$式可以得到
$$\frac{dy}{dt}=\frac{u}{\sqrt{\left(\frac{dx}{dy}\right)^2+1}}$$
代入上式,得到
$$\frac{d\left(\frac{dx}{dy}\right)}{dy} \frac{u}{\sqrt{\left(\frac{dx}{dy}\right)^2+1}}(H-y)=v$$
直捣黄龙 #
消元完毕后,我们需要就是降阶、分离变量等,把最终结果就出来。在消元时还可以比较一下究竟消去哪个未知数后会使微分方程的形式相对简单一点。例如在上述问题中,我们得到了一个可以分离变量的方程,这胜了我们不少功夫。如果选择消去y,则不能出现可以分离变量的方程,那会令我们的计算更复杂。
令$\frac{v}{u}=k$,即得
$$\frac{d\left(\frac{dx}{dy}\right)}{\sqrt{\left(\frac{dx}{dy}\right)^2+1}}=\frac{k dy}{H-y}$$
两端积分得
$$\ln\left(\frac{dx}{dy}+\sqrt{\left(\frac{dx}{dy}\right)^2+1}\right)=-k \ln(H-y)+C$$
代入初始条件$\frac{dx}{dy}=0,y=0$,即有$C=k \ln H$。各项取幂,得到
$$\begin{aligned}&\frac{dx}{dy}+\sqrt{\left(\frac{dx}{dy}\right)^2+1}=(\frac{H}{H-y})^k \\ &\frac{dx}{dy}=\frac{1}{2}\left[\left(\frac{H}{H-y}\right)^k-\left(\frac{H}{H-y}\right)^{-k}\right] \\ &2dx=[(1-y/H)^{-k}-(1-y/H)^k]dy\end{aligned}$$
两端积分,并代入初始量$x=0,y=0$,即得
$$x=\frac{1}{2} \left[-\frac{1}{-k+1}(1-y/H)^{-k+1}+\frac{1}{k+1}(1-y/H)^{k+1}\right]+\frac{kH}{1-k^2}$$
至此,问题解决。摧毁它所需要的时间为$T=\frac{Hu}{u^2-v^2}$
但是,有朋友会问,要是敌舰速度和导弹速度均不是常数,而是$t$的函数,那该怎么解这一类方程呢?这时我们可以选择消去$x$,首先约定$\dot{x}$表示是对自变量$t$的导数$\frac{dx}{dt}$,也是从$(3)$式出发,把$\frac{dx}{dy}$改成$\frac{\dot{x}}{\dot{y}}$,从$(1)$式解出$\dot{x}=\sqrt{u^2-\dot{y}^2}$,代入、消元,有兴趣的朋友可以自己推算,这里贴出BoJone的计算结果:
$$\frac{u\dot{u}\dot{y}-u^2 \ddot{y}}{\dot{y}^2 \sqrt{u^2-\dot{y}^2}}=\frac{\dot{s}}{H-y}$$
这里的$s\equiv s(t)$是被最终者的路程函数,上式是关于$y$和$t$的二阶微分方程。
(感谢上海交通大学数学系,这里提供上海交大的课件下载:导弹追踪(07.3).rar)
转载到请包括本文地址:https://spaces.ac.cn/archives/1047
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Nov. 06, 2010). 《警察捉贼,追牛问题,导弹跟踪 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1047
@online{kexuefm-1047,
title={警察捉贼,追牛问题,导弹跟踪},
author={苏剑林},
year={2010},
month={Nov},
url={\url{https://spaces.ac.cn/archives/1047}},
}











November 8th, 2010
三棱锥中四个面能不能全为钝角三角形
怎么证明,,,如果不用余弦定理????????
November 8th, 2010
我暂时先看了问题,查了《趣味数学百科图典》。它说,这种曲线被称作“追逐曲线”,是条等角螺线。还有一种曲线叫“拽物线”,一个小孩用细绳斜拖一玩具车,玩具车所行路线就是“拽物线”,与“追逐曲线”是同一种。把“拽物线”绕它的渐近直线旋转一周,就形成了一个喇叭状的曲面,叫做“伪球面”,罗氏非欧几何在该曲面上成立。
你能否算出曳物线的参数方程
恐怕我还没达到那个境界。
不过网络上有关于曳物线的资料(前面把“曳”打成“拽”属笔误,在此修正)。
不会的,你要相信自己。那个方程是很容易的。我说的是实话,几步就搞定了
同意zzm.
感谢大家鼓励。我的想法:物体$A$由原点出发,沿正$x$轴方向拖拽起初位于正$y$轴的物体$B$,绳长为$a$,推导曲线方程。冥思苦想了半天,导出了这样一个式子:$\int dx=-\int \frac{\sqrt{a^2-y^2}}{y}dy$,且$x(a)=0$。
恭喜你,这是对的。
May 19th, 2024
根据定义令$x' = dx/dy$ ,它的方向为
$x'= (vt - x)/(H - y)$
进一步有 $vt = x + (H - y)x'$
同时假设舰船与导弹的速度之比为$k$ 则在$t$ 时刻有
$\int_{0}^y \sqrt{1 + x'^2} dy = (v/k)t=x/k + (H - y)x'/k$
左边为以弧长表示导弹行驶的距离,右边表示速度和时间表示的距离
两边同时对$y$ 求导,则有
$\sqrt{1 + x'^2} = x'/k + (1/k)[-1 x' + x''(H - y)]=(1/k)(H - y)x''$
$\frac{x''}{\sqrt{1 + x'^2}} = \frac{k}{(H - y)}$
两边同时对$y$ 积分有(查积分表)
$\ln (x' + \sqrt{x' + 1}) = -k \ln(H - y) + C$