科学空间|Scientific Spaces

向量与联络

当我们在我们的位置建立起自己的坐标系后，我们就可以做很多测量，测量的结果可能是一个标量，比如温度、质量，这些量不管你用什么坐标系，它都是一样的。当然，有时候我们会测量向量，比如速度、加速度、力等，这些量都是客观实体，但因为测量结果是用坐标的分量表示的，所以如果换一个坐标，它的分量就完全不一样了。

假如所有的位置都使用同样的坐标，那自然就没有什么争议了，然而我们前面已经反复强调，不同位置的人可能出于各种原因，使用了不同的坐标系，因此，当我们写出一个向量$A^{\mu}$时，严格来讲应该还要注明是在$\boldsymbol{x}$位置测量的：$A^{\mu}(\boldsymbol{x})$，只有不引起歧义的情况下，我们才能省略它。

到这里，我们已经能够进行一些计算，比如$A^{\mu}$是在$\boldsymbol{x}$处测量的，而$\boldsymbol{x}$处的模长计算公式为$ds^2 = g_{\mu\nu} dx^{\mu} dx^{\nu}$，因此，$A^{\mu}$的模长为$\sqrt{g_{\mu\nu} A^{\mu}A^{\nu}}$，它是一个客观实体。

如图，可以在球面上每一点建立不同的局部坐标系，至少这些坐标系的竖直方向的轴指向是不一样的。

点击阅读全文...

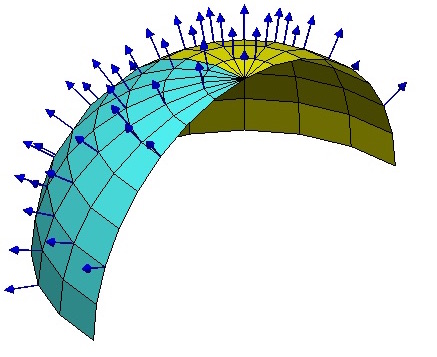
现在我们来关注黎曼曲率。总的来说，黎曼曲率提供了一种方案，让身处空间内部的人也能计算自身所处空间的弯曲程度。俗话说，“不识庐山真面目，只缘身在此山中”，还有“当局者迷，旁观者清”，等等，因此，能够身处空间之中而发现空间中的弯曲与否，是一件很了不起的事情，就好像我们已经超越了我们现有的空间，到了更高维的空间去“居高临下”那样。真可谓“心有多远，路就有多远，世界就有多远”。

如果站在更高维空间的角度看，就容易发现空间的弯曲。比如弯曲空间中有一条测地线，从更高维的空间看，它就是一条曲线，可以计算曲率等，但是在原来的空间看，它就是直的，测地线就是直线概念的一般化，因此不可能通过这种途径发现空间的弯曲性，必须有一些迂回的途径。可能一下子不容易想到，但是各种途径都殊途同归后，就感觉它是显然的了。

怎么更好地导出黎曼曲率来，使得它能够明显地反映出弯曲空间跟平直空间的本质区别呢？为此笔者思考了很长时间，看了不少参考书（《引力与时空》、《场论》、《引力论》等），比较了几种导出黎曼曲率的方式，简要叙述如下。

点击阅读全文...

曲率的独立分量

黎曼曲率张量是一个非常重要的张量，当且仅当它全部分量为0时，空间才是平直的。它也出现在爱因斯坦的场方程中。总而言之，只要涉及到黎曼几何，黎曼曲率张量就必然是核心内容。

已经看到，黎曼曲率张量有4个指标，这也意味着它有$n^4$个分量，$n$是空间的维数。那么在2、3、4维空间中，它就有16、81、256个分量了，可见，要计算它，是一件相当痛苦的事情。幸好，这个张量有很多的对称性质，使得独立分量的数目大大减少，我们来分析这一点。

首先我们来导出黎曼曲率张量的一些对称性质，这部分内容是跟经典教科书是一致的。定义
$$R_{\mu\alpha\beta\gamma}=g_{\mu\nu}R^{\nu}_{\alpha\beta\gamma} \tag{50} $$
定义这个量的原因，要谈及逆变张量和协变张量的区别，我们这里主要关心几何观，因此略过对张量的详细分析。这个量被称为完全协变的黎曼曲率张量，有时候也直接叫做黎曼曲率张量，只要不至于混淆，一般不做区分。通过略微冗长的代数运算（在一般的微分几何、黎曼几何或者广义相对论教材中都有），可以得到
$$\begin{aligned}&R_{\mu\alpha\beta\gamma}=-R_{\mu\alpha\gamma\beta}\\
&R_{\mu\alpha\beta\gamma}=-R_{\alpha\mu\beta\gamma}\\
&R_{\mu\alpha\beta\gamma}=R_{\beta\gamma\mu\alpha}\\
&R_{\mu\alpha\beta\gamma}+R_{\mu\beta\gamma\alpha}+R_{\mu\gamma\alpha\beta}=0
\end{aligned} \tag{51} $$

点击阅读全文...

科学空间是使用typecho程序搭建的博客，侧边栏提供了搜索功能，然而typecho内置搜索功能仅仅是基于字符串的全匹配查找，因此导致很多合理的查询都没法得到结果，比如“2018天象”、“新词算法”都没法给出结果，原因就是文章中都不包含这些字符串。

于是就萌生了加强搜索功能的想法，之前也有读者建议过这个事情。这两天搜索了一下，本来计划用Python下的Whoosh库来建立一个全文检索引擎，但感觉整合和后期维护的工作量太大，还是放弃了。后来想到在typecho自身的搜索上加强，在公司同事（大佬）的帮助下，完成了这个改进。

由于是直接修改typecho源文件实现的改进，因此如果typecho升级后就可能被覆盖，因此在这里做个备忘。

探索

通过在Github检索我发现，typecho的搜索功能是在var/Widget/Archive.php中实现的，具体代码大概在1185～1192行：

点击阅读全文...

首先感谢Shea和叶泉志的努力，文章中引用了他们俩的内容。还有“科学松鼠会”、“中国彗星与流星资讯网”、“牧夫天文论坛”等网站。

注意！！地球正在进入斯威夫特-塔特尔彗星所留下的尘埃带中，这里正是一年一度英仙座流星雨的发源地。虽然英仙座流星雨要到8月11-12日才会达到顶峰，但是好戏已经开始上演了。

之前在8月天象预报中已经介绍过8月的这一场盛大流星雨了。现在我们针对性地来看下！英仙座流星雨被称为“三大”之一。今年英仙座流星雨的传统峰值预计落在8月13日1:30-4:00（北京时间）。全球最佳观测位置是美国的芝加哥和华盛顿等地区。

点击阅读全文...

内容来源于：http://www.verycd.com/topics/2777592/

站长注：虽然有电子版，但是还是建议没有购买纸版的读者到书店或者网上购买一本。一是为了支持科学松鼠会和中国科学出版事业，二是拿着一本纸版书细细品味的感觉是读电子书绝对感受不到的。

《当彩色的声音尝起来是甜的》

《当彩色的声音尝起来是甜的》是科学松鼠会出版的第一本书，站长在得到消息后的第一时间，就在卓越上购买了它。这本书由上海三联书店出版。本书不是一本博客集，出自松鼠会网站的文章只占了1/3。全书54篇文章，精选自百位松鼠近三年创作的上千篇文章，从口腔溃疡到国际空间站，从玫瑰花到数学思想实验，内容天马行空，文字灵动活泼，一改传统科普的严肃面孔。

点击阅读全文...

3月份，大地回暖，春暖花开了，精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星，火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节，许多有趣、朦胧的深空天体，无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书，新手不妨作为入门的参考书。

梅西叶马拉松是一个自我挑战性相对较强的活动，因为虽然一夜之间所有的梅西耶天体全都亮相，但是因为升起的时间相差很多，有些天体的角度就很低了，并不十分适宜观测，况且一夜之间观测103个天体，即使对星空和器材性能非常熟悉，也需要相当时间（当然啦，你如果有电动赤道仪和导星输入的话，就很简单拉），这会是一个非常辛苦的活动，需要充分准备。 爱好挑战困难者，上吧，探索我们的宇宙！

点击阅读全文...

本文其实好几个月前就已经写好了，讲的是我最感兴趣的天体力学领域的故事，已经发表在2012年11月的《天文爱好者》上。

天体力学巨匠——拉普拉斯

作为一本天文科普杂志，《天文爱好者》着眼于普及天文，内容偏向于有趣的天体物理等，比较少涉及到天体力学。事实上，在天文发展史中，天体力学——研究天体纯粹在万有引力作用下演化的科学——占据了相当重要的地位。过去，天文就被划分为天体力学、天体物理以及天体测量学三个大块。只是在近现代，由于电子计算机的飞速发展，天体力学的多数问题都交给了计算机数值计算解决，因此这一领域逐渐淡出了人们视野。不过，回味当初那段天体力学史，依然让我们觉得激动人心。

首先引入“天体力学（Celestial mechanics）”这一术语的是法国著名数学家、天文巨匠拉普拉斯。他的全名为皮埃尔?西蒙?拉普拉斯（Pierre?Simon marquis de Laplace），因研究太阳系稳定性的动力学问题被誉为法国的牛顿和天体力学之父。他和生活在同一时代的法国著名数学家拉格朗日以及勒让德（Adrien-Marie Legendre）并称为“三L”。

神秘的少年时期

由于1925年的一场大火，很多拉普拉斯的生活细节资料都丢失了。根据W. W. Rouse Ball的说法，他可能是一个普通农民或农场工人的儿子，1749年3月23日出生于诺曼底卡尔瓦多斯省的伯蒙特恩奥格。少年时期，拉普拉斯凭借着自己的才能和热情，在富人邻居的帮助下完成了学业。他父亲希望这能使他将来以宗教为业，16岁时，他被送往卡昂大学读神学。但他很快在数学上显露头角。

点击阅读全文...