科学空间|Scientific Spaces

《量子力学与路径积分》封面

今天收到高教出版社的王超编辑寄来的费曼著作新版《量子力学与路径积分》了，兴奋ing...

《量子力学与路径积分》是费曼的一本经典著作，更是量子力学的经典著作——它是我目前读过的唯一一本从路径积分出发、并且以路径积分为第一性原理的量子力学著作(徐一鸿的《简明量子场论》好象是我读过的唯一一本纯粹以路径积分为方法的量子场论著作，也非常不错)，其它类型的量子力学著作，也有部分谈到路径积分，但无一不是从哈密顿形式中引出路径积分的，在那种情况之下，路径积分只能算是一个推论。但是路径积分明明就作为量子力学的三种形式之一，它应该是可以作为量子力学的基本原理来提出的，而不应该作为另一种形式的推论。费曼做了尝试——从路径积分出发讲解量子力学，而且显然这种尝试是很成功的，至少对于我来说，路径积分是一种非常容易理解的量子力学形式。（这也许跟我的数学基础有关）

点击阅读全文...

本文以尽可能清晰、简明的方式来介绍了一阶偏微分方程的特征线法。个人认为这是偏微分方程理论中较为简单但事实上又容易让人含糊的一部分内容，因此尝试以自己的文字来做一番介绍。当然，更准确来说其实是笔者自己的备忘。

拟线性情形

一般步骤

考虑偏微分方程
$$\begin{equation}\boldsymbol{\alpha}(\boldsymbol{x},u) \cdot \frac{\partial}{\partial \boldsymbol{x}} u = \beta(\boldsymbol{x},u)\end{equation}$$
其中$\boldsymbol{\alpha}$是一个$n$维向量函数，$\beta$是一个标量函数，$\cdot$是向量的点积，$u\equiv u(\boldsymbol{x})$是$n$元函数，$\boldsymbol{x}$是它的自变量。

点击阅读全文...

笔者成功地保研到了中山大学的基础数学专业，这个专业自然是比较理论性的，虽然如此，我还会保持着我对数据分析、计算机等方面的兴趣。这几天兴致来了，想做一下结合我的专业跟数据挖掘相结合的研究，所以就爬取了ARXIV上面近五年（2010年到2014年）的数学论文（包含的数据有：标题、分类、年份、月份），想对这几年来数学的“行情”做一下简单的分析。个人认为，ARVIX作为目前全球最大的论文预印本的电子数据库，对它的数据进行分析，所得到的结论是能够具有一定的代表性的。

当然，本文只是用来练手爬虫和基本数据分析的文章，并没有挖掘出特别有价值的信息。文末附录了笔者爬取到的数据，供有兴趣的读者进一步分析研究。

整体情况

这五年来，ARXIV的数学论文总数为135009篇，平均每年27000篇，或者每天74篇。

点击阅读全文...

最近一直在考虑一些自然语言处理问题和一些非线性分析问题，无暇总结发文，在此表示抱歉。本文要说的是对于一阶非线性差分方程（当然高阶也可以类似地做）的一种摄动格式，理论上来说，本方法可以得到任意一阶非线性差分方程的显式渐近解。

非线性差分方程

对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说，差分方程很少有解析解，因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候，我们首先会考虑将差分替换为求导，得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因，除了微分方程有比较简单的显式解之外，另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质，如渐近性。例如，考虑离散的阻滞增长模型：
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为（差分替换为求导）：
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
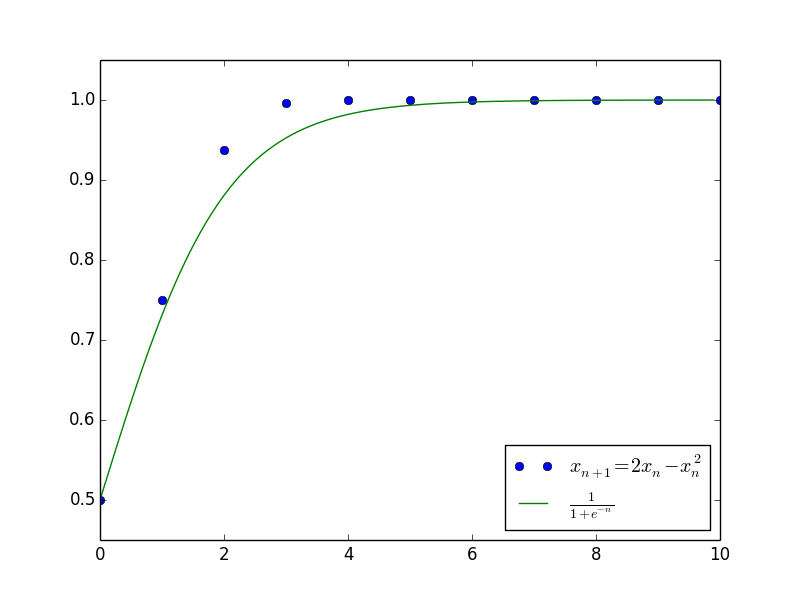
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势，并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$（即$x_0=\frac{1}{2}$）时，微分方程的解与差分方程的解的值比较。

差分方程的摄动法1

现在的问题是，既然微分方程的解可以作为一个形态良好的近似解了，那么是否可以在微分方程的解的基础上，进一步加入修正项提高精度？

点击阅读全文...

流年

《量子力学与路径积分》的习题解答终于艰难地推进到了0.4版本，目前已经基本完成了前7章的习题。

今天已经是2016年1月9号了，2015年已经远去，都忘记跟大家说一声新年快乐了，实在抱歉。在这里补充一句：祝大家新年快乐，事事如意！。

笔者已经大四了，现在是临近期末考，又临近毕业。最近忙的事情有很多，其中之一是我加入了一个互联网小公司的创业队伍中，负责文本挖掘，偶尔也写写爬虫，等等，感觉自己进去之后，增长了不少见识，也增加了不少技术知识，较之我上一次实习，又有不一样的高度。现在里边有好几样事情排队着做，可谓忙得不亦悦乎了。还有，我也开始写毕业论文了，早点写完能够多点时间，学学自己喜欢的东西，毕业论文我写的是路径积分相关的内容，自我感觉写得还是比较清楚易懂的，等时机成熟了，发出来，向大家普及路径积分^_^。此外，每天做点路径积分的习题，也要消耗不少时间，有些比较难的题目，基本一道就做几个早上才能写出比较满意的答案。总感觉想学的想做的事情有很多，可是时间很少。

点击阅读全文...

问题来源

笔者经常学习的数学研发论坛曾有一帖讨论下述非线性差分方程的渐近求解：
$$a_{n+1}=a_n+\frac{1}{a_n^2},\, a_1=1$$
原帖子在这里，从这帖子中我获益良多，学习到了很多新技巧。主要思路是通过将两边立方，然后设$x_n=a_n^3$，变为等价的递推问题：
$$x_{n+1}=x_n+3+\frac{3}{x_n}+\frac{1}{x_n^2},\,x_1=1$$
然后可以通过巧妙的技巧得到渐近展开式：
$$x_n = 3n+\ln n+a+\frac{\frac{1}{3}(\ln n+a)-\frac{5}{18}}{n}+\dots$$
具体过程就不提了，读者可以自行到上述帖子学习。

然而，这种形式的解虽然精妙，但存在一些笔者不是很满意的地方：

1、解是渐近的级数，这就意味着实际上收敛半径为0；
2、是$n^{-k}$形式的解，对于较小的$n$难以计算，这都使得高精度计算变得比较困难；
3、当然，题目本来的目的是渐近计算，但是渐近分析似乎又没有必要展开那么多项；
4、里边带有了一个本来就比较难计算的极限值$a$；
5、求解过程似乎稍欠直观。

当然，上面这些缺点，有些是鸡蛋里挑骨头的。不过，也正是这些缺点，促使我寻找更好的形式的解，最终导致了这篇文章。

点击阅读全文...

在这篇文章中，我们暂停查词典方法的介绍，转而介绍字标注的方法。前面已经提到过，字标注是通过给句子中每个字打上标签的思路来进行分词，比如之前提到过的，通过4标签来进行标注（single，单字成词；begin，多字词的开头；middle，三字以上词语的中间部分；end，多字词的结尾。均只取第一个字母。），这样，“为人民服务”就可以标注为“sbebe”了。4标注不是唯一的标注方式，类似地还有6标注，理论上来说，标注越多会越精细，理论上来说效果也越好，但标注太多也可能存在样本不足的问题，一般常用的就是4标注和6标注。

值得一提的是，这种通过给每个字打标签、进而将问题转化为序列到序列的学习，不仅仅是一种分词方法，还是一种解决大量自然语言问题的思路，比如命名实体识别等任务，同样可以用标注的方法来做。回到分词来，通过字标注法来进行分词的模型有隐马尔科夫模型（HMM）、最大熵模型（ME）、条件随机场模型（CRF），它们在精度上都是递增的，据说目前公开评测中分词效果最好的是4标注的CRF。然而，在本文中，我们要讲解的是最不精确的HMM。因为在我看来，它并非一个特定的模型，而是解决一大类问题的通用思想，一种简化问题的学问。

这一切，还得从概率模型谈起。

点击阅读全文...

对于前面所述的外微分，包括后面还略微涉及到的微分形式的积分，都是纯粹代数定义的内容，本身不具有任何的几何意义。但是，我们可以将某些公式或者定义，与一些几何内容对应起来，使我们更深刻地理解它，并且更灵活运用它。但是，它仅仅是一种对应，而且取决于我们的诠释。比如，我们说外微分公式
$$\int_{\partial D} Pdx+Qdy = \int_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dx\land dy \tag{32} $$
对应于格林公式
$$\int_{\partial D} Pdx+Qdy = \int_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy \tag{33} $$
。这是没问题的，但它们并不等价，它们仅仅是形式上刚好一样。因为格林公式是描述闭合曲线的积分跟面积分的联系，而外微分的公式是一种纯粹的代数运算。因为你完全可以将$dx\land dy$对应于$-dxdy$而不是$dxdy$，这样就得到另外一种几何的对应。

更深刻的问题是：为什么恰好有这个对应？也就是说，为什么经过一些调整和诠释后，就能够得到与积分公式的对应？首先要明确的是外积与普通的数的乘积，除了反对称性之外，是没有任何区别的，因此不少性质得以保留；其次，还应该要回到反对称本身来考虑，矩阵的行列式代表着矩阵所对应的向量组张成的$n$维立体的体积，然而行列式是反对称的，这就意味着反对称运算跟体积、积分等有着先天的联系。当然，更细致的认识，笔者也还没做到。

此外，我们说寻求微分形式的几何意义，通常只是针对不超过3维的空间来讨论的，更高维的几何图像我们很难想象出来，尤其是高维的曲面积分，一般只是类比，但类比是否成立，有时还需要进一步商榷。因此，这种情况下，倒不如干脆点，说微分形式描述的东西就是几何，而不再去寻找所谓的几何意义了。也就是说，反过来，将微分形式和外微分作为公理式的第一性原理来定义几何。

甚至，你可以只将外微分当作是一种记忆各种微分、积分公式的有效途径，比如现在我要大家默写三维空间中的斯托克斯公式，大家估计会乱，因为不一定记得是哪个减哪个。但是在外微分框架下，可以很快地将它推导一遍。好比式$(11)$，如果非要寻求几何解释，那就是开普勒第二定律：单位时间内扫过的面积相等；然而没有几何解释，你依旧可以把方程解下去。

点击阅读全文...