9
Aug
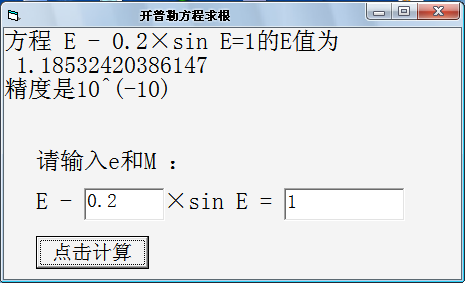
开普勒方程求根器(继续VB,继续拙作..)
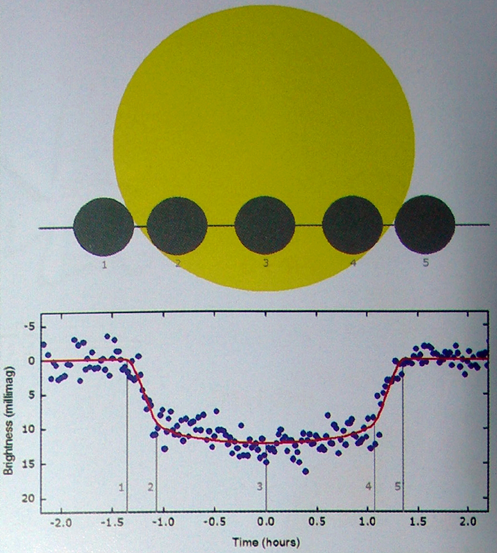
By 苏剑林 | 2010-08-09 | 29593位读者 | 引用
9
Aug
“凌星时刻变化”技术搜寻外行星
By 苏剑林 | 2010-08-09 | 18713位读者 | 引用
11
Aug
谈谈“民科”——兼谈如何推翻爱恩斯坦？
By 苏剑林 | 2010-08-11 | 145002位读者 | 引用
推翻相对论
民科，是“平民科学家”的简称，本来，无论怎么看，这个词都是一个褒义词，代表了一群默默进行科学研究的人，本来，我等天文爱好者都可以用上“民科”这一漂亮词语。然而，“得益于”某些民科（至少在中国是这样的）的狂妄自大，使得“民科”成为了另外一群人的代名词。他们他们从最基础的物理学比如牛顿力学开始，就和正统的物理学分道扬镳。他们使用的专业术语跟正统的物理学都不同。你说东，他说西，以致于民科和专业人士完全不能交流。还有一些民科从易经八卦这些所谓的哲学原理出发，提出一些自以为是的邪乎学说，完全不在物理学的轨道上。这一群人，仿佛自认为自己是救世主，他们就是崭新而又来源已久的新“民科”。由此看，民科和物理学之间存在一个无法沟通的真空。
14
Aug
今天我们都是舟曲人——举国哀悼舟曲遇难同胞
By 苏剑林 | 2010-08-14 | 22533位读者 | 引用
27
Aug
与向量的渊源极深的四元数
By 苏剑林 | 2010-08-27 | 32224位读者 | 引用当我们在使用向量进行几何、物理研究的时候，是否曾经想到：向量竟然起源于“数”？
当向量还没有发展起来的时候（虽然“有方向有大小的量”很早就被人们认识），复数已经得到了认可并且有了初步应用。当我们把复数跟向量联系起来时，我们也许会认为，因为复平面表示的复数运算与向量有着相似之处，才把复数跟几何联系起来。然而事实却相反，向量是从对复数乃至一种称为“四元数”的东西的研究中逐渐分离出来的。换句话说，历史中出现过“四元数”与向量分别研究几何的阶段，麦克斯韦(Maxwell) 将四元 数的数量部分和矢量部分分开，作为 实 体处理，作了大量的矢量分析。三维矢量分析的建立，及同四元数的正式分裂是18世纪80年代由Gibbs和Heaviside独立完成的。矢量代数被推广到矢量函数和矢量微积分，由此开始了四元数和矢量分析的争论，最终矢量分析占了上风。因而“四元数”渐渐离开了教科书。不过，“四元数”的一些特殊而巧妙的应用，仍然使我们不至于忘记它。
26
Aug
最近评论