“Cool Papers + 站内搜索”的一些新尝试
By 苏剑林 | 2024-08-12 | 14782位读者 | 引用在《Cool Papers更新:简单搭建了一个站内检索系统》这篇文章中,我们介绍了Cool Papers新增的站内搜索系统。搜索系统的目的,自然希望能够帮助用户快速找到他们需要的论文。然而,如何高效地检索到对自己有价值的结果,并不是一件简单的事情,这里边往往需要一些技巧,比如精准提炼关键词。
这时候算法的价值就体现出来了,有些步骤人工来做会比较繁琐,但用算法来却很简单。所以接下来,我们将介绍几点通过算法来提高Cool Papers的搜索和筛选论文效率的新尝试。
相关论文
站内搜索背后的技术是全文检索引擎(Full-text Search Engine),简单来说,这就是一个基于关键词匹配的搜索算法,其相似度指标是BM25。
让MathJax更好地兼容谷歌翻译和延时加载
By 苏剑林 | 2024-08-15 | 15503位读者 | 引用很早之前,就有读者提出希望把Cool Papers上面的数学公式渲染一下,因为很多偏数学的论文,它们的摘要甚至标题上都带有LaTeX代码写的数学公式,如果不把这些公式渲染出来,那么看上去就像是一堆乱码,确实会比较影响阅读体验。然而,之前的测试显示,负责渲染公式的MathJax跟谷歌翻译和延时加载都不大兼容,所以尽管需求存在已久,但笔者一直没有把它加上去。
不过好消息是,经过反复查阅和调试,这两天笔者总算把兼容性问题解决了,所以现在大家看到的Cool Papers已经能够渲染数学公式了。这篇文章总结一下解决方案,供大家参考。
低秩近似之路(二):SVD
By 苏剑林 | 2024-10-01 | 11530位读者 | 引用上一篇文章中我们介绍了“伪逆”,它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$(或$\boldsymbol{B}$)时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解,即
\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了,这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似(秩不超过$r$的最优近似)”。而要解决这个问题,就需要请出大名鼎鼎的“SVD(奇异值分解)”了。虽然本系列把伪逆作为开篇,但它的“名声”远不如SVD,听过甚至用过SVD但没听说过伪逆的应该大有人在,包括笔者也是先了解SVD后才看到伪逆。
接下来,我们将围绕着矩阵的最优低秩近似来展开介绍SVD。
结论初探
对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$,都可以找到如下形式的奇异值分解(SVD,Singular Value Decomposition):
\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}
近乎完美地解决MathJax与Marked的冲突
By 苏剑林 | 2024-08-26 | 11749位读者 | 引用在《让MathJax更好地兼容谷歌翻译和延时加载》我们提到Cool Papers加入了MathJax来解析LaTeX公式,不过万万没想到引发了诸多兼容性问题,虽然部分问题纯粹是笔者的强迫症作祟,但一个尽可能完美的解决方案终究是让人赏心悦目的,所以还是愿意在上面花一点心思。
上一篇文章我们已经解决了MathJax与谷歌翻译、延时加载的兼容性,这篇文章我们则来解决MathJax与Marked的冲突。
问题简述
Markdown是一种轻量级标记语言,允许人们使用易读易写的纯文本格式编写文档,可谓是目前最流行的写作语法之一,Cool Papers中的[Kimi]功能,基本上也是按照Markdown语法输出。然而。Markdown并不是直接面向浏览器的语言,面向浏览器的语言叫做HTML,所以在展示给用户之前,有一个Markdown转HTML的过程(渲染)。
“闭门造车”之多模态思路浅谈(三):位置编码
By 苏剑林 | 2024-09-06 | 30915位读者 | 引用在前面的文章中,我们曾表达过这样的观点:多模态LLM相比纯文本LLM的主要差异在于,前者甚至还没有形成一个公认为标准的方法论。这里的方法论,不仅包括之前讨论的生成和训练策略,还包括一些基础架构的设计,比如本文要谈的“多模态位置编码”。
对于这个主题,我们之前在《Transformer升级之路:17、多模态位置编码的简单思考》就已经讨论过一遍,并且提出了一个方案(RoPE-Tie)。然而,当时笔者对这个问题的思考仅处于起步阶段,存在细节考虑不周全、认识不够到位等问题,所以站在现在的角度回看,当时所提的方案与完美答案还有明显的距离。
因此,本文我们将自上而下地再次梳理这个问题,并且给出一个自认为更加理想的结果。
多模位置
多模态模型居然连位置编码都没有形成共识,这一点可能会让很多读者意外,但事实上确实如此。对于文本LLM,目前主流的位置编码是RoPE(RoPE就不展开介绍了,假设读者已经熟知),更准确来说是RoPE-1D,因为原始设计只适用于1D序列。后来我们推导了RoPE-2D,这可以用于图像等2D序列,按照RoPE-2D的思路我们可以平行地推广到RoPE-3D,用于视频等3D序列。
Decoder-only的LLM为什么需要位置编码?
By 苏剑林 | 2024-09-01 | 25278位读者 | 引用众所周知,目前主流的LLM,都是基于Causal Attention的Decoder-only模型(对此我们在《为什么现在的LLM都是Decoder-only的架构?》也有过相关讨论),而对于Causal Attention,已经有不少工作表明它不需要额外的位置编码(简称NoPE)就可以取得非平凡的结果。然而,事实是主流的Decoder-only LLM都还是加上了额外的位置编码,比如RoPE、ALIBI等。
那么问题就来了:明明说了不加位置编码也可以,为什么主流的LLM反而都加上了呢?不是说“多一事不如少一事”吗?这篇文章我们从三个角度给出笔者的看法:
1、位置编码对于Attention的作用是什么?
2、NoPE的Causal Attention是怎么实现位置编码的?
3、NoPE实现的位置编码有什么不足?
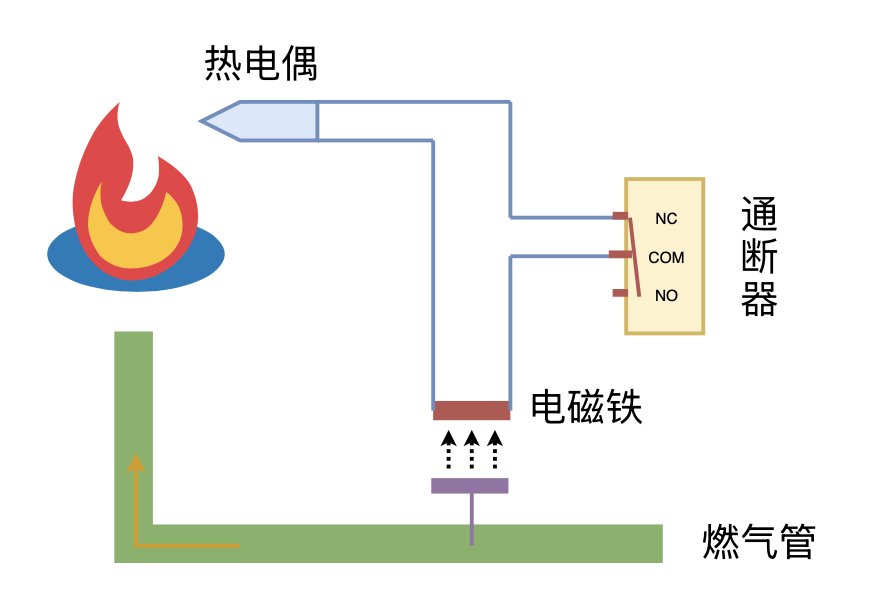
利用“熄火保护 + 通断器”实现燃气灶智能关火
By 苏剑林 | 2024-09-26 | 12002位读者 | 引用低秩近似之路(四):ID
By 苏剑林 | 2024-10-30 | 4414位读者 | 引用这篇文章的主角是ID(Interpolative Decomposition),中文可以称之为“插值分解”,它同样可以理解为是一种具有特定结构的低秩分解,其中的一侧是该矩阵的若干列(当然如果你偏好于行,那么选择行也没什么问题),换句话说,ID试图从一个矩阵中找出若干关键列作为“骨架”(通常也称作“草图”)来逼近原始矩阵。
可能很多读者都未曾听说过ID,即便维基百科也只有几句语焉不详的介绍(链接),但事实上,ID跟SVD一样早已内置在SciPy之中(参考scipy.linalg.interpolative),这侧面印证了ID的实用价值。
基本定义
前三篇文章我们分别介绍了伪逆、SVD、CR近似,它们都可以视为寻找特定结构的低秩近似:
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\end{equation}









最近评论