科学空间|Scientific Spaces

在将近三年前的百度“2019语言与智能技术竞赛”（下称LIC2019）中，笔者提出了一个新的关系抽取模型（参考《基于DGCNN和概率图的轻量级信息抽取模型》），后被进一步发表和命名为“CasRel”，算是当时关系抽取的SOTA。然而，CasRel提出时笔者其实也是首次接触该领域，所以现在看来CasRel仍有诸多不完善之处，笔者后面也有想过要进一步完善它，但也没想到特别好的设计。

后来，笔者提出了GlobalPointer以及近日的Efficient GlobalPointer，感觉有足够的“材料”来构建新的关系抽取模型了。于是笔者从概率图思想出发，参考了CasRel之后的一些SOTA设计，最终得到了一版类似TPLinker的模型。

基础思路

关系抽取乍看之下是三元组$(s,p,o)$（即subject, predicate, object)的抽取，但落到具体实现上，它实际是“五元组”$(s_h,s_t,p,o_h,o_t)$的抽取，其中$s_h,s_t$分别是$s$的首、尾位置，而$o_h,o_t$则分别是$o$的首、尾位置。

点击阅读全文...

多任务学习是一个很宽泛的命题，不同场景下多任务学习的目标不尽相同。在《多任务学习漫谈（一）：以损失之名》和《多任务学习漫谈（二）：行梯度之事》中，我们将多任务学习的目标理解为“做好每一个任务”，具体表现是“尽量平等地处理每一个任务”，我们可以称之为“平行型多任务学习”。然而，并不是所有多任务学习的目标都是如此，在很多场景下，我们主要还是想学好某一个主任务，其余任务都只是辅助，希望通过增加其他任务的学习来提升主任务的效果罢了，此类场景我们可以称为“主次型多任务学习”。

在这个背景下，如果还是沿用平行型多任务学习的“做好每一个任务”的学习方案，那么就可能会明显降低主任务的效果了。所以本文继续沿着“行梯度之事”的想法，探索主次型多任务学习的训练方案。

目标形式

在这篇文章中，我们假设读者已经阅读并且基本理解《多任务学习漫谈（二）：行梯度之事》里边的思想和方法，那么在梯度视角下，让某个损失函数保持下降的必要条件是更新量与其梯度夹角至少大于90度，这是贯穿全文的设计思想。

点击阅读全文...

大约两年前，笔者在百度的“2020语言与智能技术竞赛”中首次接触到了事件抽取任务，并在文章《bert4keras在手，baseline我有：百度LIC2020》中分享了一个转化为BERT+CRF做NER的简单baseline。不过，当时的baseline更像是一个用来凑数的半成品，算不上一个完整的事件抽取模型。而这两年来，关系抽取的模型层见迭出，SOTA一个接一个，但事件抽取似乎没有多亮眼的设计。

最近笔者重新尝试了事件抽取任务，在之前的关系抽取模型GPLinker的基础上，结合完全子图搜索，设计一个比较简单但相对完备的事件联合抽取模型，依然称之为GPLinker，在此请大家点评一番。

任务简介

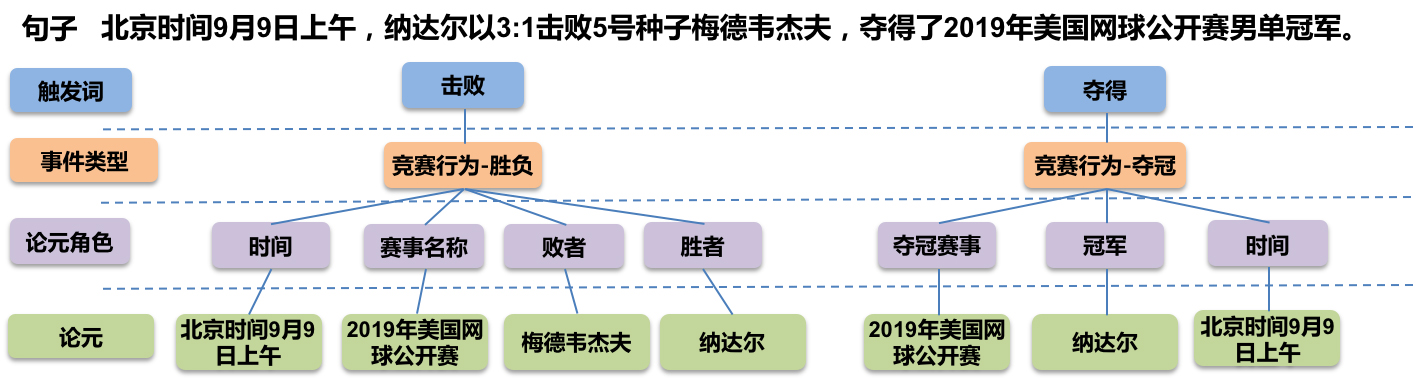
事件抽取是一个比较综合的任务。一个标准的事件抽取样本如下：

标准的事件抽取样本（图片来自百度DuEE的GitHub）

点击阅读全文...

高效Transformer，泛指所有概率Transformer效率的工作，笔者算是关注得比较早了，最早的博客可以追溯到2019年的《为节约而生：从标准Attention到稀疏Attention》，当时做这块的工作很少。后来，这类工作逐渐多了，笔者也跟进了一些，比如线性Attention、Performer、Nyströmformer，甚至自己也做了一些探索，比如之前的“Transformer升级之路”。再后来，相关工作越来越多，但大多都很无趣，所以笔者就没怎么关注了。

本文模型脉络图

大抵是“久旱逢甘霖”的感觉，最近终于出现了一个比较有意思的高效Transformer工作——来自Google的《Transformer Quality in Linear Time》，经过细读之后，笔者认为论文里边真算得上是“惊喜满满”了～

点击阅读全文...

众所周知，现在的Transformer越做越大，但这个“大”通常是“宽”而不是“深”，像GPT-3虽然参数有上千亿，但也只是一个96层的Transformer模型，与我们能想象的深度相差甚远。是什么限制了Transformer往“深”发展呢？可能有的读者认为是算力，但“宽而浅”的模型所需的算力不会比“窄而深”的模型少多少，所以算力并非主要限制，归根结底还是Transformer固有的训练困难。一般的观点是，深模型的训练困难源于梯度消失或者梯度爆炸，然而实践显示，哪怕通过各种手段改良了梯度，深模型依然不容易训练。

近来的一些工作（如Admin）指出，深模型训练的根本困难在于“增量爆炸”，即模型越深对输出的扰动就越大。上周的论文《DeepNet: Scaling Transformers to 1,000 Layers》则沿着这个思路进行尺度分析，根据分析结果调整了模型的归一化和初始化方案，最终成功训练出了1000层的Transformer模型。整个分析过程颇有参考价值，我们不妨来学习一下。

增量爆炸

原论文的完整分析比较长，而且有些假设或者描述细酌之下是不够合理的。所以在本文的分享中，笔者会尽量修正这些问题，试图以一个更合理的方式来得到类似结果。

点击阅读全文...

大概在1年前，我们提出了旋转位置编码（RoPE），并发布了对应的预训练模型RoFormer。随着时间的推移，RoFormer非常幸运地得到了越来越多的关注和认可，比如EleutherAI新发布的60亿和200亿参数的GPT模型中就用上了RoPE位置编码，Google新提出的FLASH模型论文中则明确指出了RoPE对Transformer效果有明显的提升作用。

与此同时，我们也一直在尝试继续加强RoFormer模型，试图让RoFormer的性能“更上一层楼”。经过近半年的努力，我们自认为取得了还不错的成果，因此将其作为“RoFormerV2”正式发布：

Github：https://github.com/ZhuiyiTechnology/roformer-v2

点击阅读全文...

之前笔者一直都是聚焦于模型的构思和实现，鲜有关注模型的训练加速，像混合精度和XLA这些技术，虽然也有听过，但没真正去实践过。这两天折腾了一番，成功在bert4keras中使用了混合精度和XLA来加速训练，在此做个简单的总结，供大家参考。

本文的多数经验结论并不只限于bert4keras中使用，之所以在标题中强调bert4keras，只不过bert4keras中的模型实现相对较为规整，因此启动这些加速技巧所要做的修改相对更少。

实验环境

本文的实验显卡为3090，使用的docker镜像为nvcr.io/nvidia/tensorflow:21.09-tf1-py3，其中自带的tensorflow版本为1.15.5。另外，实验所用的bert4keras版本为0.11.3。其他环境也可以参考着弄，要注意有折腾精神，不要指望着无脑调用。

顺便提一下，3090、A100等卡只能用cuda11，而tensorflow官网的1.15版本是不支持cuda11的，如果还想用tensorflow 1.x，那么只能用nvidia亲自维护的nvidia-tensorflow，或者用其构建的docker镜像。用nvidia而不是google维护的tensorflow，除了能让你在最新的显卡用上1.x版本外，还有nvidia专门做的一些额外优化，具体文档可以参考这里。

点击阅读全文...

不知道大家留意到一个细节没有，就是当前NLP主流的预训练模式都是在一个固定长度（比如512）上进行，然后直接将预训练好的模型用于不同长度的任务中。大家似乎也没有对这种模式有过怀疑，仿佛模型可以自动泛化到不同长度是一个“理所应当”的能力。

当然，笔者此前同样也没有过类似的质疑，直到前几天笔者做了Base版的GAU实验后才发现GAU的长度泛化能力并不如想象中好。经过进一步分析后，笔者才明白原来这种长度泛化的能力并不是“理所当然”的......

模型回顾

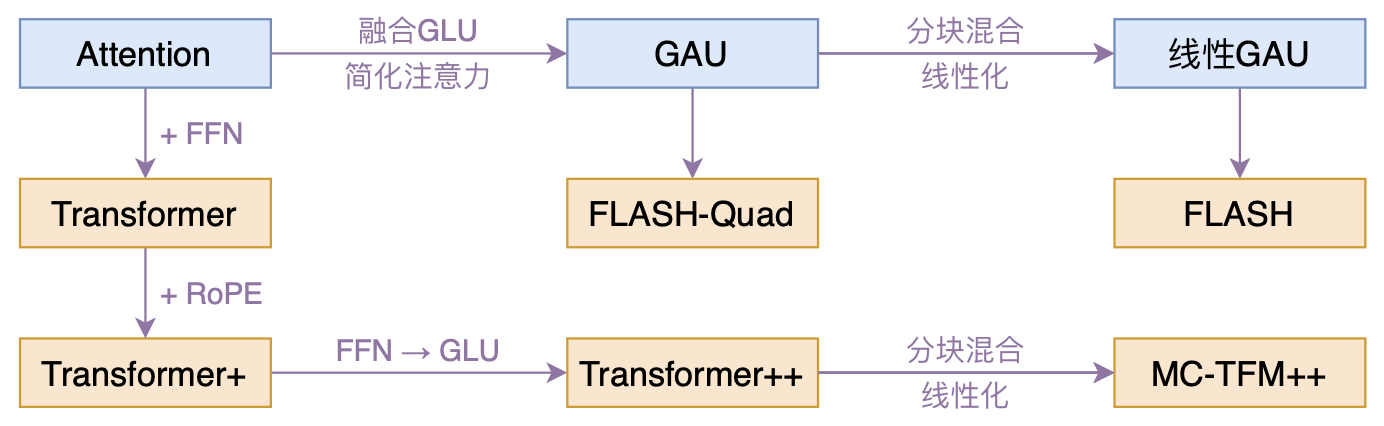
在《FLASH：可能是近来最有意思的高效Transformer设计》中，我们介绍了“门控注意力单元GAU”，它是一种融合了GLU和Attention的新设计。

除了效果，GAU在设计上给我们带来的冲击主要有两点：一是它显示了单头注意力未必就逊色于多头注意力，这奠定了它“快”、“省”的地位；二是它是显示了注意力未必需要Softmax归一化，可以换成简单的$\text{relu}^2$除以序列长度：
\begin{equation}\boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right)\end{equation}

点击阅读全文...