2
Mar
三味Capsule：矩阵Capsule与EM路由
By 苏剑林 | 2018-03-02 | 215423位读者 | 引用事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。
大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？
在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。
论文摘要
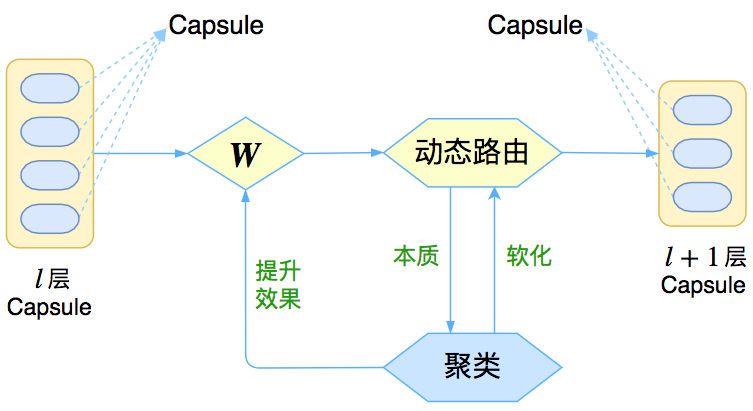
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图
Capsule框架的简明示意图
这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：
1、原来用向量来表示一个Capsule，现在用矩阵来表示；
2、聚类算法换成了GMM（高斯混合模型）；
3、在实验部分，实现了Capsule版的卷积。
28
Mar
变分自编码器（二）：从贝叶斯观点出发
By 苏剑林 | 2018-03-28 | 465490位读者 | 引用源起
前几天写了博文《变分自编码器（一）：原来是这么一回事》，从一种比较通俗的观点来理解变分自编码器（VAE），在那篇文章的视角中，VAE跟普通的自编码器差别不大，无非是多加了噪声并对噪声做了约束。然而，当初我想要弄懂VAE的初衷，是想看看究竟贝叶斯学派的概率图模型究竟是如何与深度学习结合来发挥作用的，如果仅仅是得到一个通俗的理解，那显然是不够的。
所以我对VAE继续思考了几天，试图用更一般的、概率化的语言来把VAE说清楚。事实上，这种思考也能回答通俗理解中无法解答的问题，比如重构损失用MSE好还是交叉熵好、重构损失和KL损失应该怎么平衡，等等。
建议在阅读《变分自编码器（一）：原来是这么一回事》后对本文进行阅读，本文在内容上尽量不与前文重复。
准备
在进入对VAE的描述之前，我觉得有必要把一些概念性的内容讲一下。
11
May
【致敬】费曼诞辰100年
By 苏剑林 | 2018-05-11 | 30896位读者 | 引用
18
May
简明条件随机场CRF介绍（附带纯Keras实现）
By 苏剑林 | 2018-05-18 | 328211位读者 | 引用笔者去年曾写过博文《果壳中的条件随机场(CRF In A Nutshell)》，以一种比较粗糙的方式介绍了一下条件随机场（CRF）模型。然而那篇文章显然有很多不足的地方，比如介绍不够清晰，也不够完整，还没有实现，在这里我们重提这个模型，将相关内容补充完成。
本文是对CRF基本原理的一个简明的介绍。当然，“简明”是相对而言中，要想真的弄清楚CRF，免不了要提及一些公式，如果只关心调用的读者，可以直接移到文末。
图示
按照之前的思路，我们依旧来对比一下普通的逐帧softmax和CRF的异同。
逐帧softmax
CRF主要用于序列标注问题，可以简单理解为是给序列中的每一帧都进行分类，既然是分类，很自然想到将这个序列用CNN或者RNN进行编码后，接一个全连接层用softmax激活，如下图所示
逐帧softmax并没有直接考虑输出的上下文关联
21
May
厨房，菜市场，其实都是武林
By 苏剑林 | 2018-05-21 | 40093位读者 | 引用
30
May
最小熵原理（三）：“飞象过河”之句模版和语言结构
By 苏剑林 | 2018-05-30 | 59639位读者 | 引用在前一文《最小熵原理（二）：“当机立断”之词库构建》中，我们以最小熵原理为出发点进行了一系列的数学推导，最终得到$(2.15)$和$(2.17)$式，它告诉我们两个互信息比较大的元素我们应该将它们合并起来，这有利于降低“学习难度”。于是利用这一原理，我们通过邻字互信息来实现了词库的无监督生成。
由字到词、由词到词组，考察的是相邻的元素能不能合并成一个好“套路”。可是套路为什么非得要相邻的呢？当然不一定相邻，我们学习语言的时候，不仅仅会学习到词语、词组，还要学习到“固定搭配”，也就是说词语怎么运用才是合理的，这是语法的体现，是本文所要探究的，希望最终能达到一定的无监督句法分析的效果。
由于这次我们考虑的是跨邻词的语言关联，因此我给它起个名字为“飞象过河”，正是
“套路宝典”第二式——“飞象过河”
语言结构
对于大多数人来说，并不会真正知道什么是语法，他们脑海里就只有一些“固定搭配”、“定式”，或者更正式一点可以叫“模版”。大多数情况下，我们是根据模版来说出合理的话来。而不同的人的说话模版可能有所不同，这就是个人的说话风格，甚至是“口头禅”。
13
Jun
“噪声对比估计”杂谈：曲径通幽之妙
By 苏剑林 | 2018-06-13 | 176117位读者 | 引用说到噪声对比估计，或者“负采样”，大家可能立马就想到了Word2Vec。事实上，它的含义远不止于此，噪音对比估计（NCE, Noise Contrastive Estimation）是一个迂回但却异常精美的技巧，它使得我们在没法直接完成归一化因子（也叫配分函数）的计算时，就能够去估算出概率分布的参数。本文就让我们来欣赏一下NCE的曲径通幽般的美妙。
注：由于出发点不同，本文所介绍的“噪声对比估计”实际上更偏向于所谓的“负采样”技巧，但两者本质上是一样的，在此不作区分。
问题起源
问题的根源是难分难舍的指数概率分布～
指数族分布
在很多问题中都会出现指数族分布，即对于某个变量$\boldsymbol{x}$的概率$p(\boldsymbol{x})$，我们将其写成
$$p(\boldsymbol{x}) = \frac{e^{G(\boldsymbol{x})}}{Z}\tag{1}$$
其中$G(\boldsymbol{x})$是$\boldsymbol{x}$的某个“能量”函数，而$Z=\sum_{\boldsymbol{x}} e^{G(\boldsymbol{x})}$则是归一化常数，也叫配分函数。这种分布也称为“玻尔兹曼分布”。
10
Oct
变分自编码器 = 最小化先验分布 + 最大化互信息
By 苏剑林 | 2018-10-10 | 125796位读者 | 引用这篇文章很简短，主要描述的是一个很有用、也不复杂、但是我居然这么久才发现的事实～
在《深度学习的互信息：无监督提取特征》一文中，我们通过先验分布和最大化互信息两个loss的加权组合来得到Deep INFOMAX模型最后的loss。在那篇文章中，虽然把故事讲完了，但是某种意义上来说，那只是个拼凑的loss。而本文则要证明那个loss可以由变分自编码器自然地导出来。
过程
不厌其烦地重复一下，变分自编码器（VAE）需要优化的loss是
\begin{equation}\begin{aligned}&KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))\\
=&\iint \tilde{p}(x)p(z|x)\log \frac{\tilde{p}(x)p(z|x)}{q(x|z)q(z)} dzdx\end{aligned}\end{equation}
相关的论述在本博客已经出现多次了。VAE中既包含编码器，又包含解码器，如果我们只需要编码特征，那么再训练一个解码器就显得很累赘了。所以重点是怎么将解码器去掉。
其实再简单不过了，把VAE的loss分开两部分
最近评论