4
Feb
400多本数学电子书籍（供下载）
By 苏剑林 | 2010-02-04 | 79031位读者 | 引用转自：http://bbs.emath.ac.cn/redirect.php?tid=1989
来源：http://cid-ec227156e4cad4ab.profile.live.com/
不论是对于学习高等数学还是初中数学，里面都有不少数学精品。BoJone一发现，便用Thunder下了一大堆（正好满足了我加强“数学分析”的需要），并立即与大家分享了。资源储存在微软的网盘，按常理来说不存在链接失效的问题，不过BoJone建议需要的读者还是尽快下载到自己的电脑上，毕竟这样更加保险，因为或许哪一天作者不愿意共享了，那就“走宝”了，呵呵。
24
Apr
用RecomposIt简单给图片换背景
By 苏剑林 | 2010-04-24 | 26704位读者 | 引用
14
Mar
庆祝圆周率(π)节！
By 苏剑林 | 2010-03-14 | 70497位读者 | 引用
在圆周率日当天，滑铁卢大学会以供应免费的馅饼当庆祝。
π = 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 ...
$\pi \approx {355}/{113}$
“山巅一寺一壶酒，尔乐苦煞吾，把酒吃，酒杀尔，杀不死，乐而乐”
$\pi$，一个小小的符号，代表着一个伟大的数字。从古到今，几乎所有国家都有人研究过它。在很长的时期内，$\pi$的有效数字代表了这个国家的数学发展程度，在使用计算机计算以前，$\pi$的计算可谓是马拉松式进行。很早人们就知道了2-4位的有效数字（古希腊、古中国、古印度），众所周知之后祖冲之的3.1415926领先了一千多年；紧接着是西方的35位、100位、500位.....甚至有人穷其一生就为算$\pi$！自从计算机参与到其中之后，有效数字光速般增加，而在2009年末，有科学家已经用超级计算机计算出圆周率暂时计到小数点后2万9千亿个小数位。现在$\pi$的位数已经不大重要了（毕竟30位有效数字就完全足够用来精确衡量宇宙大小！），$\pi$的计算成为了测试计算机性能以及测试算法效率的一个指标！
17
Apr
Lamost被冠名为“郭守敬望远镜”
By 苏剑林 | 2010-04-17 | 51995位读者 | 引用
23
Mar
谷歌搜索退出中国内地
By 苏剑林 | 2010-03-23 | 20351位读者 | 引用站长：Google终究还是退出了中国...当然，我们依旧能够使用它，尽管以后也许对中文的支持不会那么好。但是，值得思考的是，这是Google的RP问题，还是中国的政策问题？
北京时间3月23日凌晨3时零3分，谷歌公司高级副总裁、首席法律官大卫·德拉蒙德德(David Drummond)在一个博客中公开发表声明，宣布停止对谷歌中国搜索服务的“过滤审查”，并将搜索服务由中国内地转至香港。
他表示，登录google.cn的中国内地用户将被自动导向谷歌香港页面，使用服务器设在香港的未经审查的谷歌搜索(Google Search)、谷歌新闻(Google News)和谷歌图片(Google Images)服务。
声明还表示，谷歌公司并不会撤出中国内地，将保留在中国的销售和研发业务，保留未经审查的谷歌地图(Google Maps)等服务。谷歌600名中国雇员的去向仍未确定，他们有可能会被改派。
23
Mar
【通知转载】国家天文台信息技术类人才招聘
By 苏剑林 | 2010-03-23 | 17162位读者 | 引用文章来源：国家天文台
国家天文台LAMOST大科学工程面向全社会招聘信息技术类人才若干名，主要从事数据密集型天文学研究、数据库设计开发、天文应用软件服务开发、数据处理、数据挖掘、数值模拟、高性能计算、算法优化、网站网页设计维护、天文数据整理与管理、网络科普教育等工作。大天区面积多目标光纤光谱天文望远镜（LAMOST）是一项国家重大科学工程项目。该工程项目于2008年底竣工，2009年6月通过国家验收，正处于观测试运行阶段。LAMOST天文望远镜是我国已建成的最大、最先进的天文观测设备，是世界上光谱观测效率最高的望远镜，4米口径5度视场，每次可观测4000个目标，每晚可观测数万个目标，获得数十GB的数据，每年可获得数TB的科学数据。如何处理、分析、管理、发布、挖掘如此海量的数据，就是诚聘的上述人才所要面临的挑战。
4
Apr
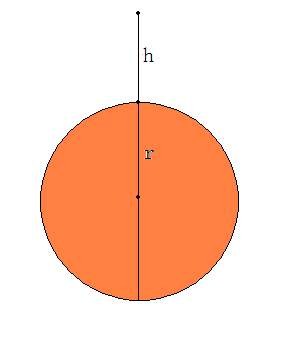
关于自由落体公式的简单修正
By 苏剑林 | 2010-04-04 | 66746位读者 | 引用
自由落体公式-示意图
自由落体的一般定义是：只考虑吸引天体和被吸引天体的引力因素，忽略其他的运动和大气摩擦等因素，物体从静止（相对于吸引天体）开始接近吸引天体的运动。根据这个定义，假设地球为一个均匀球体，半径为r，质量为M，物体从距离地表h高度处自由落下。求落到地面的时间t，或者根据时间t求h。
令s为t时刻物体左右下落的物体与地表的距离，忽略物体的小质量，那么可以列出微分方程：
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$并且初始条件是$t=0,s=h,\dot{s}=v=0$
在实际应用中，我们不必求出这道微分方程的精确解，因为这个解极其麻烦，在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。
18
Apr
最近评论