不用L约束又不会梯度消失的GAN,了解一下?
By 苏剑林 | 2018-11-20 | 169010位读者 | 引用不知道从什么时候开始,我发现我也掉到了GAN的大坑里边了,唉,争取早日能跳出来...
这篇博客介绍的是我最近提交到arxiv的一个关于GAN的新框架,里边主要介绍了一种对概率散度的新理解,并且基于这种理解推导出了一个新的GAN。整篇文章比较偏理论,对这个GAN的相关性质都做了完整的论证,自认为是一个理论完备的结果。
文章链接:https://papers.cool/arxiv/1811.07296
先摆结论:
1、论文提供了一种分析和构造概率散度的直接思路,从而简化了构建新GAN框架的过程。
2、推导出了一个称为GAN-QP的GAN框架$\eqref{eq:gan-gp-gd}$,这个GAN不需要像WGAN那样的L约束,又不会有SGAN的梯度消失问题,实验表明它至少有不逊色于、甚至优于WGAN的表现。
论文的实验最大做到了512x512的人脸生成(CelebA HQ),充分表明了模型的有效性(效果不算完美,但是模型特别简单)。有兴趣的朋友,欢迎继续阅读下去。
最小熵原理(四):“物以类聚”之从图书馆到词向量
By 苏剑林 | 2018-12-02 | 92219位读者 | 引用从第一篇看下来到这里,我们知道所谓“最小熵原理”就是致力于降低学习成本,试图用最小的成本完成同样的事情。所以整个系列就是一个“偷懒攻略”。那偷懒的秘诀是什么呢?答案是“套路”,所以本系列又称为“套路宝典”。
本篇我们介绍图书馆里边的套路。
先抛出一个问题:词向量出现在什么时候?是2013年Mikolov的Word2Vec?还是是2003年Bengio大神的神经语言模型?都不是,其实词向量可以追溯到千年以前,在那古老的图书馆中...
走进图书馆
图书馆里有词向量?还是千年以前?在哪本书?我去借来看看。
放书的套路
其实不是哪本书,而是放书的套路。
很明显,图书馆中书的摆放是有“套路”的:它们不是随机摆放的,而是分门别类地放置的,比如数学类放一个区,文学类放一个区,计算机类也放一个区;同一个类也有很多子类,比如数学类中,数学分析放一个子区,代数放一个子区,几何放一个子区,等等。读者是否思考过,为什么要这么分类放置?分类放置有什么好处?跟最小熵又有什么关系?
VQ-VAE的简明介绍:量子化自编码器
By 苏剑林 | 2019-06-24 | 310424位读者 | 引用印象中很早之前就看到过VQ-VAE,当时对它并没有什么兴趣,而最近有两件事情重新引起了我对它的兴趣。一是VQ-VAE-2实现了能够匹配BigGAN的生成效果(来自机器之心的报道);二是我最近看一篇NLP论文《Unsupervised Paraphrasing without Translation》时发现里边也用到了VQ-VAE。这两件事情表明VQ-VAE应该是一个颇为通用和有意思的模型,所以我决定好好读读它。
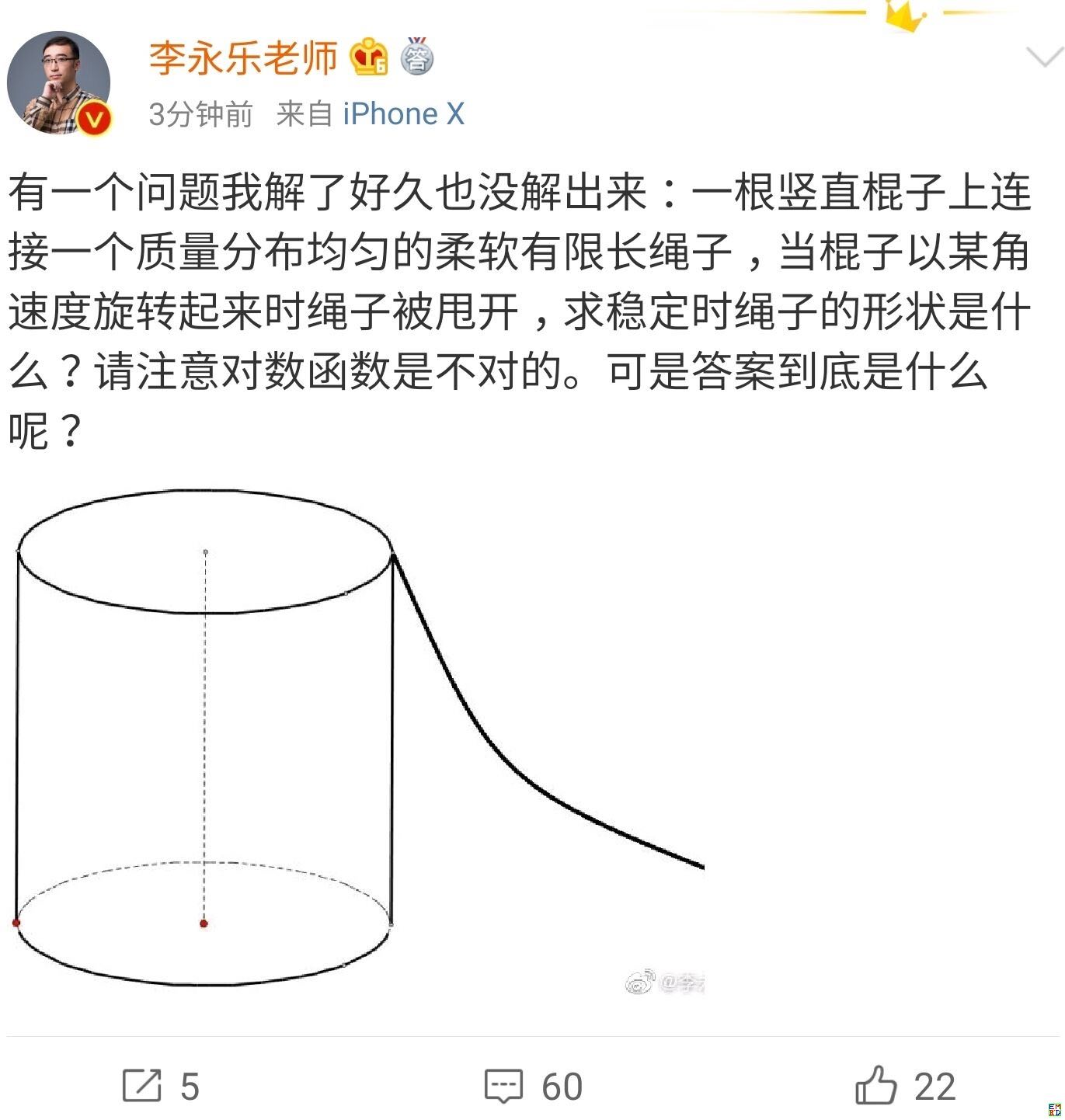
你跳绳的时候,想过绳子的形状曲线是怎样的吗?
By 苏剑林 | 2019-07-06 | 48773位读者 | 引用从采样看优化:可导优化与不可导优化的统一视角
By 苏剑林 | 2020-06-23 | 54865位读者 | 引用不少读者都应该知道,损失函数与评测指标的不一致性是机器学习的典型现象之一,比如分类问题中损失函数用交叉熵,评测指标则是准确率或者F1,又比如文本生成中损失函数是teacher-forcing形式的交叉熵,评测指标则是BLEU、ROUGE等。理想情况下,当然是评测什么指标,我们就去优化这个指标,然而评测指标通常都是不可导的,而我们多数都是使用基于梯度的优化器,这就要求最小化的目标必须是可导的,这是不一致性的来源。
前些天在arxiv刷到了一篇名为《MLE-guided parameter search for task loss minimization in neural sequence modeling》的论文,顾名思义,它是研究如何直接优化文本生成的评测指标的。经过阅读,笔者发现这篇论文很有价值,事实上它提供了一种优化评测指标的新思路,适用范围并不局限于文本生成中。不仅如此,它甚至还包含了一种理解可导优化与不可导优化的统一视角。
采样视角
首先,我们可以通过采样的视角来重新看待优化问题:设模型当前参数为$\theta$,优化目标为$l(\theta)$,我们希望决定下一步的更新量$\Delta\theta$,为此,我们先构建分布
\begin{equation}p(\Delta\theta|\theta)=\frac{e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha}}{Z(\theta)},\quad Z(\theta) = \int e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha} d(\Delta\theta)\end{equation}
强大的NVAE:以后再也不能说VAE生成的图像模糊了
By 苏剑林 | 2020-07-10 | 106621位读者 | 引用昨天早上,笔者在日常刷arixv的时候,然后被一篇新出来的论文震惊了!论文名字叫做《NVAE: A Deep Hierarchical Variational Autoencoder》,顾名思义是做VAE的改进工作的,提出了一个叫NVAE的新模型。说实话,笔者点进去的时候是不抱什么希望的,因为笔者也算是对VAE有一定的了解,觉得VAE在生成模型方面的能力终究是有限的。结果,论文打开了,呈现出来的画风是这样的:
然后笔者的第一感觉是这样的:
W!T!F! 这真的是VAE生成的效果?这还是我认识的VAE么?看来我对VAE的认识还是太肤浅了啊,以后再也不能说VAE生成的图像模糊了...
生成扩散模型漫谈(二):DDPM = 自回归式VAE
By 苏剑林 | 2022-07-06 | 122090位读者 | 引用在文章《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中,我们为生成扩散模型DDPM构建了“拆楼-建楼”的通俗类比,并且借助该类比完整地推导了生成扩散模型DDPM的理论形式。在该文章中,我们还指出DDPM本质上已经不是传统的扩散模型了,它更多的是一个变分自编码器VAE,实际上DDPM的原论文中也是将它按照VAE的思路进行推导的。
所以,本文就从VAE的角度来重新介绍一版DDPM,同时分享一下自己的Keras实现代码和实践经验。
Github地址:https://github.com/bojone/Keras-DDPM
多步突破
在传统的VAE中,编码过程和生成过程都是一步到位的:
\begin{equation}\text{编码:}\,\,x\to z\,,\quad \text{生成:}\,\,z\to x\end{equation}
生成扩散模型漫谈(十三):从万有引力到扩散模型
By 苏剑林 | 2022-10-18 | 51722位读者 | 引用对于很多读者来说,生成扩散模型可能是他们遇到的第一个能够将如此多的数学工具用到深度学习上的模型。在这个系列文章中,我们已经展示了扩散模型与数学分析、概率统计、常微分方程、随机微分方程乃至偏微分方程等内容的深刻联系,可以说,即便是做数学物理方程的纯理论研究的同学,大概率也可以在扩散模型中找到自己的用武之地。
在这篇文章中,我们再介绍一个同样与数学物理有深刻联系的扩散模型——由“万有引力定律”启发的ODE式扩散模型,出自论文《Poisson Flow Generative Models》(简称PFGM),它给出了一个构建ODE式扩散模型的全新视角。
万有引力
中学时期我们就学过万有引力定律,大概的描述方式是:
两个质点彼此之间相互吸引的作用力,是与它们的质量乘积成正比,并与它们之间的距离成平方反比。












最近评论