科学空间|Scientific Spaces

前段时间天池出了个天文数据挖掘竞赛——LAMOST光谱分类（将对应的光谱识别为4类中的一类），虽然没有奖金，但还是觉得挺有意思，所以就报名参加了。做了一段时间，成绩自我感觉还可以，然而最后我却忘记了（或者说根本就没留意到）初赛最后两天还有一步是提交新的测试集结果，然后就没有然后了，留下了一个未竟的模型，可谓“出师未捷身先死”，还是被自己弄死的～

天文数据挖掘大赛——天体光谱智能分类

后来跟其他参赛选手讨论了一下，发现其实我的这个模型还是不错的。当时我记得初赛第一名的成绩是0.83+，而我当时的成绩是0.82+，排名大概是第4、5左右，而且据说很多分数在0.8+的队伍都已经使用了融合模型，而我这0.82+的成绩仅仅是单模型的结果～在平时的群聊中发现也有不少朋友在做一维序列分类模型，而光谱分类本质上也就是一个一维的序列分类，所以分享一下模型，估计对相关朋友会有一定的参考价值。

模型

事实上也不是什么特别的模型，就是普通的一维卷积加残差，对于熟悉图像处理的朋友，这实在是再普通不过的结构了。

点击阅读全文...

前几日写了一篇VAE的通俗解读，也得到了一些读者的认可。然而，你是否厌倦了每次介绍都只有一个MNIST级别的demo？不要急，这就给大家带来一个更经典的VAE玩具：机器人作诗。

为什么说“更经典”呢？前一篇文章我们说过用VAE生成的图像相比GAN生成的图像会偏模糊，也就是在图像这一“仗”上，VAE是劣势。然而，在文本生成这一块上，VAE却漂亮地胜出了。这是因为GAN希望把判别器（度量）也直接训练出来，然而对于文本来说，这个度量很可能是离散的、不可导的，因此纯GAN就很难训练了。而VAE中没有这个步骤，它是通过重构输入来完成的，这个重构过程对于图像还是文本都可以进行。所以，文本生成这件事情，对于VAE来说它就跟图像生成一样，都是一个基本的、直接的应用；对于（目前的）GAN来说，却是艰难的象征，是它挥之不去的“心病”。

嗯，古有曹植七步作诗，今有VAE随机成诗，让我们开始吧～

模型

对于很多人来说，诗是一个很美妙的玩意，美妙之处在于大多数人都不真正懂得诗，但大家对诗的模样又有一知半解的认识。因此，只要生成的“诗”稍微像模像样一点，我们通常都会认为机器人可以作诗了。因此，所谓作诗机器人，是一个纯粹的玩具了，能作几句诗，也不意味着普通语言的生成能力有多好，也不意味着我们对NLP的理解有多深。

CNN + VAE

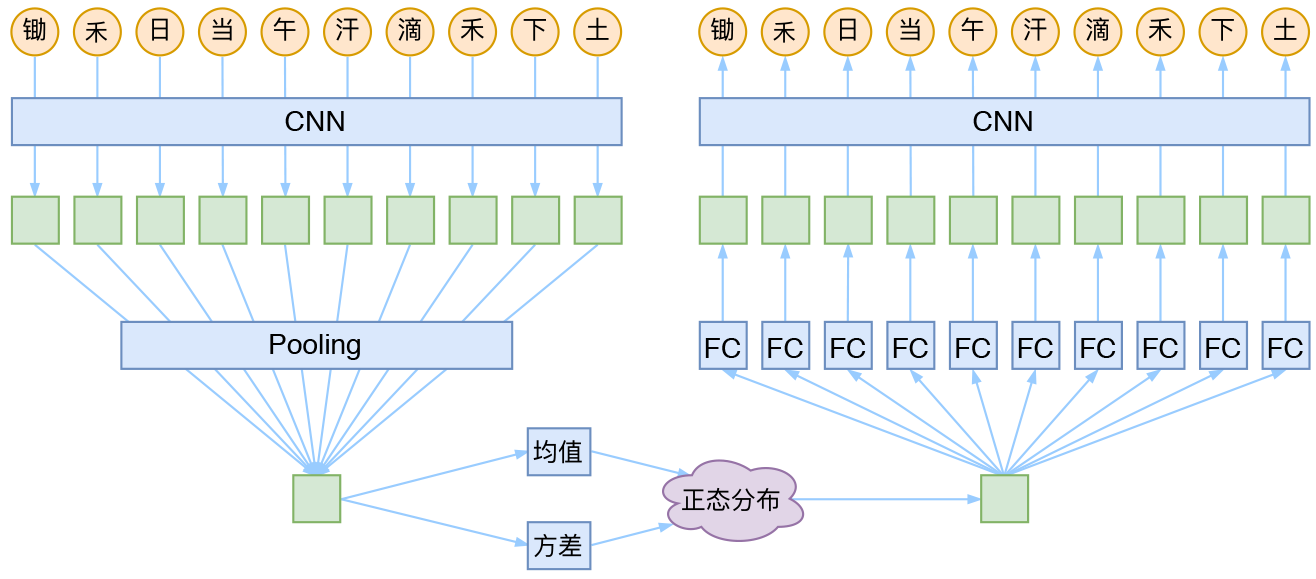
就本文的玩具而言，其实是一个比较简单的模型，主要是把一维CNN和VAE结合了起来。因为生成的诗长度是固定的，所以不管是encoder还是decoder，我都只是用了纯CNN来做。模型的结构图大概是：

cnn + vae 诗歌生成模型

点击阅读全文...

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。于是趁着最近看概率图模型的三分钟热度，我决定也争取把VAE搞懂。于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文《Auto-Encoding Variational Bayes》，最后我觉得我应该是想明白了。其实真正的VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来～于是写了这篇东西，希望通过下面的文字，能把VAE初步讲清楚。

分布变换

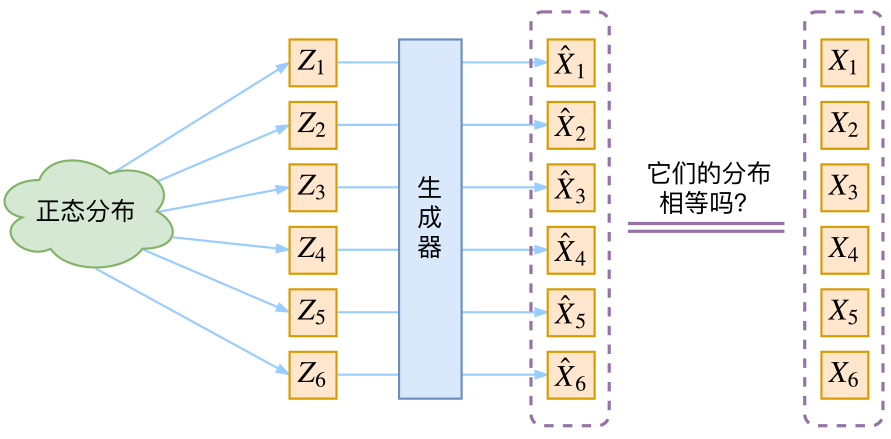
通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。更准确地讲，它们是假设了$Z$服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式

点击阅读全文...

最近在思考NLP的无监督学习和概率图相关的一些内容，于是重新把一些参数估计方法理了一遍。在深度学习中，参数估计是最基本的步骤之一了，也就是我们所说的模型训练过程。为了训练模型就得有个损失函数，而如果没有系统学习过概率论的读者，能想到的最自然的损失函数估计是平均平方误差，它也就是对应于我们所说的欧式距离。而理论上来讲，概率模型的最佳搭配应该是“交叉熵”函数，它来源于概率论中的最大似然函数。

最大似然

合理的存在

何为最大似然？哲学上有句话叫做“存在就是合理的”，最大似然的意思是“存在就是最合理的”。具体来说，如果事件$X$的概率分布为$p(X)$，如果一次观测中具体观测到的值分别为$X_1,X_2,\dots,X_n$，并假设它们是相互独立，那么
$$\mathcal{P} = \prod_{i=1}^n p(X_i)\tag{1}$$
是最大的。如果$p(X)$是一个带有参数$\theta$的概率分布式$p_{\theta}(X)$，那么我们应当想办法选择$\theta$，使得$\mathcal{L}$最大化，即
$$\theta = \mathop{\text{argmax}}_{\theta} \mathcal{P}(\theta) = \mathop{\text{argmax}}_{\theta}\prod_{i=1}^n p_{\theta}(X_i)\tag{2}$$

点击阅读全文...

源起

前几天写了博文《变分自编码器（一）：原来是这么一回事》，从一种比较通俗的观点来理解变分自编码器（VAE），在那篇文章的视角中，VAE跟普通的自编码器差别不大，无非是多加了噪声并对噪声做了约束。然而，当初我想要弄懂VAE的初衷，是想看看究竟贝叶斯学派的概率图模型究竟是如何与深度学习结合来发挥作用的，如果仅仅是得到一个通俗的理解，那显然是不够的。

所以我对VAE继续思考了几天，试图用更一般的、概率化的语言来把VAE说清楚。事实上，这种思考也能回答通俗理解中无法解答的问题，比如重构损失用MSE好还是交叉熵好、重构损失和KL损失应该怎么平衡，等等。

建议在阅读《变分自编码器（一）：原来是这么一回事》后对本文进行阅读，本文在内容上尽量不与前文重复。

准备

在进入对VAE的描述之前，我觉得有必要把一些概念性的内容讲一下。

点击阅读全文...

2019.08.20更新：开源了一个Keras版（https://kexue.fm/archives/6906）

早在年初的《Attention is All You Need》的介绍文章中就已经承诺过会分享CNN在NLP中的使用心得，然而一直不得其便。这几天终于下定决心来整理一下相关的内容了。

背景

事不宜迟，先来介绍一下模型的基本情况。

模型特点

本模型——我称之为DGCNN——是基于CNN和简单的Attention的模型，由于没有用到RNN结构，因此速度相当快，而且是专门为这种WebQA式的任务定制的，因此也相当轻量级。SQUAD排行榜前面的模型，如AoA、R-Net等，都用到了RNN，并且还伴有比较复杂的注意力交互机制，而这些东西在DGCNN中基本都没有出现。

这是一个在GTX1060上都可以几个小时训练完成的模型！

截止到2018.04.14的排行榜

DGCNN，全名为Dilate Gated Convolutional Neural Network，即“膨胀门卷积神经网络”，顾名思义，融合了两个比较新的卷积用法：膨胀卷积、门卷积，并增加了一些人工特征和trick，最终使得模型在轻、快的基础上达到最佳的效果。在本文撰写之时，本文要介绍的模型还位于榜首，得分（得分是准确率与F1的平均）为0.7583，而且是到目前为止唯一一个一直没有跌出前三名、并且获得周冠军次数最多的模型。

点击阅读全文...

话说我觉得我自己最近写文章都喜欢长篇大论了，而且扎堆地来～之前连续写了三篇关于Capsule的介绍，这次轮到VAE了，本文是VAE的第三篇探索，说不准还会有第四篇～不管怎么样，数量不重要，重要的是能把问题都想清楚。尤其是对于VAE这种新奇的建模思维来说，更加值得细细地抠。

这次我们要关心的一个问题是：VAE为什么能成？

估计看VAE的读者都会经历这么几个阶段。第一个阶段是刚读了VAE的介绍，然后云里雾里的，感觉像自编码器又不像自编码器的，反复啃了几遍文字并看了源码之后才知道大概是怎么回事；第二个阶段就是在第一个阶段的基础上，再去细读VAE的原理，诸如隐变量模型、KL散度、变分推断等等，细细看下去，发现虽然折腾来折腾去，最终居然都能看明白了。

这时候读者可能就进入第三个阶段了。在这个阶段中，我们会有诸多疑问，尤其是可行性的疑问：“为什么它这样反复折腾，最终出来模型是可行的？我也有很多想法呀，为什么我的想法就不行？”

前文之要

让我们再不厌其烦地回顾一下前面关于VAE的一些原理。

VAE希望通过隐变量分解来描述数据$X$的分布
$$p(x)=\int p(x|z)p(z)dz,\quad p(x,z) = p(x|z)p(z)\tag{1}$$

点击阅读全文...

笔者去年曾写过博文《果壳中的条件随机场(CRF In A Nutshell)》，以一种比较粗糙的方式介绍了一下条件随机场（CRF）模型。然而那篇文章显然有很多不足的地方，比如介绍不够清晰，也不够完整，还没有实现，在这里我们重提这个模型，将相关内容补充完成。

本文是对CRF基本原理的一个简明的介绍。当然，“简明”是相对而言中，要想真的弄清楚CRF，免不了要提及一些公式，如果只关心调用的读者，可以直接移到文末。

图示

按照之前的思路，我们依旧来对比一下普通的逐帧softmax和CRF的异同。

逐帧softmax

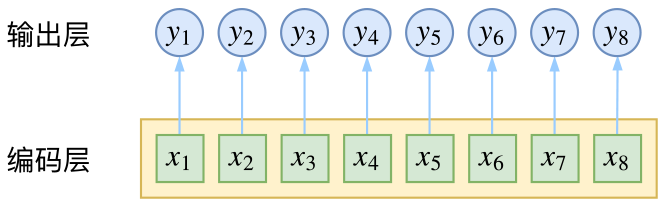
CRF主要用于序列标注问题，可以简单理解为是给序列中的每一帧都进行分类，既然是分类，很自然想到将这个序列用CNN或者RNN进行编码后，接一个全连接层用softmax激活，如下图所示

逐帧softmax并没有直接考虑输出的上下文关联

点击阅读全文...