科学空间|Scientific Spaces

这篇文章要带来一个“重磅”消息，如标题所示，居然连大名鼎鼎的深度学习词向量工具Word2Vec都只不过是个SVD！

当然，Word2Vec的超级忠实粉丝们，你们也不用太激动，这里只是说模型结构上是等价的，并非完全等价，Word2Vec还是有它的独特之处。只不过，经过我这样解释之后，估计很多问题就可以类似想通了。

词向量=one hot

让我们先来回顾一下去年的一篇文章《词向量与Embedding究竟是怎么回事？》，这篇文章主要说的是：所谓Embedding层，就是一个one hot的全连接层罢了（再次强调，这里说的完全等价，而不是“相当于”），而词向量，就是这个全连接层的参数；至于Word2Vec，就通过大大简化的语言模型来训练Embedding层，从而得到词向量（它的优化技巧有很多，但模型结构就只是这么简单）；词向量能够减少过拟合风险，是因为用Word2Vec之类的工具、通过大规模语料来无监督地预训练了这个Embedding层，而跟one hot还是Embedding还是词向量本身没啥关系。

有了这个观点后，马上可以解释我们以前的一个做法为什么可行了。在做情感分类问题时，如果有了词向量，想要得到句向量，最简单的一个方案就是直接对句子中的词语的词向量求和或者求平均，这约能达到85%的准确率。事实上这也是facebook出品的文本分类工具FastText的做法了（FastText还多引入了ngram特征，来缓解词序问题，但总的来说，依旧是把特征向量求平均来得到句向量）。为什么这么一个看上去毫不直观的、简单粗暴的方案也能达到这么不错的准确率？

点击阅读全文...

信息抽取

众所周知，百度知道上有大量的人提了大量的问题，并且得到大量的回复。然而，百度知道上的回复者貌似懒人居多，他们往往喜欢直接在网上复制粘贴一大片来作为回答内容，而且这些内容可能跟问题相关，也可能跟问题不相关，比如

https://zhidao.baidu.com/question/557785746.html

问：广州白云山海拨多高

答：广州白云山（Guangzhou Baiyun Mountain），是新 “羊城八景”之首、国家4A级景区和国家重点风景名胜区。它位于广州市的东北部，为南粤名山之一，自古就有“羊城第一秀”之称。山体相当宽阔，由30多座山峰组成，为广东最高峰九连山的支脉。面积20.98平方公里，主峰摩星岭高382米（注：最新测绘高度为372.6米——国家测绘局，2008年），峰峦重叠，溪涧纵横，登高可俯览全市，遥望珠江。每当雨后天晴或暮春时节，山间白云缭绕，蔚为奇观，白云山之名由此得来

点击阅读全文...

相似度的定义

当用Word2Vec得到词向量后，一般我们会用余弦相似度来比较两个词的相似程度，定义为
$$\cos (\boldsymbol{x}, \boldsymbol{y}) = \frac{\boldsymbol{x}\cdot\boldsymbol{y}}{|\boldsymbol{x}|\times|\boldsymbol{y}|}$$
有了这个相似度概念，我们既可以比较任意两个词之间的相似度，也可以找出跟给定词最相近的词语。这在gensim的Word2Vec中，由most_similar函数实现。

等等！我们很快给出了相似度的计算公式，可是我们居然还没有“定义”相似！连相似都没有定义，怎么就得到了评估相似度的数学公式了呢？

要注意，这不是一个可以随意忽略的问题。很多时候我们都不知道我们干的是什么，就直接去干了。好比上一篇文章说到提取关键词，相信很多人都未曾想过，什么是关键词，难道就仅仅说关键词就是很“关键”的词？而如果想到，关键词就是用来估计文章大概讲什么的，这样我们就得到一种很自然的关键词定义
$$keywords = \mathop{\text{argmax}}_{w\in s}p(s|w)$$
进而可以用各种方法对它建模。

回到本文的主题来，相似度怎么定义呢？答案是：看场景定义所需要的相似。

点击阅读全文...

前言

GAN，全称Generative Adversarial Nets，中文名是生成对抗式网络。对于GAN来说，最通俗的解释就是“伪造者-鉴别者”的解释，如艺术画的伪造者和鉴别者。一开始伪造者和鉴别者的水平都不高，但是鉴别者还是比较容易鉴别出伪造者伪造出来的艺术画。但随着伪造者对伪造技术的学习后，其伪造的艺术画会让鉴别者识别错误；或者随着鉴别者对鉴别技术的学习后，能够很简单的鉴别出伪造者伪造的艺术画。这是一个双方不断学习技术，以达到最高的伪造和鉴别水平的过程。 然而，稍微深入了解的读者就会发现，跟现实中的造假者不同，造假者会与时俱进地使用新材料新技术来造假，而GAN最神奇而又让人困惑的地方是它能够将随机噪声映射为我们所希望的正样本，有噪声就有正样本，这不是无本生意吗，多划算～

另一个情况是，自从WGAN提出以来，基本上GAN的主流研究都已经变成了WGAN上去了，但WGAN的形式事实上已经跟“伪造者-鉴别者”差得比较远了。而且WGAN虽然最后的形式并不复杂，但是推导过程却用到了诸多复杂的数学，使得我无心研读原始论文。这迫使我要找从一条简明直观的线索来理解GAN。幸好，经过一段时间的思考，有点收获。

点击阅读全文...

前言

从今年开始，CCL会议将计划同步举办评测活动。笔者这段时间在一创业公司实习，公司也报名参加这个评测，最后实现上就落在我这里，今年的评测任务是阅读理解，名曰《第一届“讯飞杯”中文机器阅读理解评测》。虽说是阅读理解，但事实上任务比较简单，是属于完形填空类型的，即一段材料中挖了一个空，从上下文中选一个词来填入这个空中。最后我们的模型是单系统排名第6，验证集准确率为73.55%，测试集准确率为75.77%，大家可以在这里观摩排行榜。（“广州火焰信息科技有限公司”就是文本的模型）

事实上，这个数据集和任务格式是哈工大去年提出的，所以这次的评测也是哈工大跟科大讯飞一起联合举办的。哈工大去年的论文《Consensus Attention-based Neural Networks for Chinese Reading Comprehension》就研究过另一个同样格式但不同内容的数据集，是用通用的阅读理解模型做的（通用的阅读理解是指给出材料和问题，从材料中找到问题的答案，完形填空可以认为是通用阅读理解的一个非常小的子集）。

虽然，在这次评测任务的介绍中，评测方总有意无意地引导我们将这个问题理解为阅读理解问题。但笔者觉得，阅读理解本身就难得多，这个就一完形填空，只要把它作为纯粹的完形填空题做就是了，所以本文仅仅是采用类似语言模型的做法来做。这种做法的好处是思路简明直观，计算量低（在笔者的GTX1060上可以跑到batch size为160），便于实验。

模型

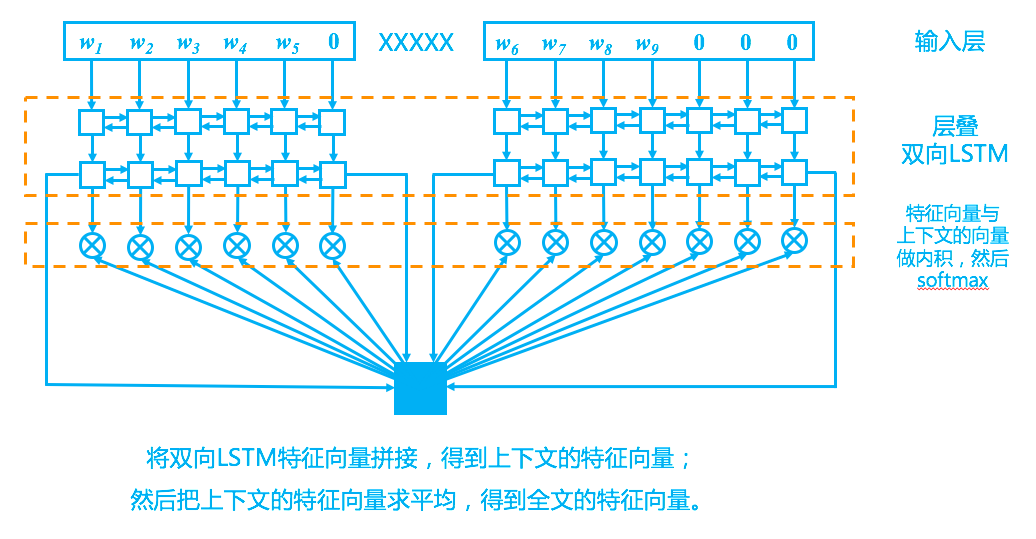
回到模型上，我们的模型其实比较简单，完全紧扣了“从上下文中选一个词来填空”这一思想，示意图如下。

完形填空模型

点击阅读全文...

Keras是一个搭积木式的深度学习框架，用它可以很方便且直观地搭建一些常见的深度学习模型。在tensorflow出来之前，Keras就已经几乎是当时最火的深度学习框架，以theano为后端，而如今Keras已经同时支持四种后端：theano、tensorflow、cntk、mxnet（前三种官方支持，mxnet还没整合到官方中），由此可见Keras的魅力。

Keras是很方便，然而这种方便不是没有代价的，最为人诟病之一的缺点就是灵活性较低，难以搭建一些复杂的模型。的确，Keras确实不是很适合搭建复杂的模型，但并非没有可能，而是搭建太复杂的模型所用的代码量，跟直接用tensorflow写也差不了多少。但不管怎么说，Keras其友好、方便的特性（比如那可爱的训练进度条），使得我们总有使用它的场景。这样，如何更灵活地定制Keras模型，就成为一个值得研究的课题了。这篇文章我们来关心自定义loss。

输入-输出设计

Keras的模型是函数式的，即有输入，也有输出，而loss即为预测值与真实值的某种误差函数。Keras本身也自带了很多loss函数，如mse、交叉熵等，直接调用即可。而要自定义loss，最自然的方法就是仿照Keras自带的loss进行改写。

点击阅读全文...

不管是打比赛、做实验还是搞工程，我们经常会遇到训练集与测试集分布不一致的情况。一般来说我们会从训练集中划分出来一个验证集，通过这个验证集来调整一些超参数（参考《训练集、验证集和测试集的意义》），比如控制模型的训练轮数以防止过拟合。然而，如果验证集本身跟测试集差别比较大，那么验证集上很好的模型也不代表在测试集上很好，因此如何让划分出来验证集跟测试集的分布差异更小一些，是一个值得研究的题目。

两种情况

首先，明确一下，本文所考虑的，是能给拿到测试集数据本身、但不知道测试集标签的场景。如果是那种提交模型封闭评测的场景，我们完全看不到测试集的，那就没什么办法了。为什么会出现测试集跟训练集分布不一致的现象呢？主要有两种情况。

点击阅读全文...

主方程（master equation）是对随机过程进行建模的重要方法，它代表着马尔科夫过程的微分形式，我们的专业主要工具之一就是主方程，说宏大一点，量子力学和统计力学等也不外乎是主方程的一个特例。

然而，笔者阅读了几个著作，比如《统计物理现代教程》，还有我导师的《生物系统的随机动力学》，我发现这些著作对于主方程的推导都很模糊，他们在着力解释结果的意义，但并不说明结果的思想来源，因此其过程难以让人信服。而知乎上有人提问《如何理解马尔科夫过程的主方程的推导过程？》但没有得到很好的答案，也表明了这个事实。

马尔可夫过程

主方程是用来描述马尔科夫过程的，而马尔科夫过程可以理解为运动的无记忆性，说通俗点，就是下一刻的概率分布，只跟当前时刻有关，跟历史状态无关。用概率公式写出来就是（这里只考虑连续型概率，因此这里的$p$是概率密度）：
$$\begin{equation}\label{eq:maerkefu}p(x,\tau)=\int p(x,\tau|y,t) p(y,t) dy\end{equation}$$
这里的积分区域是全空间。这里的$p(x,\tau|y,t)$称为跃迁概率，即已经确定了$t$时刻来到了$y$位置后、在$\tau$时刻达到$x$的概率密度，这个式子的物理意义是很明显的，就不多做解释了。

点击阅读全文...