科学空间|Scientific Spaces

————怀念我曾经参加过的小学数学竞赛。

从一道小学竞赛题谈起

笔者小学五年级时参加了第一次数学竞赛，叫“育苗杯”，大多数题目都记不清楚了，唯一记得很清楚的是如下这道题目（不完全相同，意思类似）：

假设汽水一块钱一瓶，而且4个空瓶子可以换一瓶汽水喝。如果我有30块钱，我最多可以喝到多少瓶汽水？

来瓶汽水吧

当然，这道题并不困难，30块钱能买30瓶汽水，然后留下30个空瓶子，这30个空瓶子可以换来7瓶汽水，剩下2个空瓶子；喝完汽水后，剩下9个空瓶子，可以换来2瓶汽水，剩下1个空瓶子；喝完汽水后，剩下3个空瓶子。算算看，这时候我们已经喝了30+7+2=39瓶汽水了。（不考虑撑着啊，也可以分给别人喝^_^）整个过程如下表：
$$\begin{array}{c|cccc}
\hline
\text{空瓶子数} & 30 & 2+7 & 1+2 & ? \\
\hline
\text{已喝汽水数} & 30 & 7 & 2 & ? \\
\hline \end{array}$$

点击阅读全文...

记得很早之前就想尝试一下拍星空，无奈一直都没有设备。以前只知道单反可以拍星空，因此，一直以来的想法就是有钱了就去买台单反。因为各种原因一拖再拖，最后慢慢觉得，对于我这种三分钟热度的人来说，单反的意义还真的不是很大。

这两年，在小米的鼓吹下，小蚁运动相机在国内算是慢慢掀起了一股运动相机潮。这种相机的特点是小巧、灵活，价格也不贵（相比单反）。灵活不仅仅是说它便于携带，而且还是功能上的灵活，比如一代小蚁还支持编程拍摄！（写程序控制快门、ISO、拍摄间隔，并实现定时拍摄等）这样当然很快就吸引了我，在小蚁2代众筹之时，我也咬咬牙，入了一台。

前两天回到家，刚好晴夜，马上就试了一下拍星空的效果。下面是在我家楼顶拍的，用ISO400曝光30秒的效果：

家乡的星空

点击阅读全文...

最近一直在考虑一些自然语言处理问题和一些非线性分析问题，无暇总结发文，在此表示抱歉。本文要说的是对于一阶非线性差分方程（当然高阶也可以类似地做）的一种摄动格式，理论上来说，本方法可以得到任意一阶非线性差分方程的显式渐近解。

非线性差分方程

对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说，差分方程很少有解析解，因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候，我们首先会考虑将差分替换为求导，得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
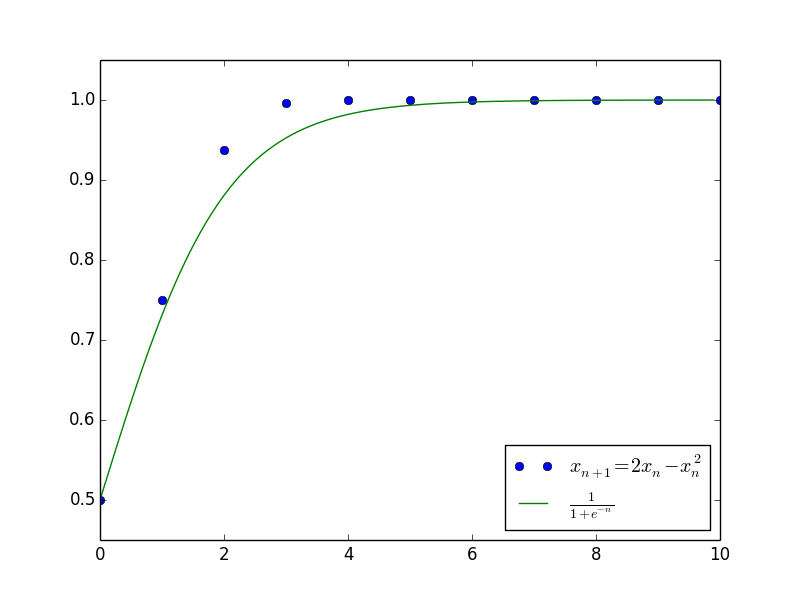
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因，除了微分方程有比较简单的显式解之外，另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质，如渐近性。例如，考虑离散的阻滞增长模型：
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为（差分替换为求导）：
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势，并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$（即$x_0=\frac{1}{2}$）时，微分方程的解与差分方程的解的值比较。

差分方程的摄动法1

现在的问题是，既然微分方程的解可以作为一个形态良好的近似解了，那么是否可以在微分方程的解的基础上，进一步加入修正项提高精度？

点击阅读全文...

Python数据分析与挖掘实战

暑假的时候，应泰迪公司之约，我为他们的书《MATLAB数据挖掘与挖掘实战》编写了姊妹版：《Python数据挖掘与挖掘实战》（还有一个姊妹版是R语言的），主要的工作内容就是编写Python的介绍，以及把书上的MATLAB代码翻译为Python版本的。我欣然接受了，一来可以兼职赚点零花钱，二来可以系统地训练一下自身的Python编程，再则，还可以体验一次MATLAB、R、Python的大PK。现在书本已经正式发行，亚马逊、当当、京东、淘宝都可以找到，我也很荣幸被列为作者之一，于是这便算是我出版的第一本书了。

点击阅读全文...

众所周知，校园网最宝贵的资源应该有两样：一是IPv6，IPv6是访问Google等网站的最理想途径，当然IPv6并非所有高校都有；二是论文库，一般高校都会买了一部分论文库（知网、万方等）的下载权，供校园用户使用。如果说访问Google还有VPN等诸多方式的话，那么对于校外用户来说访问知网等资源就显得格外宝贵了，一般只是叫校内用户下载，或者就只能付费了（那个贵呀！）。

站长还是学生，在学校同时享用着IPv6和论文库资源，确实很爽。自从用上Openwrt的路由之后，一直想着怎么把校园网资源共享出去。曾经考虑过搭建PPTP VPN，但是感觉略有复杂（当然，跟其他VPN相比，搭建PPTP VPN算是非常简单的了，可是我还是不怎么喜欢。），而且当时还没解决内网穿透的问题。最近借助ssh反向代理的方式实现了内网穿透，继而认识到，通过ssh动态端口转发，居然还可以搭建代理，并且实现远程访问内网（校园网）资源，而且几乎不用在路由器本身上面做任何配置。不得不说，ssh真是一个极其强大的东西呀。

添加普通帐号

既然要共享，就没理由把root账户都分享出去了，因此，第一步要实现的是在Openwrt上添加一个代理账号，而且为了安全和保密，这个账号不允许真的登陆服务器进行操作，而只允许进行端口转发。

点击阅读全文...

记得科学空间刚开始的时候，没有什么原创的内容，有一段时间在翻译APOD的图片，后来渐渐地专注原创，就没有翻译了。这次再来分享一张图片，是兴隆山上的双子座流星雨，是国内爱好者Steed Yu拍摄的，被APOD收录。

兴隆山的双子座流星雨（来源：http://apod.nasa.gov/apod/ap151223.html）

点击阅读全文...

最近在算路径积分的时候，频繁地遇到了以下两种无穷级数：
$$\sum_n \frac{1}{n^2\pm\omega^2}\quad \text{和} \quad \prod_n \left(1\pm\frac{\omega^2}{n^2}\right)$$
当然，直接用Mathematica可以很干脆地算出结果来，但是我还是想知道为什么，至少大概地知道。

伯努利级数

当$\omega=0$的时候，第一个级数变为著名的伯努利级数
$$\sum_n \frac{1}{n^2}=1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\dots$$
既然跟伯努利级数有关，那么很自然想到，从伯努利级数的求和入手。

点击阅读全文...

问题来源

笔者经常学习的数学研发论坛曾有一帖讨论下述非线性差分方程的渐近求解：
$$a_{n+1}=a_n+\frac{1}{a_n^2},\, a_1=1$$
原帖子在这里，从这帖子中我获益良多，学习到了很多新技巧。主要思路是通过将两边立方，然后设$x_n=a_n^3$，变为等价的递推问题：
$$x_{n+1}=x_n+3+\frac{3}{x_n}+\frac{1}{x_n^2},\,x_1=1$$
然后可以通过巧妙的技巧得到渐近展开式：
$$x_n = 3n+\ln n+a+\frac{\frac{1}{3}(\ln n+a)-\frac{5}{18}}{n}+\dots$$
具体过程就不提了，读者可以自行到上述帖子学习。

然而，这种形式的解虽然精妙，但存在一些笔者不是很满意的地方：

1、解是渐近的级数，这就意味着实际上收敛半径为0；
2、是$n^{-k}$形式的解，对于较小的$n$难以计算，这都使得高精度计算变得比较困难；
3、当然，题目本来的目的是渐近计算，但是渐近分析似乎又没有必要展开那么多项；
4、里边带有了一个本来就比较难计算的极限值$a$；
5、求解过程似乎稍欠直观。

当然，上面这些缺点，有些是鸡蛋里挑骨头的。不过，也正是这些缺点，促使我寻找更好的形式的解，最终导致了这篇文章。

点击阅读全文...