15
Feb
能量视角下的GAN模型（二）：GAN＝“分析”＋“采样”
By 苏剑林 | 2019-02-15 | 132416位读者 | 引用在这个系列中，我们尝试从能量的视角理解GAN。我们会发现这个视角如此美妙和直观，甚至让人拍案叫绝。
上一篇文章里，我们给出了一个直白而用力的能量图景，这个图景可以让我们轻松理解GAN的很多内容，换句话说，通俗的解释已经能让我们完成大部分的理解了，并且把最终的结论都已经写了出来。在这篇文章中，我们继续从能量的视角理解GAN，这一次，我们争取把前面简单直白的描述，用相对严密的数学语言推导一遍。
跟第一篇文章一样，对于笔者来说，这个推导过程依然直接受启发于Bengio团队的新作《Maximum Entropy Generators for Energy-Based Models》。
原作者的开源实现：https://github.com/ritheshkumar95/energy_based_generative_models
本文的大致内容如下：
1、推导了能量分布下的正负相对抗的更新公式；
2、比较了理论分析与实验采样的区别，而将两者结合便得到了GAN框架；
3、导出了生成器的补充loss，理论上可以防止mode collapse；
4、简单提及了基于能量函数的MCMC采样。
7
Nov
WGAN-div：一个默默无闻的WGAN填坑者
By 苏剑林 | 2018-11-07 | 157745位读者 | 引用今天我们来谈一下Wasserstein散度，简称“W散度”。注意，这跟Wasserstein距离（Wasserstein distance，简称“W距离”，又叫Wasserstein度量、Wasserstein metric）是不同的两个东西。
本文源于论文《Wasserstein Divergence for GANs》，论文中提出了称为WGAN-div的GAN训练方案。这是一篇我很是欣赏却默默无闻的paper，我只是找文献时偶然碰到了它。不管英文还是中文界，它似乎都没有流行起来，但是我感觉它是一个相当漂亮的结果。
WGAN-div的部分样本（2w iter）
如果读者需要入门一下WGAN的相关知识，不妨请阅读拙作《互怼的艺术：从零直达WGAN-GP》。
WGAN
我们知道原始的GAN（SGAN）会有可能存在梯度消失的问题，因此WGAN横空出世了。
W距离
WGAN引入了最优传输里边的W距离来度量两个分布的距离：
\begin{equation}W_c[\tilde{p}(x), q(x)] = \inf_{\gamma\in \Pi(\tilde{p}(x), q(x))} \mathbb{E}_{(x,y)\sim \gamma}[c(x,y)] \end{equation}
这里的$\tilde{p}(x)$是真实样本的分布，$q(x)$是伪造分布，$c(x,y)$是传输成本，论文中用的是$c(x,y)=\Vert x-y\Vert$；而$\gamma\in \Pi(\tilde{p}(x), q(x))$的意思是说：$\gamma$是任意关于$x, y$的二元分布，其边缘分布则为$\tilde{p}(x)$和$q(y)$。直观来看，$\gamma$描述了一个运输方案，而$c(x,y)$则是运输成本，$W_c[\tilde{p}(x), q(x)]$就是说要找到成本最低的那个运输方案所对应的成本作为分布度量。
8
Jan
从动力学角度看优化算法（三）：一个更整体的视角
By 苏剑林 | 2019-01-08 | 59649位读者 | 引用
18
Feb
恒等式 det(exp(A)) = exp(Tr(A)) 赏析
By 苏剑林 | 2019-02-18 | 67431位读者 | 引用本文的主题是一个有趣的矩阵行列式的恒等式
\begin{equation}\det(\exp(\boldsymbol{A})) = \exp(\text{Tr}(\boldsymbol{A}))\label{eq:main}\end{equation}
这个恒等式在挺多数学和物理的计算中都出现过，笔者都在不同的文献中看到过好几次了。
注意左端是矩阵的指数，然后求行列式，这两步都是计算量非常大的运算；右端仅仅是矩阵的迹（一个标量），然后再做标量的指数。两边的计算量差了不知道多少倍，然而它们居然是相等的！这不得不说是一个神奇的事实。
所以，本文就来好好欣赏一个这个恒等式。
21
Mar
细水长flow之可逆ResNet：极致的暴力美学
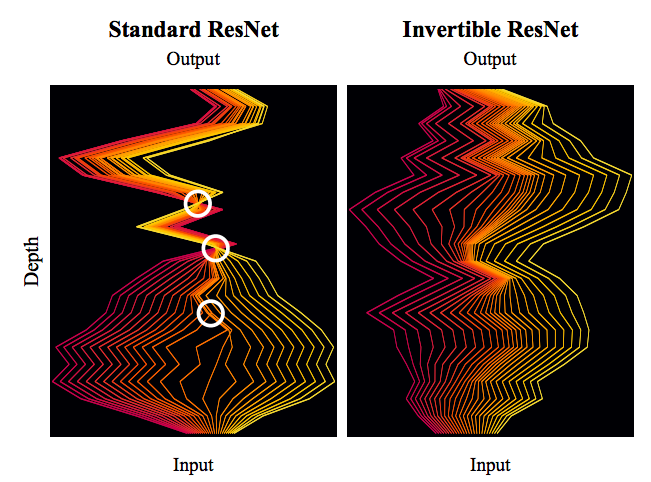
By 苏剑林 | 2019-03-21 | 114237位读者 | 引用今天我们来介绍一个非常“暴力”的模型：可逆ResNet。
为什么一个模型可以可以用“暴力”来形容呢？当然是因为它确实非常暴力：它综合了很多数学技巧，活生生地（在一定约束下）把常规的ResNet模型搞成了可逆的！
标准ResNet与可逆ResNet对比图。可逆ResNet允许信息无损可逆流动，而标准ResNet在某处则存在“坍缩”现象。
模型出自《Invertible Residual Networks》，之前在机器之心也报导过。在这篇文章中，我们来简单欣赏一下它的原理和内容。
可逆模型的点滴
为什么要研究可逆ResNet模型？它有什么好处？以前没有人研究过吗？
可逆的好处
可逆意味着什么？
意味着它是信息无损的，意味着它或许可以用来做更好的分类网络，意味着可以直接用最大似然来做生成模型，而且得益于ResNet强大的能力，意味着它可能有着比之前的Glow模型更好的表现～总而言之，如果一个模型是可逆的，可逆的成本不高而且拟合能力强，那么它就有很广的用途（分类、密度估计和生成任务，等等）。
3
May
从动力学角度看优化算法（四）：GAN的第三个阶段
By 苏剑林 | 2019-05-03 | 97209位读者 | 引用在对GAN的学习和思考过程中，我发现我不仅学习到了一种有效的生成模型，而且它全面地促进了我对各种模型各方面的理解，比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”，而是具有深刻意义的概率模型和推断方法。
作为事后的总结，我觉得对GAN的理解可以粗糙地分为三个阶段：
1、样本阶段：在这个阶段中，我们了解了GAN的“鉴别者-造假者”诠释，懂得从这个原理出发来写出基本的GAN公式（如原始GAN、LSGAN），比如判别器和生成器的loss，并且完成简单GAN的训练；同时，我们知道GAN有能力让图片更“真”，利用这个特性可以把GAN嵌入到一些综合模型中。
2、分布阶段：在这个阶段中，我们会从概率分布及其散度的视角来分析GAN，典型的例子是WGAN和f-GAN，同时能基本理解GAN的训练困难问题，比如梯度消失和mode collapse等，甚至能基本地了解变分推断，懂得自己写出一些概率散度，继而构造一些新的GAN形式。
3、动力学阶段：在这个阶段中，我们开始结合优化器来分析GAN的收敛过程，试图了解GAN是否能真的达到理论的均衡点，进而理解GAN的loss和正则项等因素如何影响的收敛过程，由此可以针对性地提出一些训练策略，引导GAN模型到达理论均衡点，从而提高GAN的效果。
10
May
能量视角下的GAN模型（三）：生成模型=能量模型
By 苏剑林 | 2019-05-10 | 54663位读者 | 引用
本文的模型在ImageNet(128x128)上的条件生成效果
今天要介绍的结果还是跟能量模型相关，来自论文《Implicit Generation and Generalization in Energy-Based Models》。当然，它已经跟GAN没有什么关系了，但是跟本系列第二篇所介绍的能量模型关系较大，所以还是把它放到这个系列好了。
我当初留意到这篇论文，是因为机器之心的报导《MIT本科学神重启基于能量的生成模型，新框架堪比GAN》，但是说实在的，这篇文章没什么意思，说句不中听的，就是炒冷饭系列，媒体的标题也算中肯，是“重启”。这篇文章就是指出能量模型实际上就是某个特定的Langevin方程的静态解，然后就用这个Langevin方程来实现采样，有了采样过程也就可以完成能量模型的训练，这些理论都是现成的，所以这个过程我在学习随机微分方程的时候都想过，我相信很多人也都想过。因此，我觉得作者的贡献就是把这个直白的想法通过一系列炼丹技巧实现了。
但不管怎样，能训练出来也是一件很不错的事情，另外对于之前没了解过相关内容的读者来说，这确实也算是一个不错的能量模型案例，所以我论文的整体思路整理一下，让读者能够更全面地理解能量模型。
6
Jul
最近评论