细水长flow之可逆ResNet:极致的暴力美学
By 苏剑林 | 2019-03-21 | 165346位读者 |今天我们来介绍一个非常“暴力”的模型:可逆ResNet。
为什么一个模型可以可以用“暴力”来形容呢?当然是因为它确实非常暴力:它综合了很多数学技巧,活生生地(在一定约束下)把常规的ResNet模型搞成了可逆的!
模型出自《Invertible Residual Networks》,之前在机器之心也报导过。在这篇文章中,我们来简单欣赏一下它的原理和内容。
可逆模型的点滴 #
为什么要研究可逆ResNet模型?它有什么好处?以前没有人研究过吗?
可逆的好处 #
可逆意味着什么?
意味着它是信息无损的,意味着它或许可以用来做更好的分类网络,意味着可以直接用最大似然来做生成模型,而且得益于ResNet强大的能力,意味着它可能有着比之前的Glow模型更好的表现~总而言之,如果一个模型是可逆的,可逆的成本不高而且拟合能力强,那么它就有很广的用途(分类、密度估计和生成任务,等等)。
而本文要介绍的可逆ResNet基本上满足这几点要求,它可逆起来比较简单,而且基本上不改变ResNet的拟合能力。因此,我认为它称得上是“美”的模型。
旧模型的局限 #
可逆模型的研究由来已久,它们被称为“流模型(flow-based model)”,代表模型有NICE、RealNVP和Glow,笔者曾撰文介绍过它们,另外还有一些自回归流模型。除了用来做生成模型,用可逆模型来做分类任务的也有研究,代表作是RevNet和i-RevNet。
这些流模型的设计思路基本上都是一样的:通过比较巧妙的设计,使得模型每一层的逆变换比较简单,而且雅可比矩阵是一个三角阵,从而雅可比行列式很容易计算。这样的模型在理论上很优雅漂亮,但是有一个很严重的问题:由于必须保证逆变换简单和雅可比行列式容易计算,那么每一层的非线性变换能力都很弱。事实上像Glow这样的模型,每一层只有一半的变量被变换,所以为了保证充分的拟合能力,模型就必须堆得非常深(比如256的人脸生成,Glow模型堆了大概600个卷积层,两亿参数量),计算量非常大。
硬“杠”残差模型 #
而这一次的可逆ResNet跟以往的流模型不一样,它就是在普通的ResNet结构基础上加了一些约束,就使得模型成为可逆的,实际上依然保留了ResNet的基本结构和大部分的拟合能力。这样一来,以往我们在ResNet的设计经验基本上还可以用,而且模型不再需要像Glow那样拼命堆卷积了。
当然,这样做是有代价的,因为没有特别的设计,所以我们需要比较暴力的方法才能获得它的逆函数和雅可比行列式。所以,这次的可逆ResNet,很美,但也很暴力,称得上是“极致的暴力美学”。
可逆“三要素” #
ResNet模型的基本模块就是
\begin{equation}y = x + g(x)\triangleq F(x)\label{eq:resnet}\end{equation}
也就是说本来想用一个神经网络拟合$y$的,现在变成了用神经网络拟合$y-x$了,其中$x,y$都是向量(张量)。这样做的好处是梯度不容易消失,能训练深层网络,让信息多通道传输,等等~可逆的意思就是$x+g(x)$是一个一一映射,也就是说每个$x$只有一个$y$与之对应,反过来也是,换言之我们理论中可以从中解出反函数$x=h(y)$来。
背景就不多说了,但是要说明一点,我们在分类问题中用的广义上的ResNet,是允许通过$1\times 1$卷积改变维度的,但这里的ResNet指的是不改变维度的ResNet,也就是说$x,y$的大小保持一样。
对于一个号称“可逆”的模型,必须要回答三个问题:
1、什么时候可逆?
2、逆函数是什么?
3、雅可比行列式怎么算?
从难度上来看,这三个问题是层层递进的。当然,如果你只关心做分类问题,那么事实上保证第一点就行了;如果你关心重构图片,那么就需要第二点;如果你还想像Glow那样用最大似然来训练生成模型,那么就需要第三点。
下面按照原论文的思路,逐一解决这三个问题(三道“硬菜”),来一场暴力盛宴。
什么时候可逆? #
第一道硬菜是三道硬菜中相对容易啃的,当然只是“相对”,事实上也都用到了泛函分析的一些基础知识了。(客官,先别跑呀~)
因为$\eqref{eq:resnet}$是ResNet的基本模块,所以我们只需要保证每个模块都可逆就行了。而$\eqref{eq:resnet}$可逆的一个充分条件是:
\begin{equation}\text{Lip}(g) < 1\end{equation}
其中
\begin{equation}\text{Lip}(g) \triangleq \max_{x_1\neq x_2}\frac{\Vert g(x_1) - g(x_2)\Vert_2}{\Vert x_1 - x_2\Vert_2}\end{equation}
是函数$g$的Lipschitz范数。也就是说,$g$的Lipschitz范数小于1,就能保证$\eqref{eq:resnet}$可逆了。
那什么时候$g$的Lipschitz范数才会小于1呢?因为$g$是神经网络,卷积和全连接都无妨,神经网络是由矩阵运算和激活函数组合而成的,即代表结构是
\begin{equation}Activation(Wx+b)\end{equation}
那么由链式法则,“$g$的Lipschitz范数小于1”的一个充分条件是“$Activation$的Lipschitz范数不超过1”且“$Wx+b$的Lipschitz范数小于1”。而$Activation$只是个标量函数,“Lipschitz范数不超过1”意味着导数不超过1就行了,目前我们常用的激活函数(sigmoid、tanh、relu、elu、swish等)都满足,所以这一点不用管它;而“$Wx+b$的Lipschitz范数小于1”,意味着矩阵$W$的Lipschitz范数小于1。
矩阵$W$的Lipschitz范数其实也就是“谱范数”,记为$\text{Lip}(W)$或$\Vert W\Vert_2$都行。那啥时候出现过矩阵的谱范数?在《深度学习中的Lipschitz约束:泛化与生成模型》一文中我们讨论Lipschitz约束的时候就出现过,两者结合起来,结论就是:
对模型$g$的所有核权重$W$做谱归一化,然后乘上一个大于0小于1的系数$c$(即$W\leftarrow c W / \Vert W\Vert_2$),就可以使得$x+g(x)$可逆了。
逆函数是什么? #
为什么这样就可逆了?证明过程可以直接回答第二个问题,也就是说,我们直接把逆函数求出来,然后就知道什么条件下可逆了。
假如$y=x+g(x)$是可逆的,那么我们要想办法求出逆函数$x=h(y)$,这其实就是解一个非线性方程组。简单起见,我们考虑迭代
\begin{equation}x_{n+1}=y - g(x_n)\label{eq:nidiedai}\end{equation}
显然,迭代序列$\{x_n\}$是跟$y$有关的,而一旦$\{x_n\}$收敛到某个固定的函数
\begin{equation}\lim_{n\to\infty} x_n(y) = \hat{h}(y)\end{equation}
那么我们就有$\hat{h}(y)=y-g\left(\hat{h}(y)\right)$,这意味着$\hat{h}(y)$就是我们希望求的$x=h(y)$。
换句话说,如果迭代$\eqref{eq:nidiedai}$收敛,那么收敛的结果就是$x+g(x)$的逆函数。所以我们只需要搞清楚$\eqref{eq:nidiedai}$什么时候收敛。这时候前面的条件$\text{Lip}(g) < 1$就能用上了,我们有
\begin{equation}\forall x_1,x_2,\quad\Vert g(x_1) - g(x_2)\Vert_2\leq \text{Lip}(g)\Vert x_1 - x_2\Vert_2\end{equation}
所以
\begin{equation}\begin{aligned}\Vert x_{n+1} - x_{n}\Vert_2&=\Vert g(x_{n}) - g(x_{n-1})\Vert_2\\
&\leq \text{Lip}(g)\Vert x_{n} - x_{n-1}\Vert_2\\
& = \text{Lip}(g)\Vert g(x_{n-1}) - g(x_{n-2})\Vert_2\\
&\leq \text{Lip}(g)^2\Vert x_{n-1} - x_{n-2}\Vert_2\\
&\dots\\
&\leq \text{Lip}(g)^n\Vert x_{1} - x_{0}\Vert_2\\
\end{aligned}\end{equation}
可以看到,$\Vert x_{n+1} - x_{n}\Vert_2\to 0$的充分条件是$\text{Lip}(g) < 1$。
附:单纯指出$\Vert x_{n+1} - x_{n}\Vert_2\to 0$并不能说明序列$\{x_n\}$收敛,比如$\{\ln n\}$这个序列也满足这个条件,但发散。所以,为了证明$\text{Lip}(g) < 1$时$\{x_n\}$收敛,我们还需要多做一些工作。不过这是比较数学的部分了,考虑到部分读者可能不感兴趣,因此作为附注。
对于任意正整数$k$,我们继续考虑$\Vert x_{n+k} - x_{n}\Vert_2$:
\begin{equation}\begin{aligned}\Vert x_{n+k} - x_{n}\Vert_2&\leq\Vert x_{n+k} - x_{n+k-1}\Vert_2+\dots+\Vert x_{n+2} - x_{n+1}\Vert_2+\Vert x_{n+1} - x_{n}\Vert_2\\
&\leq \left(\text{Lip}(g)^{n+k-1}+\dots+\text{Lip}(g)^{n+1}+\text{Lip}(g)^{n}\right)\Vert x_{1} - x_{0}\Vert_2\\
& = \frac{1 - \text{Lip}(g)^k}{1 - \text{Lip}(g)}\cdot\text{Lip}(g)^{n}\Vert x_{1} - x_{0}\Vert_2\\
& \leq \frac{\text{Lip}(g)^n}{1 - \text{Lip}(g)}\Vert x_{1} - x_{0}\Vert_2
\end{aligned}\label{eq:cauchy}\end{equation}
可以看到我们得到了$\Vert x_{n+k} - x_{n}\Vert_2$的一个上界,它只与$n$有关,且可以任意小。也就是说,对于任意$\varepsilon > 0$,我们可以找到一个$n$,使得对于任意的正整数$k$都有$\Vert x_{n+k} - x_{n}\Vert_2 < \varepsilon$。这样的数列我们称为Cauchy列,它是必然收敛的。至此,我们终于证明了$\{x_n\}$的收敛性。顺便一提的是,在$\eqref{eq:cauchy}$中,取$k\to\infty$,我们得到:
\begin{equation}\left\Vert x^* - x_{n}\right\Vert_2 \leq \frac{\text{Lip}(g)^n}{1 - \text{Lip}(g)}\Vert x_{1} - x_{0}\Vert_2\end{equation}
也就是说,这个迭代算法的收敛速度跟正比于$\text{Lip}(g)^n$,那么自然是$\text{Lip}(g)$越小收敛越快,但是$\text{Lip}(g)$越小模型的拟合能力越弱,原论文中它的范围是0.5~0.9。说宏大一点,其实这就是泛函分析中的“巴拿赫不动点定理”,又称“压缩映射定理”(因为$\text{Lip}(g)$小于1,所以$g$被称为一个压缩映射。)。
这样一来,我们已经回答了为什么$\text{Lip}(g) < 1$就有$x+g(x)$可逆了,同时已经给出了求逆函数的方法——就是通过$\eqref{eq:nidiedai}$迭代到足够的精度:
当做好归一化操作使得$x+g(x)$可逆后,它的逆函数为$x_{n+1}=y - g(x_n)$的不动点。数值计算时,只需要迭代一定步数,使得满足精度要求即可。
终于,我们啃下了第二道硬菜。
雅可比行列式怎么算? #
下面来到三个问题中最“硬核”的一个问题:雅可比行列式怎么算?为了解决它,作者综合了数学分析、矩阵论、概率论、统计采样等多方面数学工具,堪称“暴力之最”、“硬菜之最”。
首先,为什么要算雅可比行列式?前面已经说了,只有做生成模型时才有这个必要,具体细节请参考本站最早的对流模型的介绍《细水长flow之NICE:流模型的基本概念与实现》。接着,我们知道雅可比行列式就是雅可比矩阵的行列式,所以要把雅可比矩阵算出来:
\begin{equation}J_F\triangleq \frac{\partial}{\partial x}(x+g(x))= I + \frac{\partial g}{\partial x}\triangleq I + J_g\end{equation}
再次提醒,虽然我偷懒没有加粗,但这里的$g$输出是一个向量,$x$也是一个向量,$\partial g / \partial x$实际上就是输入和输出两两配对求偏导数,结果是一个矩阵(雅可比矩阵)。
然后,雅可比行列式就是$\det(J_F)=\det (I+J_g)$,但事实上,在做生成模型的时候,我们真正要算的,是“雅可比行列式的绝对值的对数”,即
\begin{equation}\ln |\det(J_F)| = \ln |\det(I + J_g)|\equiv \ln \det(I + J_g)\end{equation}
最后一个恒等号,是因为$\det(I + J_g)$一定是正数,所以可以去掉绝对值。这是可以证明的,但只是细节部分,我们就不纠结了,读者自行去看作者提供的参考文献吧。
然后呢?直接按定义来计算雅可比行列式?不行,因为这样子计算量实在是太大了,而且反向传播的时候,还要算行列式的导数,那就更复杂了。作者们想出了繁琐但有效的解决方法,利用恒等式(参考《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》):
\begin{equation}\ln\det(\boldsymbol{B}) = \text{Tr}(\ln (\boldsymbol{B}))\end{equation}
我们得到
\begin{equation}\ln\det(I + J_g) = \text{Tr}(\ln (I+J_g))\end{equation}
如果能求出$\ln (I+J_g)$来,然后求迹(trace,对角线元素之和)就行了。怎么求$\ln (I+J_g)$呢?还是参考《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》,暴力展开:
\begin{equation}\ln (I + J_g) = \sum_{n=1}^{\infty}(-1)^{n-1}\frac{J_g^n}{n}\label{eq:duishujishu}\end{equation}
注意这个级数收敛的条件是$\Vert J_g\Vert_2 < 1$,这正好意味着$\text{Lip}(g) < 1$,而这正是可逆ResNet的约束,前后完全自洽。
现在$\ln (I + J_g)$变成了一个无穷级数,如果截断$n$项,那么误差也正比于$\text{Lip}(g)^n$,所以我们要看$\text{Lip}(g)$来决定截断的数目。于是我们可以写出
\begin{equation}\text{Tr}(\ln (I + J_g)) = \sum_{n=1}^{N}(-1)^{n-1}\frac{\text{Tr}(J_g^n)}{n}+\mathcal{O}\left(\text{Lip}(g)^N\right)\label{eq:det2tr}\end{equation}
问题解决了吗?上式需要我们去计算$J_g^n$,注意$J_g$是一个矩阵,我们要算矩阵的$n$次方(想想算两个矩阵乘法的工作量)。于是作者们想:
既然分析的工具用完了,那我们就上概率统计吧。
假设$p(u)$是一个多元概率分布,其均值为0、协方差为单位矩阵(显然标准正态分布符合要求),那么对于任意矩阵$A$,我们有
\begin{equation}\text{Tr}(A)=\mathbb{E}_{u\sim p(u)}\big[u^{\top}Au\big]\end{equation}
利用“均值为0、协方差为单位矩阵”这个性质,直接按定义就可以证明上式了,并不困难。然后,作者提出了一个显得“既无赖又合理”的方法:对于每次迭代,我只从$p(u)$中随机选一个向量$u$出来,然后认为$u^{\top}Au$就是$\text{Tr}(A)$,即
\begin{equation}\text{Tr}(\ln (I + J_g)) \approx \sum_{n=1}^{N}(-1)^{n-1}\frac{u^{\top} J_g^n u}{n},\quad u\sim p(u)\label{eq:tr-caiyang}\end{equation}
读者可能就有意见了,不是要对所有向量求平均吗?只随机挑一个就行了?其实还真的是可以了,理由如下:
1、我们优化都是基于随机梯度下降的,本来就带有误差,而只随机挑两个也有误差,而每步迭代都重新挑不同的$u_1,u_2$,在一定程度上就能抵消误差;
2、更重要的原因是,我们要算雅可比行列式的对数,只是用它来做一个额外的loss,来保证模型不会坍缩,简单来讲,可以将它看称一个正则项,而既然是一个正则项,有点误差也无妨。
所以,$\text{Tr}(J_g^n)$的计算就被作者用这么粗暴(又有效)的方案解决了。注意到
\begin{equation}u^{\top} J_g^n u=u^{\top} J_g(\dots(J_g(J_g u)))\end{equation}
所以不需要把$J_g^n$算出来,而是每步只需要算一个矩阵与一个向量的乘法,并且每步计算可以重复利用,因此计算量是大大减少的。
所以,最终可以总结为:
将雅可比矩阵做对数级数展开$\eqref{eq:duishujishu}$,然后将行列式计算转化为迹的计算$\eqref{eq:det2tr}$,并且利用概率采样的方式$\eqref{eq:tr-caiyang}$,就可以最高效地计算雅可比行列式。
纵观实验效果 #
其实笔者一开始是就被“可逆ResNet”这么美好的构思吸引过来的,但是看到这里,我发现我也怂了,这绝对对得起“硬杠ResNet”的评价呀。本来想对照着好歹实现个mnist的生成来玩玩,后来确认有这么多技巧,如此之暴力,我也放弃了。
所以,还是来看看原论文的实验结果好了。
Toy数据集 #
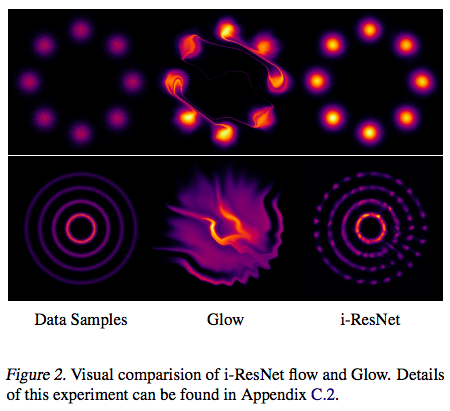
首先是一个人造的Toy数据集,也就是构造一些有规律的随机点来,然后用生成模型去拟合它的分布,GAN中也常做这样的实验。从下图可以看到可逆ResNet的效果比Glow好得多,归根结底,我觉得是因为可逆ResNet是一个很对称的、没有什么偏置的模型,而Glow则是有偏的,它需要我们以某种方式打乱输入,然后对半切分,对半之后两部分的运算是不一样的,这就带来了不对称。
分类任务实验 #
一开始我们就说了,既然是ResNet的一种,最基本的用途就是分类了。下表表明用可逆ResNet做分类任务,效果也是很不错的,Lipschitz约束的存在不会明显影响分类结果(表中的$c$就是$\text{Lip}(g)$)。
生成模型实验 #
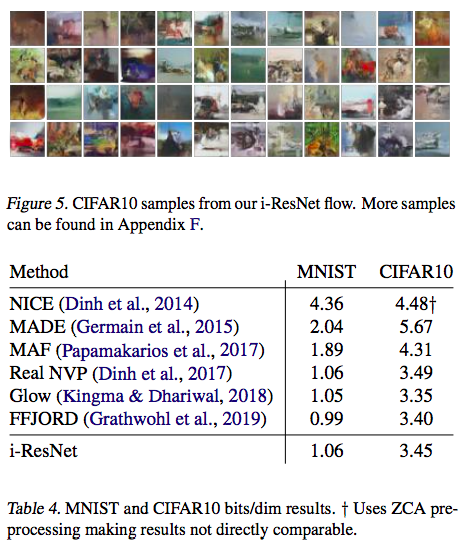
其实流模型系列在生成复杂图片方面还远比不上GAN,但相互之间的定量对比倒没有问题。下图也表明可逆ResNet作为一个基于流的生成模型方面也是很优秀的。
终于可以收工了 #
这样活生生地取硬杠ResNet可真是一件苦力活,我就单纯的解读就已经这么累了,真佩服作者的数学功底。当然,最后作者终究还是成功了,想必成功的喜悦也是很丰盛的。总的来说,整个工作很暴力,但细细品味之下并没有什么违和感,反倒是有一种浑然的美感在里边,并非简单的堆砌数学公式。
唯一的问题是,整个“硬杠”的流程还是挺复杂的,因此要推广使用还是得有好的封装,而这往往就让很多人望而却步了。还有一个问题,就是流模型系列为了保证可逆,自然是不能降维的,但不降维必然就导致计算量大,这是个矛盾的地方。
一个有趣的想法是,对于降维的情形,能不能搞个类似矩阵的“伪逆”那样的模型,来达到类似可逆ResNet的效果呢?非方阵也可以搞个行列式出来的(比如《再谈非方阵的行列式》),因此降维变换也应该能够搞个雅可比行列式的对数出来。貌似不少地方是可以推广过来的。
流模型后面的方向究竟如何呢?让我们拭目以待。
转载到请包括本文地址:https://spaces.ac.cn/archives/6482
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 21, 2019). 《细水长flow之可逆ResNet:极致的暴力美学 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/6482
@online{kexuefm-6482,
title={细水长flow之可逆ResNet:极致的暴力美学},
author={苏剑林},
year={2019},
month={Mar},
url={\url{https://spaces.ac.cn/archives/6482}},
}











March 5th, 2020
这篇里面,用概率统计的手段估计矩阵的迹的方式在 https://arxiv.org/pdf/1810.01367.pdf 中也有用到,苏神有兴趣的话可以看看 文章名字:FFJORD: FREE-FORM CONTINUOUS DYNAMICS FOR SCALABLE REVERSIBLE GENERATIVE MODELS
之前略看了一下,理论上挺有趣,但我现在感觉现在可逆类模型在生成模型上还是没什么前景,所以仅仅保留观望状态。
May 18th, 2020
Hi 博主你好,想请教一个小问题:在Information Bottlenec (IB) 理论里面,信息是要被扔掉一部分的,但这种可逆网络好像和IB的理论相违背,很难去限制信息,。对这一点博主你是怎么看的呢?多谢啦!
相对而言罢了,比如$y=1+0.000001x$是一个线性模型,也就是可逆网络,但是$x$的系数过小,正常来说它都起不了什么作用,所以几乎等价于不可逆的$y=1$。
可逆网络从理论上保证了信息不至于严重退化,但实际训练结果估计还是会收缩到一定程度的(也就是依然存在瓶颈)。
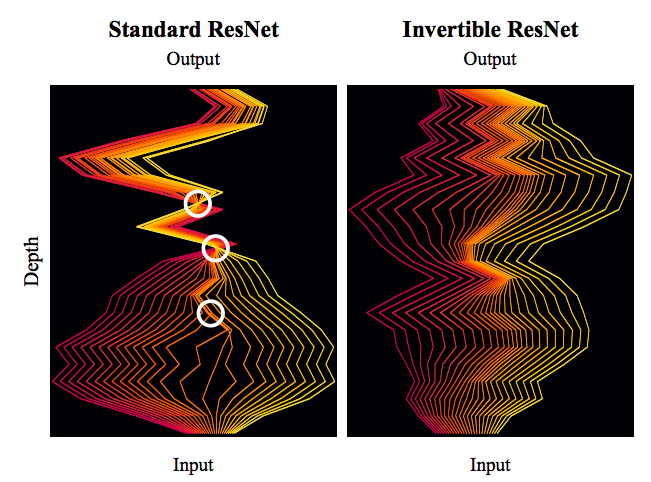
从文章开头的对比图也可以看出,就算是可逆网络传输宽度也不是一直都是那么宽,所以也可以看出会存在“瓶颈”,只不过可能这个“瓶颈”相对而言更宽一些罢了。
之前在网上看到过一个MIT的PPT,里面提到了类似的问题:当你想输出一个N维独立正态分布的时候,你其实在假设输入的数据也是N维的,而不是N维空间中的低维流形。这在大部分情形下不需要考虑,因为数据通常还存在一个非常小的N维噪声。但在有些极端情形下(例如离散的分布),如果不做任何处理,由于要把一个非常窄的分布拉到很宽的分布上,Jacobian的值会变的不收敛。这就会导致模型不稳定,甚至产生Null。一个简单的解决方案就是在数据$x$上叠加一个独立正态分布$w$,即$x'=x+\gamma w$,这个$\gamma$通常比数据小两个数量级。这样就能保证需要的Jacobian不至于特别大。
November 18th, 2020
我之前一直在想,矩阵可以求逆或者伪逆,然后激活函数可以选择(甚至重新构造)一个可逆的标量函数,那么这不就已经可以构造一个可逆网络了吗?至少对于单纯的前向网络来说。在这种情况下,还有必要整这么复杂,凹结构求雅克比行列式?还是说要考虑网络的非线性能力?小弟可逆考虑不周,万请苏神解惑---
敢情写那么多都白写了...
1、伪逆也算逆吗?就算是方阵,一定可逆吗?
2、雅可比行列式怎么算呢?
其实按我的意思,雅克比行列式都不用计算了,但是要算矩阵的逆。$X_2 = WX_1$,$X_3 = f(X_2)$,所以$X_2 = f^{-1}(X_3), X_1 = W^{-1}X_2$。我还是小看了这里面的难度,你说的对,伪逆本身就有很大误差(还未必有唯一解),即便是方阵,也不是那么好搞的。我就说肯定不会这么简单。。。
不算雅可比行列式的话,那几乎任意方阵都可逆了(不可逆意味着行列式严格等于0,对于数值计算来说这几乎是不可能的事情)。我们需要雅可比行列式来保证变换的压缩程度没那么严重(举个例子,y=0.0000000000001x也是可逆的,但这种可逆没什么价值,几乎相当于不可逆)
你举的这个例子,是指激活函数的时候,还是说矩阵变换的时候呢?如果是激活,那么它就是一个标量函数,我们应该可以设计一个函数,让既有适当的非线性,而且还可逆。。。的吧?如果是指矩阵变换,这我就不懂了,因为某一个系数特别小,就把它截断为0呗;某系数乘某x得到的某y特别小,也可以截断啊。这个线性变换应该不影响整体效果吧,所以重点还是在非线性变换上。愚想拙见,让方家见笑了--
矩阵变换。
截断为零不就不可逆了么?
December 25th, 2022
苏神提到了封装的问题,我在去年其实就做了一整套的封装(https://github.com/ELIFE-ASU/INNLab),包括线性、非线性、卷积层。不过我的包里没有i-ResNet,因为这几个作者很快就搞出了更好的ResidualFlow(i-ResNet在估计Jacobian的时候,如果维度很高,是有偏差的,而ResFlow则不会有)。代码一个人写的,难免有错漏,欢迎苏神来指正。
感谢推荐,赞一个。好久不做flow相关了,debug可能就帮不上忙了,抱歉~
April 14th, 2024
很漂亮的工作,19年的Invertible Auto-Encoders还有20年的Rectangular Flows都是可以降维的。