均匀球状星团内恒星的运动
By 苏剑林 | 2011-07-08 | 21013位读者 | 引用我们考虑一个球状的星团,并假设它是各向同性的,即距离球心r处的物质密度ρ只与r有关,ρ=ρ(r)。那么,在半径为r的球形区域内的总质量为:
$$M(r)=\int_0^r 4\pi x^2 \rho(x) dx$$
想象有一颗质量比较小的恒星(其实相对于星团总质量,每一颗恒星的质量都很小)在星团的引力作用下运动(就好像太阳系绕着银河系运动一样),且恒星并没有受到其他物质(如星际尘埃等)的阻力。我们之前已经证明过,各向同性的球壳内部的引力是为0的,那么这种情况下的运动就相当于恒星只受到它到球心处的一个球形区域内的质量的引力吸引。根据万有引力定律,选择星团球心为参考系,可以得出
$$\ddot{\vec{r}}=-GM(r)\frac{\vec{r}}{r^3}$$
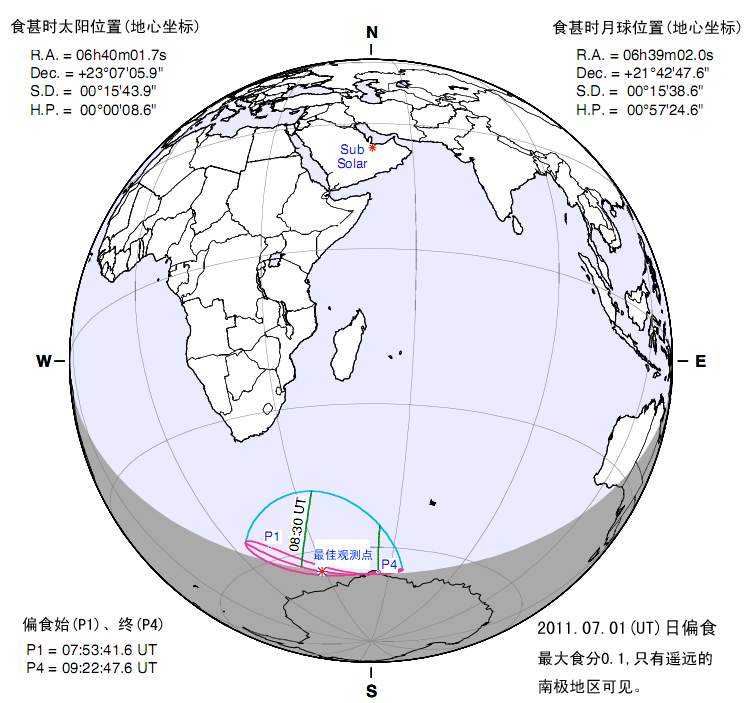
科学空间:2011年7月重要天象
By 苏剑林 | 2011-07-06 | 27609位读者 | 引用最近的那些事儿...
By 苏剑林 | 2011-07-05 | 18175位读者 | 引用cos 1°的根式表达式
By 苏剑林 | 2011-06-26 | 75902位读者 | 引用BoJone记得自己第一次接触三角函数大概是小学五、六年级的时候,那时候我拿来了表姐的初中数学书来看。看到三角函数一章后,饶有兴致,希望能够找到一个根据角度来求三角函数值的方法,可是书本上只是教我去用计算器算和查表,这让我这个爱好计算的孩子大失所望。这个问题直到高一才得以解决,原来这已经涉及到了微积分中的泰勒级数了...
我记得为了求任意角度的三角函数值,我曾经根据30°、45°和60°的正弦值拟合过一条近似公式出来:
$$\sin A \approx \sqrt{\frac{A}{60}-1/4}$$
其中A以角度为单位,大致适用于25°~60°,精度好像有两位小数。当然,这个结果在今天看来是很粗糙的,但是这毕竟是我的“小学的作品”!在此留念一翻。
高中数学联赛题目和答案
By 苏剑林 | 2011-06-25 | 32509位读者 | 引用2011年的高中数学联赛拉开帷幕了...
前些天数学老师找了我们两个重点班的8个人,商量了参加今年数学联赛预赛的事情。大家都同意尝试,同时在我的强烈要求之下,增加了两位同学(一位是我的同桌,另外一位是我心目中的“天才生”)。只是老师也没有组织经验,而我上一年有过参赛经验(本来那是高三的玩意儿,我那时一个高二生瞎搅和进去,居然把高三的几个师兄师姐P下去了,意外呀...^_^),老师就把辅导其他九位同学的任务交给我(艰巨...)。
其实我也没有累积多少数学竞赛的知识,我最感兴趣的数学,几乎都不能在数学竞赛中用到。不过既然报名了,还是得准备准备,因此在网上找了最近几年的高中数学联赛试题和答案来看。顺便放到这里共享,供有需要的朋友下载。
向量结合复数:常曲率曲线(1)
By 苏剑林 | 2011-06-19 | 36979位读者 | 引用在之前的一篇向量系列的文章中,我们通过结合物理与向量来巧妙地推导出了曲线(包括平面和空间的)的曲率半径为
$$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}\tag{1}$$
曲率则是曲率半径的导数:$\rho=\frac{1}{R}$。我们反过来思考一下:曲率恒定的平面曲线是否只有圆?
答案貌似是很显然的,我们需要证明一下。
由于只是考虑平面情况,我们先设$\dot{\vec{r}}=(v cos\theta,v sin\theta)=z=ve^{i\theta}$,代入(1)得到
$\frac{\dot{\theta}}{v}=\rho$————(2)
只要我们曾经拥有过——《萍聚》
By 苏剑林 | 2011-06-06 | 29104位读者 | 引用这首歌是凤儿介绍的,去年我们学校高一夏令营的“主题歌曲”。她说歌词写得很好,我感觉也挺不错的^_^
萍,指的是漂浮在水面上的一种藻类,风吹过来,它们就会在风的作用力下聚在一起。人好象是浮在水面上的荷叶,聚散不过都是风吹动所致,到处飘散而已。因此便有了“萍水相逢”这一成语,指的是无心的邂逅或偶然的相遇。“萍聚”亦然。
曾有宋词写道“风中柳絮水中萍,聚散两无情”,这便让我们倍感人生悲欢离合的无奈。在这个充斥着高考的离别的六月里,离愁味道更浓了。可是,不论如何,明天的事情与我们无关,我们要珍惜今天事,珍惜今天人,尽我所能把握好我所拥有的。正如——
Cherish someone special for you and let them know you cherish them.
这样,当我们真的面临无可奈何的离别时,也能够含泪而微笑地挥手,唱着“只要我们曾经拥有过...”。这就是《萍聚》的声音!









最近评论