生成扩散模型漫谈（四）：DDIM = 高观点DDPM

相信很多读者都听说过甚至读过克莱因的《高观点下的初等数学》这套书，顾名思义，这是在学到了更深入、更完备的数学知识后，从更高的视角重新审视过往学过的初等数学，以得到更全面的认知，甚至达到温故而知新的效果。类似的书籍还有很多，比如《重温微积分》、《复分析：可视化方法》等。

回到扩散模型，目前我们已经通过三篇文章从不同视角去解读了DDPM，那么它是否也存在一个更高的理解视角，让我们能从中得到新的收获呢？当然有，《Denoising Diffusion Implicit Models》介绍的DDIM模型就是经典的案例，本文一起来欣赏它。

思路分析 #

在《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》中，我们提到过该文章所介绍的推导跟DDIM紧密相关。具体来说，文章的推导路线可以简单归纳如下：
\begin{equation}p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})\xrightarrow{\text{推导}}p(\boldsymbol{x}_t|\boldsymbol{x}_0)\xrightarrow{\text{推导}}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)\xrightarrow{\text{近似}}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\end{equation}
这个过程是一步步递进的。然而，我们发现最终结果有着两个特点：

1、损失函数只依赖于$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$；

2、采样过程只依赖于$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$。

也就是说，尽管整个过程是以$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$为出发点一步步往前推的，但是从结果上来看，压根儿就没$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$的事。那么，我们大胆地“异想天开”一下：

高观点1： 既然结果跟$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$无关，可不可以干脆“过河拆桥”，将$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$从整个推导过程中去掉？

DDIM正是这个“异想天开”的产物！

待定系数 #

可能有读者会想，根据上一篇文章所用的贝叶斯定理
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}{p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\end{equation}
没有给定$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$怎么能得到$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$？这其实是思维过于定式了，理论上在没有给定$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$的情况下，$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的解空间更大，某种意义上来说是更加容易推导，此时它只需要满足边际分布条件：
\begin{equation}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\label{eq:margin}\end{equation}
我们用待定系数法来求解这个方程。在上一篇文章中，所解出的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$是一个正态分布，所以这一次我们可以更一般地设
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}(\boldsymbol{x}_{t-1}; \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I})\end{equation}
其中$\kappa_t,\lambda_t,\sigma_t$都是待定系数，而为了不重新训练模型，我们不改变$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$和$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$，于是我们可以列出
\begin{array}{c|c|c}
\hline
\text{记号} & \text{含义} & \text{采样}\\
\hline
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_{t-1};\bar{\alpha}_{t-1} \boldsymbol{x}_0,\bar{\beta}_{t-1}^2 \boldsymbol{I}) & \boldsymbol{x}_{t-1} = \bar{\alpha}_{t-1} \boldsymbol{x}_0 + \bar{\beta}_{t-1} \boldsymbol{\varepsilon} \\
\hline
p(\boldsymbol{x}_t|\boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I}) & \boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}_1 \\
\hline
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) & \mathcal{N}(\boldsymbol{x}_{t-1}; \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I}) & \boldsymbol{x}_{t-1} = \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\
\hline
{\begin{array}{c}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) \\
p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t\end{array}} & & {\begin{aligned}\boldsymbol{x}_{t-1} =&\, \kappa_t \boldsymbol{x}_t + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\
=&\, \kappa_t (\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}_1) + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\varepsilon}_2 \\
=&\, (\kappa_t \bar{\alpha}_t + \lambda_t) \boldsymbol{x}_0 + (\kappa_t\bar{\beta}_t \boldsymbol{\varepsilon}_1 + \sigma_t \boldsymbol{\varepsilon}_2) \\
\end{aligned}} \\
\hline
\end{array}
其中$\boldsymbol{\varepsilon},\boldsymbol{\varepsilon}_1,\boldsymbol{\varepsilon}_2\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$，并且由正态分布的叠加性我们知道$\kappa_t\bar{\beta}_t \boldsymbol{\varepsilon}_1 + \sigma_t \boldsymbol{\varepsilon}_2\sim \sqrt{\kappa_t^2\bar{\beta}_t^2 + \sigma_t^2} \boldsymbol{\varepsilon}$。对比$\boldsymbol{x}_{t-1}$的两个采样形式，我们发现要想$\eqref{eq:margin}$成立，只需要满足两个方程
\begin{equation}\bar{\alpha}_{t-1} = \kappa_t \bar{\alpha}_t + \lambda_t, \qquad\bar{\beta}_{t-1} = \sqrt{\kappa_t^2\bar{\beta}_t^2 + \sigma_t^2}\end{equation}
可以看到有三个未知数，但只有两个方程，这就是为什么说没有给定$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$时解空间反而更大了。将$\sigma_t$视为可变参数，可以解出
\begin{equation}\kappa_t = \frac{\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t},\qquad \lambda_t = \bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}\end{equation}
或者写成
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t} \boldsymbol{x}_t + \left(\bar{\alpha}_{t-1} - \frac{\bar{\alpha}_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t}\right) \boldsymbol{x}_0, \sigma_t^2 \boldsymbol{I}\right)\label{eq:p-xt-x0}\end{equation}
方便起见，我们约定$\bar{\alpha}_0=1, \bar{\beta}_0=0$。特别地，这个结果并不需要限定$\bar{\alpha}_t^2 + \bar{\beta}_t^2 = 1$，不过为了简化参数设置，同时也为了跟以往的结果对齐，这里还是约定$\bar{\alpha}_t^2 + \bar{\beta}_t^2 = 1$。

一如既往 #

现在我们在只给定$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$、$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$的情况下，通过待定系数法求解了$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的一簇解，它带有一个自由参数$\sigma_t$。用《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》中的“拆楼-建楼”类比来说，就是我们知道楼会被拆成什么样【$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$、$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$】，但是不知道每一步怎么拆【$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$】，然后希望能够从中学会每一步怎么建【$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$】。当然，如果我们想看看每一步怎么拆的话，也可以反过来用贝叶斯公式
\begin{equation} p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_t|\boldsymbol{x}_0)}{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}\end{equation}

接下来的事情，就跟上一篇文章一模一样了：我们最终想要$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$而不是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$，所以我们希望用
\begin{equation}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t) = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\end{equation}
来估计$\boldsymbol{x}_0$，由于没有改动$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$，所以训练所用的目标函数依然是$\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2$（除去权重系数），也就是说训练过程没有改变，我们可以用回DDPM训练好的模型。而用$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$替换掉式$\eqref{eq:p-xt-x0}$中的$\boldsymbol{x}_0$后，得到
\begin{equation}\begin{aligned}
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx&\, p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) \\
=&\, \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t\sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right), \sigma_t^2 \boldsymbol{I}\right)
\end{aligned}\label{eq:p-xt-x0-2}\end{equation}
这就求出了生成过程所需要的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$，其中$\alpha_t=\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$。它的特点是训练过程没有变化（也就是说最终保存下来的模型没有变化），但生成过程却有一个可变动的参数$\sigma_t$，就是这个参数给DDPM带来了新鲜的结果。

几个例子 #

原则上来说，我们对$\sigma_t$没有过多的约束，但是不同$\sigma_t$的采样过程会呈现出不同的特点，我们举几个例子进行分析。

第一个简单例子就是取$\sigma_t = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}$，其中$\beta_t = \sqrt{1 - \alpha_t^2}$，相应地有
\begin{equation}\small{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \frac{\beta_t^2}{\bar{\beta}_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)}\label{eq:choice-1}\end{equation}
这就是上一篇文章所推导的DDPM。特别是，DDIM论文中还对$\sigma_t = \eta\frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}$做了对比实验，其中$\eta\in[0, 1]$。

第二个例子就是取$\sigma_t = \beta_t$，这也是前两篇文章所指出的$\sigma_t$的两个选择之一，在此选择下式$\eqref{eq:p-xt-x0-2}$未能做进一步的化简，但DDIM的实验结果显示此选择在DDPM的标准参数设置下表现还是很好的。

最特殊的一个例子是取$\sigma_t = 0$，此时从$\boldsymbol{x}_t$到$\boldsymbol{x}_{t-1}$是一个确定性变换
\begin{equation}\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \left(\bar{\beta}_t - \alpha_t \bar{\beta}_{t-1}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\label{eq:sigma=0}\end{equation}
这也是DDIM论文中特别关心的一个例子，准确来说，原论文的DDIM就是特指$\sigma_t=0$的情形，其中“I”的含义就是“Implicit”，意思这是一个隐式的概率模型，因为跟其他选择所不同的是，此时从给定的$\boldsymbol{x}_T = \boldsymbol{z}$出发，得到的生成结果$\boldsymbol{x}_0$是不带随机性的。后面我们将会看到，这在理论上和实用上都带来了一些好处。

加速生成 #

值得指出的是，在这篇文章中我们没有以$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$为出发点，所以前面的所有结果实际上全都是以$\bar{\alpha}_t,\bar{\beta}_t$相关记号给出的，而$\alpha_t,\beta_t$则是通过$\alpha_t=\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$和$\beta_t = \sqrt{1 - \alpha_t^2}$派生出来的记号。从损失函数$\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2$可以看出，给定了各个$\bar{\alpha}_t$，训练过程也就确定了。

从这个过程中，DDIM进一步留意到了如下事实：

高观点2： DDPM的训练结果实质上包含了它的任意子序列参数的训练结果。

具体来说，设$\boldsymbol{\tau} = [\tau_1,\tau_2,\dots,\tau_{\dim(\boldsymbol{\tau})}]$是$[1,2,\cdots,T]$的任意子序列，那么我们以$\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})}$为参数训练一个扩散步数为$\dim(\boldsymbol{\tau})$步的DDPM，其目标函数实际上是原来以$\bar{\alpha}_1,\bar{\alpha}_2,\cdots,\bar{\alpha}_T$的$T$步DDPM的目标函数的一个子集！所以在模型拟合能力足够好的情况下，它其实包含了任意子序列参数的训练结果。

那么反过来想，如果有一个训练好的$T$步DDPM模型，我们也可以将它当成是以$\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})}$为参数训练出来的$\dim(\boldsymbol{\tau})$步模型，而既然是$\dim(\boldsymbol{\tau})$步的模型，生成过程也就只需要$\dim(\boldsymbol{\tau})$步了，根据式$\eqref{eq:p-xt-x0-2}$有：
\begin{equation}p(\boldsymbol{x}_{\tau_{i-1}}|\boldsymbol{x}_{\tau_i}) \approx \mathcal{N}\left(\boldsymbol{x}_{\tau_{i-1}}; \frac{\bar{\alpha}_{\tau_{i-1}}}{\bar{\alpha}_{\tau_i}}\left(\boldsymbol{x}_{\tau_i} - \left(\bar{\beta}_{\tau_i} - \frac{\bar{\alpha}_{\tau_i}}{\bar{\alpha}_{\tau_{i-1}}}\sqrt{\bar{\beta}_{\tau_{i-1}}^2 - \tilde{\sigma}_{\tau_i}^2}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_{\tau_i}, \tau_i)\right), \tilde{\sigma}_{\tau_i}^2 \boldsymbol{I}\right)\end{equation}
这就是加速采样的生成过程了，从原来的$T$步扩散生成变成了$\dim(\boldsymbol{\tau})$步。要注意不能直接将式$\eqref{eq:p-xt-x0-2}$的$\alpha_t$换成$\alpha_{\tau_i}$，因为我们说过$\alpha_t$是派生记号而已，它实际上等于$\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$，因此$\alpha_t$要换成$\frac{\bar{\alpha}_{\tau_i}}{\bar{\alpha}_{\tau_{i-1}}}$才对。同理，$\tilde{\sigma}_{\tau_i}$也不是直接取$\sigma_{\tau_i}$，而是在将其定义全部转化为$\bar{\alpha},\bar{\beta}$符号后，将$t$替换为$\tau_i$、$t-1$替换为$\tau_{i-1}$，比如式$\eqref{eq:choice-1}$对应的$\tilde{\sigma}_{\tau_i}$为
\begin{equation}\sigma_t = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}=\frac{\bar{\beta}_{t-1}}{\bar{\beta}_t}\sqrt{1 - \frac{\bar{\alpha}_t^2}{\bar{\alpha}_{t-1}^2}}\quad\to\quad\frac{\bar{\beta}_{\tau_{i-1}}}{\bar{\beta}_{\tau_i}}\sqrt{1 - \frac{\bar{\alpha}_{\tau_i}^2}{\bar{\alpha}_{\tau_{i-1}}^2}}=\tilde{\sigma}_{\tau_i}\end{equation}

可能读者又想问，我们为什么干脆不直接训练一个$\dim(\boldsymbol{\tau})$步的扩散模型，而是要先训练$T > \dim(\boldsymbol{\tau})$步然后去做子序列采样？笔者认为可能有两方面的考虑：一方面从$\dim(\boldsymbol{\tau})$步生成来说，训练更多步数的模型也许能增强泛化能力；另一方面，通过子序列$\boldsymbol{\tau}$进行加速只是其中一种加速手段，训练更充分的$T$步允许我们尝试更多的其他加速手段，但并不会显著增加训练成本。

实验结果 #

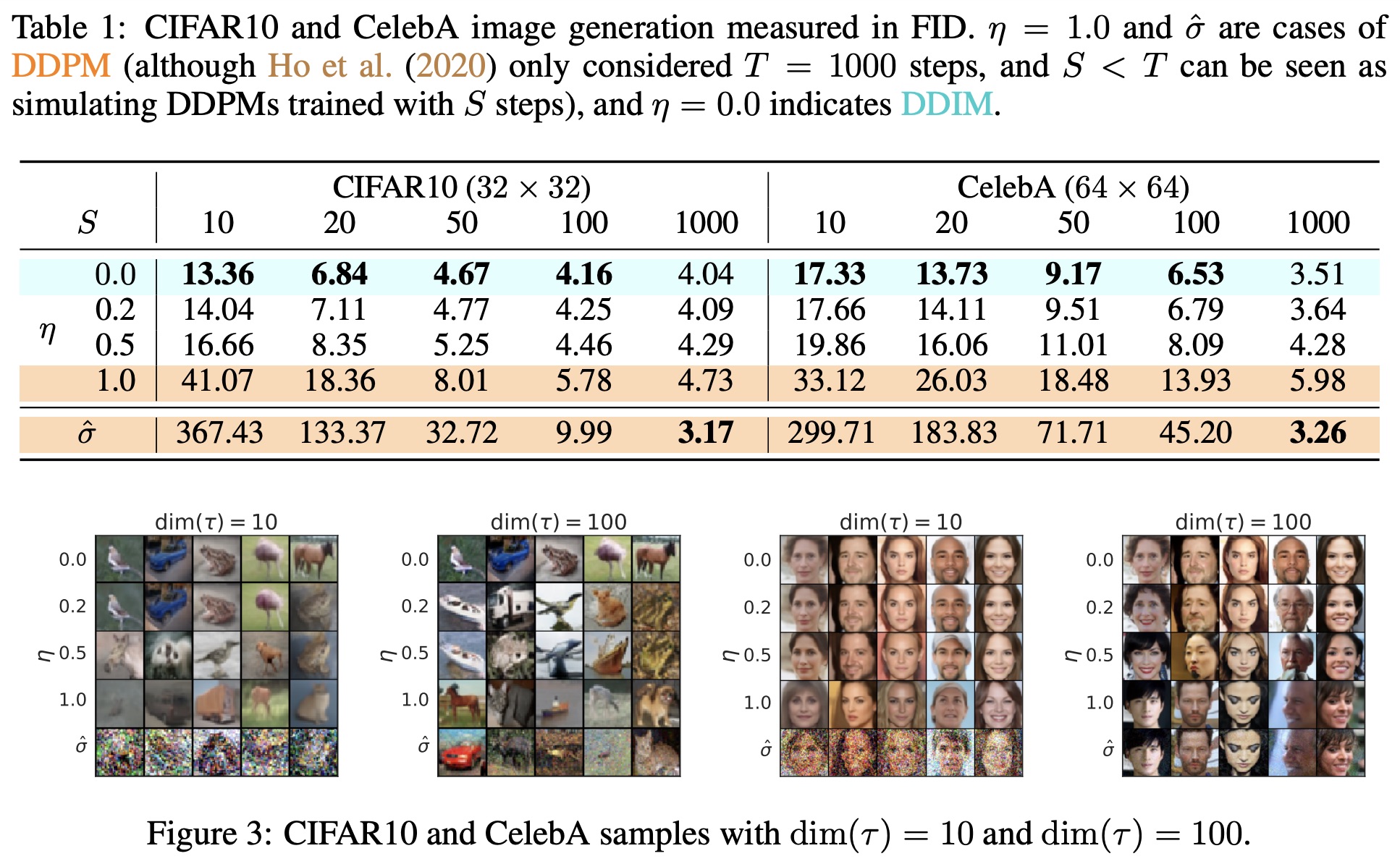
原论文对不同的噪声强度和扩散步数$\dim(\boldsymbol{\tau})$做了组合对比，大致上的结果是“噪声越小，加速后的生成效果越好”，如下图

DDIM的实验结果，显示噪声越小，加速后的生成效果越好

笔者的参考实现如下：

Github：https://github.com/bojone/Keras-DDPM/blob/main/ddim.py

个人的实验结论是：

1、可能跟直觉相反，生成过程中的$\sigma_t$越小，最终生成图像的噪声和多样性反而相对来说越大；

2、扩散步数$\dim(\boldsymbol{\tau})$越少，生成的图片更加平滑，多样性也会有所降低；

3、结合1、2两点得知，在扩散步数$\dim(\boldsymbol{\tau})$减少时，可以适当缩小$\sigma_t$，以保持生成图片质量大致不变，这跟DDIM原论文的实验结论是一致的；

4、在$\sigma_t$较小时，相比可训练的Embedding层，用固定的Sinusoidal编码来表示$t$所生成图片的噪声要更小；

5、在$\sigma_t$较小时，原论文的U-Net架构（Github中的ddpm2.py）要比笔者自行构思的U-Net架构（Github中的ddpm.py）所生成图片的噪声要更小；

6、但个人感觉，总体来说不带噪声的生成过程的生成效果不如带噪声的生成过程，不带噪声时生成效果受模型架构影响较大。

此外，对于$\sigma_t=0$时的DDIM，它就是将任意正态噪声向量变换为图片的一个确定性变换，这已经跟GAN几乎一致了，所以跟GAN类似，我们可以对噪声向量进行插值，然后观察对应的生成效果。但要注意的是，DDPM或DDIM对噪声分布都比较敏感，所以我们不能用线性插值而要用球面插值，因为由正态分布的叠加性，如果$\boldsymbol{z}_1,\boldsymbol{z}_2\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$，$\lambda\boldsymbol{z}_1 + (1-\lambda)\boldsymbol{z}_2$一般就不服从$\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$，要改为
\begin{equation}\boldsymbol{z} = \boldsymbol{z}_1 \cos\frac{\lambda\pi}{2} + \boldsymbol{z}_2 \sin\frac{\lambda\pi}{2},\quad \lambda\in[0, 1]\end{equation}

插值效果演示（笔者自己训练的模型）：

DDIM随机向量的插值生成效果

微分方程 #

最后，我们来重点分析一下$\sigma_t = 0$的情形。此时$\eqref{eq:sigma=0}$可以等价地改写成：
\begin{equation}\frac{\boldsymbol{x}_t}{\bar{\alpha}_t} - \frac{\boldsymbol{x}_{t-1}}{\bar{\alpha}_{t-1}} = \left(\frac{\bar{\beta}_t}{\bar{\alpha}_t} - \frac{\bar{\beta}_{t-1}}{\bar{\alpha}_{t-1}}\right) \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\end{equation}
当$T$足够大，或者说$\alpha_t$与$\alpha_{t-1}$足够小时，我们可以将上式视为某个常微分方程的差分形式。特别地，引入虚拟的时间参数$s$，我们得到
\begin{equation}\frac{d}{ds}\left(\frac{\boldsymbol{x}(s)}{\bar{\alpha}(s)}\right) = \boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}(s), t(s)\right)\frac{d}{ds}\left(\frac{\bar{\beta}(s)}{\bar{\alpha}(s)}\right)\label{eq:ode}\end{equation}
不失一般性，假设$s\in[0,1]$，其中$s=0$对应$t=0$、$s=1$对应$t=T$。注意DDIM原论文直接用$\frac{\bar{\beta}(s)}{\bar{\alpha}(s)}$作为虚拟时间参数，这原则上是不大适合的，因为它的范围是$[0,\infty)$，无界的区间不利于数值求解。

那么现在我们要做的事情就是在给定$\boldsymbol{x}(1)\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$的情况下，去求解出$\boldsymbol{x}(0)$。而DDPM或者DDIM的迭代过程，对应于该常微分方程的欧拉方法。众所周知欧拉法的效率相对来说是最慢的，如果要想加速求解，可以用Heun方法、R-K方法等。也就是说，将生成过程等同于求解常微分方程后，可以借助常微分方程的数值解法，为生成过程的加速提供更丰富多样的手段。

以DDPM的默认参数$T=1000$、$\alpha_t = \sqrt{1 - \frac{0.02t}{T}}$为例，我们重复《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》所做的估计
\begin{equation}\log \bar{\alpha}_t = \sum_{i=k}^t \log\alpha_k = \frac{1}{2} \sum_{k=1}^t \log\left(1 - \frac{0.02k}{T}\right) < \frac{1}{2} \sum_{k=1}^t \left(- \frac{0.02k}{T}\right) = -\frac{0.005t(t+1)}{T}\end{equation}
事实上，由于每个$\alpha_k$都很接近于1，所以上述估计其实也是一个很好的近似。而我们说了本文的出发点是$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$，所以应该以$\bar{\alpha}_t$为起点，根据上述近似，我们可以直接简单地取
\begin{equation}\bar{\alpha}_t = \exp\left(-\frac{0.005t^2}{T}\right) = \exp\left(-\frac{5t^2}{T^2}\right)\end{equation}
如果取$s=t/T$为参数，那么正好$s\in[0,1]$，此时$\bar{\alpha}(s)=e^{-5s^2}$，代入到式$\eqref{eq:ode}$化简得
\begin{equation}\frac{d\boldsymbol{x}(s)}{ds} = 10s\left(\frac{\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}(s), sT\right)}{\sqrt{1-e^{-10s^2}}} - \boldsymbol{x}(s)\right)\end{equation}
也可以取$s=t^2/T^2$为参数，此时也有$s\in[0,1]$，以及$\bar{\alpha}(s)=e^{-5s}$，代入到式$\eqref{eq:ode}$化简得
\begin{equation}\frac{d\boldsymbol{x}(s)}{ds} = 5\left(\frac{\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}(s), \sqrt{s}T\right)}{\sqrt{1-e^{-10s}}} - \boldsymbol{x}(s)\right)\end{equation}

文章小结 #

本文接着上一篇DDPM的推导思路来介绍了DDIM，它重新审视了DDPM的出发点，去掉了推导过程中的$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$，从而获得了一簇更广泛的解和加速生成过程的思路，最后这簇新解还允许我们将生成过程跟常微分方程的求解联系起来，从而借助常微分方程的方法进一步对生成过程进行研究。

转载到请包括本文地址：https://spaces.ac.cn/archives/9181

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。