Google新作Synthesizer：我们还不够了解自注意力

深度学习这个箱子，远比我们想象的要黑。

写在开头 #

据说物理学家费曼说过一句话^[来源]：“谁要是说他懂得量子力学，那他就是真的不懂量子力学。”我现在越来越觉得，这句话中的“量子力学”也可以替换为“深度学习”。尽管深度学习已经在越来越多的领域证明了其有效性，但我们对它的解释性依然相当无力。当然，这几年来已经有不少工作致力于打开深度学习这个黑箱，但是很无奈，这些工作基本都是“马后炮”式的，也就是在已有的实验结果基础上提出一些勉强能说服自己的解释，无法做到自上而下的构建和理解模型的原理，更不用说提出一些前瞻性的预测。

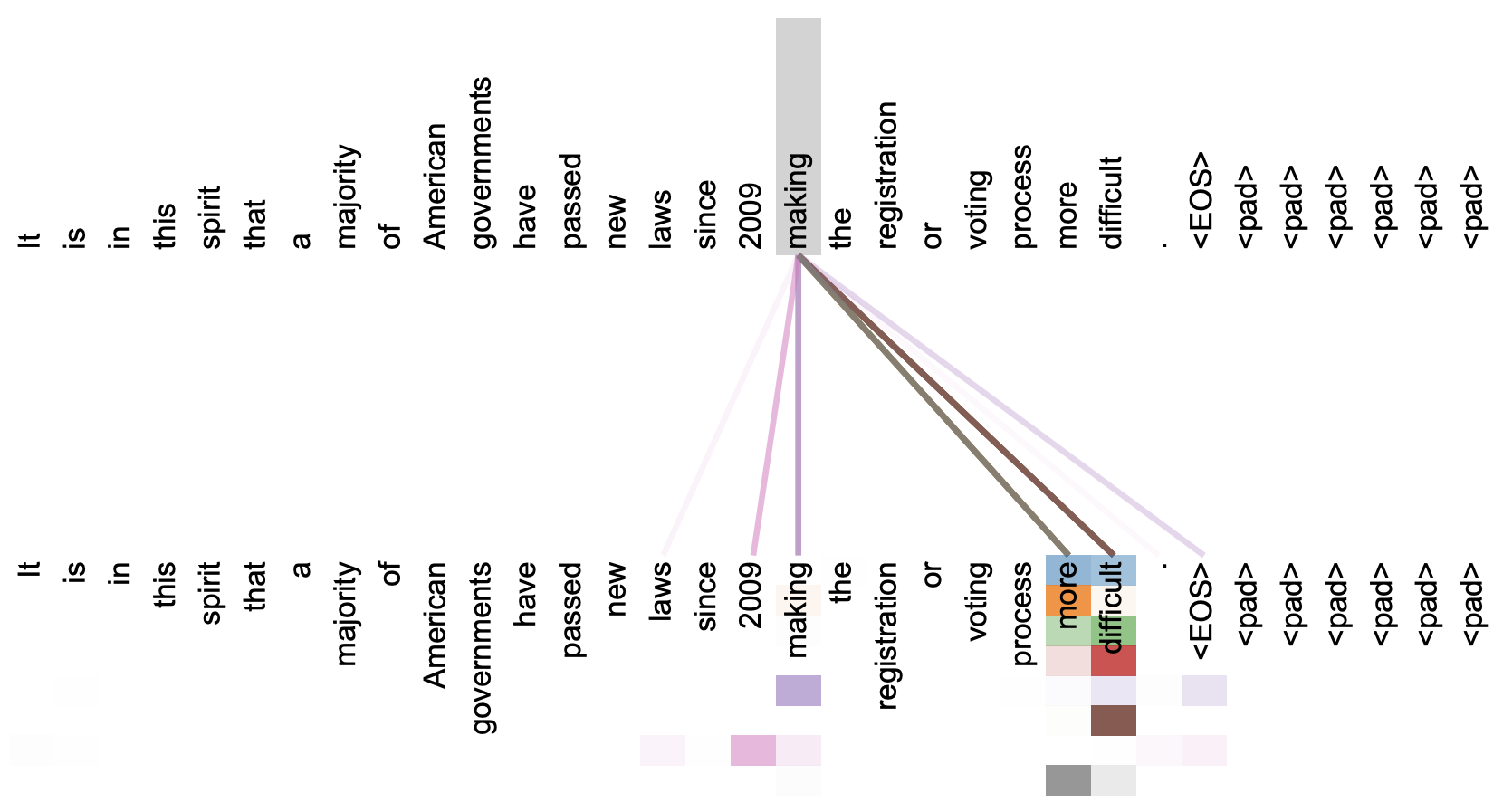
本文关注的是自注意力机制。直观上来看，自注意力机制算是解释性比较强的模型之一了，它通过自己与自己的Attention来自动捕捉了token与token之间的关联，事实上在《Attention is All You Need》那篇论文中，就给出了如下的看上去挺合理的可视化效果：

《Attention is All You Need》一文中对Attention的可视化例子

但自注意力机制真的是这样生效的吗？这种“token对token”的注意力是必须的吗？前不久Google的新论文《Synthesizer: Rethinking Self-Attention in Transformer Models》对自注意力机制做了一些“异想天开”的探索，里边的结果也许会颠覆我们对自注意力的认知。

自注意力 #

自注意力模型的流行，始于2017年Google发表的《Attention is All You Need》一文，关于它的科普读者还可以参考笔者旧作《Attention is All You Need》浅读（简介+代码）。它的基础是Scaled-Dot Attention，定义如下：
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\end{equation}
其中$\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$，softmax则是在$m$的那一维进行归一化。而自注意力，则是对于同一个$\boldsymbol{X}\in \mathbb{R}^{n\times d}$，通过不同的投影矩阵$\boldsymbol{W}_q,\boldsymbol{W}_k,\boldsymbol{W}_v\in\mathbb{R}^{d\times d'}$得到$\boldsymbol{Q}=\boldsymbol{X}\boldsymbol{W}_q,\boldsymbol{K}=\boldsymbol{X}\boldsymbol{W}_k,\boldsymbol{V}=\boldsymbol{X}\boldsymbol{W}_v$，然后再做Attention，即
\begin{equation}\begin{aligned}
SelfAttention(\boldsymbol{X}) =&\, Attention(\boldsymbol{X}\boldsymbol{W}_q, \boldsymbol{X}\boldsymbol{W}_k, \boldsymbol{X}\boldsymbol{W}_v)\\
=&\, softmax\left(\frac{\boldsymbol{X}\boldsymbol{W}_q \boldsymbol{W}_k^{\top}\boldsymbol{X}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{X}\boldsymbol{W}_v&
\end{aligned}\end{equation}
至于Multi-Head Attention，则不过是Attention运算在不同的参数下重复多次然后将多个输出拼接起来，属于比较朴素的增强。而关于它的进一步推广，则可以参考《突破瓶颈，打造更强大的Transformer》。

天马行空 #

本质上来看，自注意力就是通过一个$n\times n$的矩阵$\boldsymbol{A}$和$d\times d'$的矩阵$\boldsymbol{W}_v$，将原本是$n\times d$的矩阵$\boldsymbol{X}$，变成了$n\times d'$的矩阵$\boldsymbol{A}\boldsymbol{X}\boldsymbol{W}_v$。其中矩阵$\boldsymbol{A}$是动态生成的，即
\begin{equation}\boldsymbol{A}=softmax\left(\boldsymbol{B}\right),\quad\boldsymbol{B}=\frac{\boldsymbol{X}\boldsymbol{W}_q \boldsymbol{W}_k^{\top}\boldsymbol{X}^{\top}}{\sqrt{d_k}}\end{equation}
对于矩阵$\boldsymbol{B}$，本质上来说它就是$\boldsymbol{X}$里边两两向量的内积组合，所以我们称它为“token对token”的Attention。

Synthesizer自注意力与标准自注意力的对比

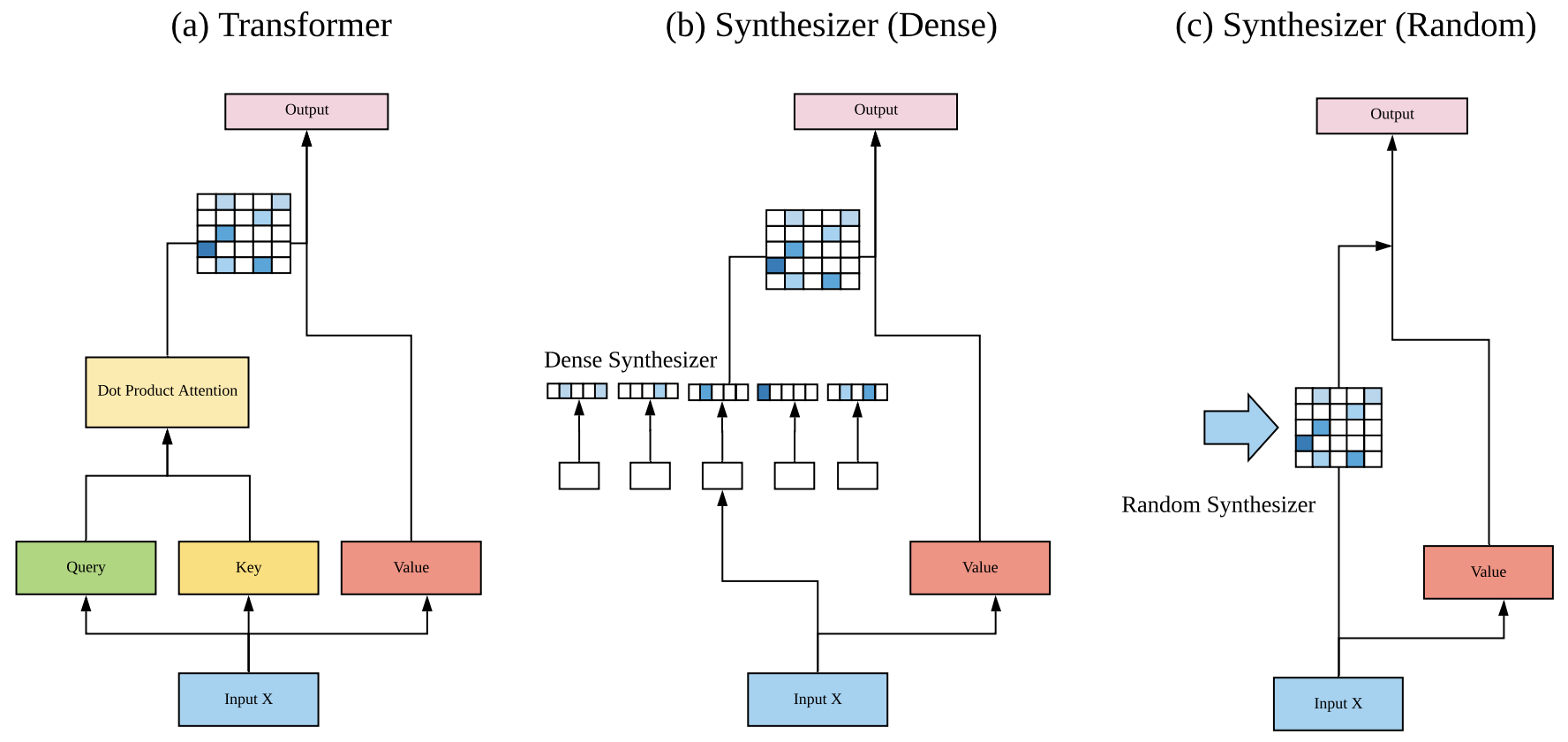
那么，就到了前面提出的问题：“token对token”是必须的吗？能不能通过其他方式来生成这个矩阵$\boldsymbol{B}$？Google的这篇论文正是“天马行空”了几种新的形式并做了实验，这些形式统称为Synthesizer。

Dense形式 #

第一种形式在原论文中称为Dense：$\boldsymbol{B}$需要是$n\times n$大小的，而$\boldsymbol{X}$是$n\times d$的，所以只需要一个$d\times n$的变换矩阵$\boldsymbol{W}_a$就可以将它变成$n\times n$了，即
\begin{equation}\boldsymbol{B}=\boldsymbol{X}\boldsymbol{W}_a\end{equation}
这其实就相当于把$\boldsymbol{K}$固定为常数矩阵$\boldsymbol{W}_a^{\top}$了。当然，原论文还做得更复杂一些，用到了两层Dense层：
\begin{equation}\boldsymbol{B}=\text{relu}\left(\boldsymbol{X}\boldsymbol{W}_1 + \boldsymbol{b}_1\right)\boldsymbol{W}_2 + \boldsymbol{b}_2\end{equation}
但思想上并没有什么变化。

Random形式 #

刚才说Dense形式相当于把$\boldsymbol{K}$固定为常数矩阵，我们还能不能更“异想天开”一些：把$\boldsymbol{Q}$固定为常数矩阵？这时候整个$\boldsymbol{B}$相当于是一个常数矩阵，即
\begin{equation}\boldsymbol{B}=\boldsymbol{R}\end{equation}
原论文中还真是实验了这种形式，称之为Random，顾名思义，就是$\boldsymbol{B}$是随机初始化的，然后可以选择随训练更新或不更新。据原论文描述，固定形式的Attention首次出现在论文《Fixed Encoder Self-Attention Patterns in Transformer-Based Machine Translation》，不同点是那里的Attention矩阵是由一个函数算出来的，而Google这篇论文则是完全随机初始化的。从形式上看，Random实际上就相当于可分离卷积（Depthwise Separable Convolution）运算。

低秩分解 #

上面两种新形式，往往会面对着参数过多的问题，所以很自然地就想到通过低秩分解来降低参数量。对于Dense和Random，原论文也提出并验证了对应的低秩分解形式，分别称为Factorized Dense和Factorized Random。

Factorized Dense通过Dense的方式，生成两个$n\times a, n\times b$的矩阵$\boldsymbol{B}_1,\boldsymbol{B}_2$，其中$ab=n$；然后将$\boldsymbol{B}_1$重复$b$次、然后将$\boldsymbol{B}_2$重复$a$次，得到对应的$n\times n$矩阵$\tilde{\boldsymbol{B}}_1,\tilde{\boldsymbol{B}}_2$，最后将它们逐位相乘（个人感觉相乘之前$\tilde{\boldsymbol{B}}_2$应该要转置一下比较合理，但原论文并没有提及），合成一个$n\times n$的矩阵：
\begin{equation}\boldsymbol{B}=\tilde{\boldsymbol{B}}_1 \otimes \tilde{\boldsymbol{B}}_2\end{equation}

至于Factorized Random就很好理解了，本来是一整个$n\times n$的矩阵$\boldsymbol{R}$，现在变成两个$n\times k$的矩阵$\boldsymbol{R}_1,\boldsymbol{R}_2$，然后
\begin{equation}\boldsymbol{B}=\boldsymbol{R}_1\boldsymbol{R}_2^{\top} \end{equation}

混合模式 #

到目前为止，连同标准的自注意力，我们有5种不同的生成矩阵$\boldsymbol{B}$的方案，它们也可以混合起来，即
\begin{equation}\boldsymbol{B}=\sum_{i=1}^N \alpha_i \boldsymbol{B}_i\end{equation}
其中$\boldsymbol{B}_i$是不同形式的自注意力矩阵，而$\sum\limits_{i=1}^N \alpha_i=1$是可学习参数。

结果分析 #

前面介绍了统称为Synthesizer的几种新型自注意力形式，它们的共同特点是没有保持“token对token”形式，尤其是Random，则完全抛弃了原有注意力的动态特点，变成了静态的矩阵。

那么，这些新型自注意力的效果如何呢？它们又怎样冲击我们对自注意力机制的认识呢？

机器翻译 #

第一个评测任务是机器翻译，详细地比较了各种自注意力形式的效果：

Synthesizer在机器翻译任务上的表现对比

不知道读者怎么想，反正Synthesizer的这些结果是冲击了笔者对自注意力的认知的。表格显示，除了固定的Random外，所有的自注意力形式表现基本上都差不多，而且就算是固定的Random也有看得过去的效果，这表明我们以往对自注意力的认知和解释都太过片面了，并没有揭示自注意力生效的真正原因。

摘要对话 #

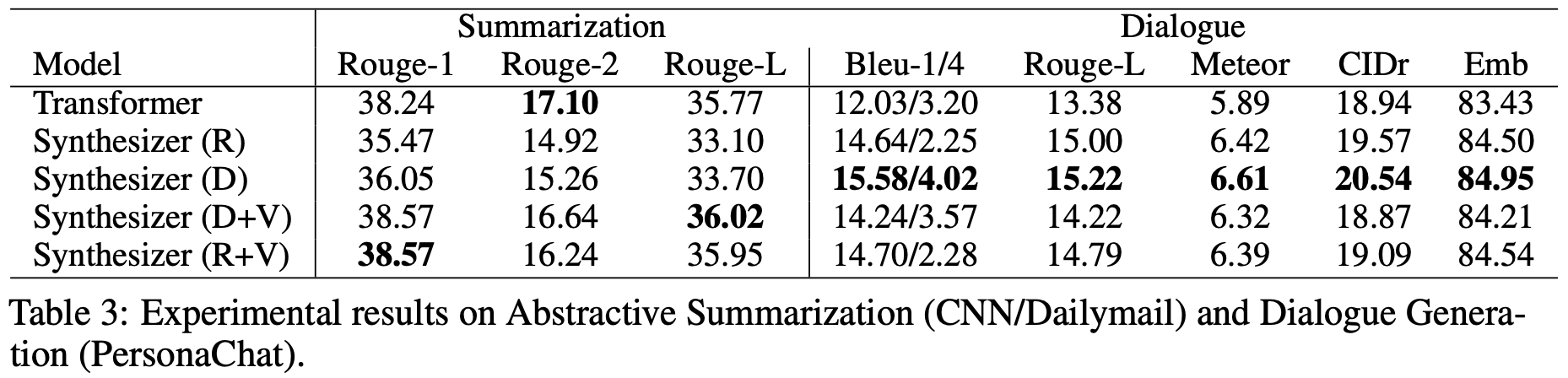
接下来在摘要和对话生成任务上的结果：

Synthesizer在摘要和对话任务上的表现对比

在自动摘要这个任务上，标准注意力效果比较好，但是对话生成这个任务上，结果则反过来：标准的自注意力是最差的，Dense（D）和Random（R）是最好的，而当Dense和Random混合了标准的自注意力后（即 D+V 和 R+V），效果也变差了。这说明标准注意力并没有什么“独占鳌头”的优势，而几个Synthesizer看起来是标准注意力的“退化”，但事实上它们互不从属，各有优势。

预训练+微调 #

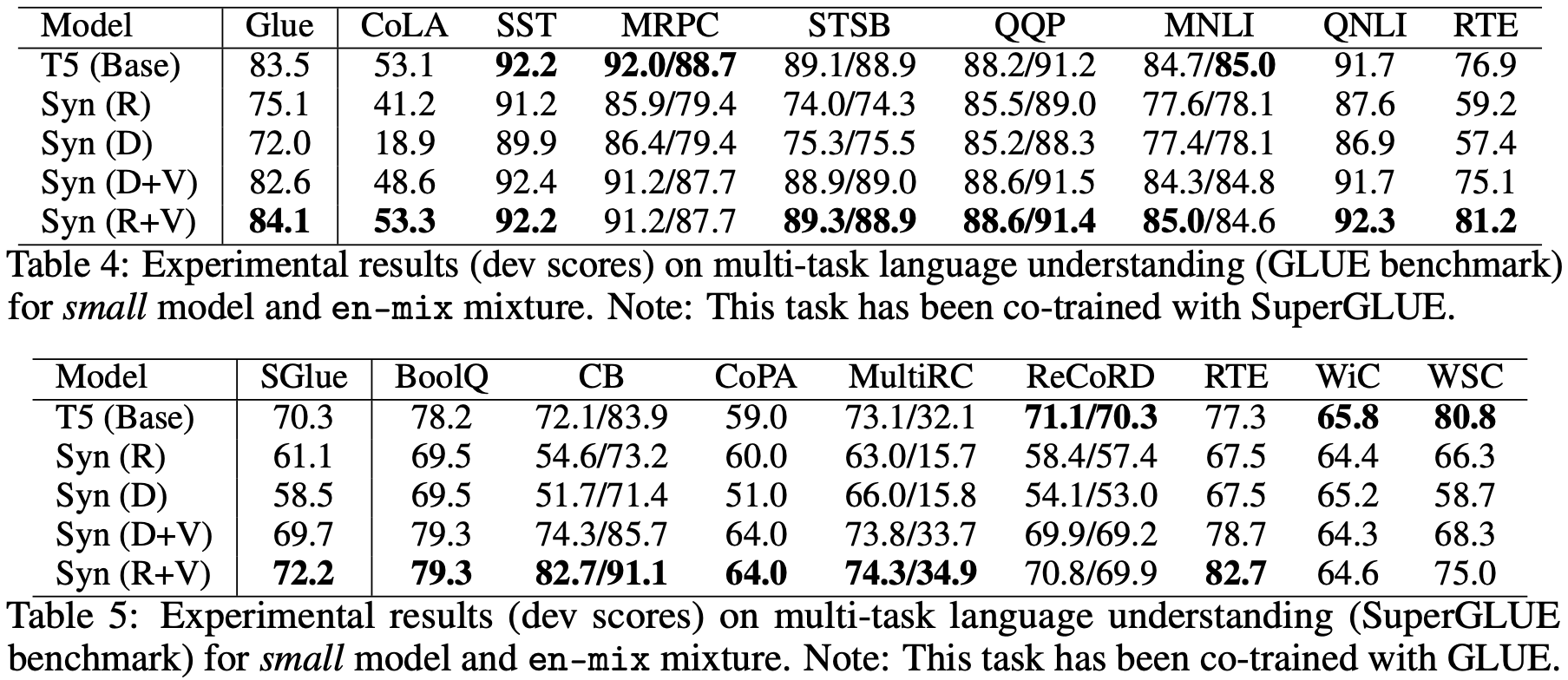
最后，对于我们这些普通读者来说，可能比较关心是“预训练+微调”的效果怎样，也就是说，将BERT之类的模型的自注意力替换之后表现如何？原论文确实也做了这个实验，不过Baseline不是BERT而是T5，结果如下：

Synthesizer在“预训练+微调”的表现对比

在这个结果中，相比标准自注意力，Dense和Random就显得逊色了，这表明Dense和Random也许会在单一任务上表现得比较好，而迁移能力则比较弱。但是不能否定的是，像Random这样的自注意力，由于直接省去了$\boldsymbol{Q}\boldsymbol{K}^{\top}$这个矩阵运算，因此计算效率会有明显提升，因此如果能想法子解决这个迁移性问题，说不准Transformer模型家族将会迎来大换血。

文末小结 #

本文介绍了Google的新工作Synthesizer，它是对目前流行的自注意力机制的反思和探索。论文中提出了几种新型的自注意力机制，并做了相当充分的实验，而实验结果很可能会冲击我们对自注意力机制的已有认知，值得大家读读～

转载到请包括本文地址：https://spaces.ac.cn/archives/7430

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。