数独的自动推理

写在前面：作为离散数学的实验作业，我选择了研究数独。经过测试发现，数独的自动推理还不算难，我把两种常规的推理思路转化为了计算机代码，并结合了随机性推导，得到了一个解题能力还不错的数独程序。事实上，本文的程序还可以进一步优化，以得到更高能力的数独程序（只需要整理一下代码，加上几个循环和判断即可），但是我实在太懒，没有动力继续弄下去了，就这样先和大家分享吧。最后，笔者认为本文的算法是更接近我们的思维的算法。

数独简介 #

历史

相传数独源起于拉丁方阵（Latin Square），1970年代在美国发展，改名为数字拼图（Number Place）、之后流传至日本并发扬光大，以数学智力游戏智力拼图游戏发表。在1984年一本游戏杂志《パズル通信ニコリ》正式把它命名为数独，意思是“在每一格只有一个数字”。后来一位前任香港高等法院的新西兰籍法官高乐德（Wayne Gould）在1997年3月到日本东京旅游时，无意中发现了。他首先在英国的《泰晤士报》上发表，不久其他报纸也发表，很快便风靡全英国，之后他用了6年时间编写了电脑程式，并将它放在网站上，使这个游戏很快在全世界流行。

台湾于2005年5月由“中国时报”首度引进, 且每日连载, 亦造成很大的回响。台湾数独发展协会(Taiwan Sudoku Association, 简称 TSA)亦为世界解谜联盟会员。香港是在2005年7月30日由AM730在创刊时引入数独。中国大陆是在2007年2月28日正式引入数独。北京晚报智力休闲数独俱乐部（数独联盟前身）在新闻大厦举行加入世界谜题联合会的颁证仪式，成为世界谜题联合会的39个成员之一。（引用自“中文维基百科”： http://zh.wikipedia.org/wiki/数独）

规则 #

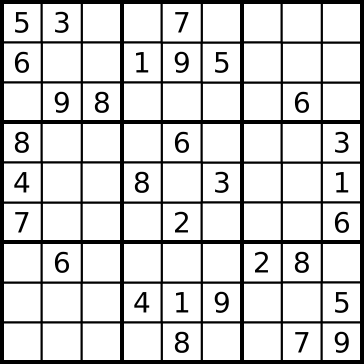
如图1，通常的数独题目都会预先给出一些数字，留下一些空白让我们填满。要求是，每行、每列和每“3$\times$3方块”（图中用粗黑线划分）都必须出现1,2,3,4,5,6,7,8,9这九个阿拉伯数字，左图的答案如右图。

对于一道数独题目，预先给出的数字有多有少，数独难度也有高有低，而且，数独的难度和预先给出的数字数目没有必然联系，甚至对于一个给出的初始数独，正确的答案也可能不止一个。也许正是由于这种不确定性的魅力，才使得数独风靡全球。

推理思路 #

推理的方法无法就是两种，一种是根据前后左右已知的数字确定空白处的数字，实在无法进行确定性推理了，就使用“试探法”，即把一个空白可能的数字列出来，随机选择一个，然后继续进行确定性推理，看看会不会矛盾，如果导致矛盾，就换另外一个数字，重复上面程序。

确定性推导 #

确定性推导基于两种思路，其中第一步都是通过排除法，把所有空白处所有可能的数字列出来，然后分析这些数字列表。比较理想的情况是，某个空白处的可能数字只有一个，那么就相当于确定了这个数字了。比如某列只有2个空白，第一个空白可能的数字是2,9，第二个空白可能的数字是2，那么就确定了第二个空白的数字2。填写了数字2之后，重复这个程序，就确定了第一个空白。

另外一个情况是，每行、每列、每块的所有可能数字中，某个数字只出现了一次，那么就确定了那个数字。比如，某一行有四个空白，第一个空白可能的数字是1,2，第二个空白可能的数字是2,3，第三个空白可能的数字是1,3,4，第四个空白可能的数字是1,2,3，由于4只出现在第三个空白处，而它又必须出现，所以第三个空白处的数字就确定了是4。

随机性推导 #

随机性推导的思路就更加易懂了，在确定性推导实在无法推出更多数字的情况下，我们只能碰运气了。我们找那些只能两个数字可能的空白处，随机选一个填下去，同样来说，多了这个数字后，确定性推导就可以继续进行下去了，如果在进行的过程中发现矛盾，那么就排除这个数字，选择另外一个数字；如果没有矛盾，一般情况下都可以完成整个数独的推导。从某种意义上来说，这也是确定性的推导，只是由于其推导具有一定的随机性，因此冠以“随机性”以表区别。

经过测试，通过以上两个推理，可以完成大部分难度的数独的推算。某些难度比较高的，可以通过再重复上面的程序一次，以得到进一步的结果。（当然，单靠这两种思路，并不总是奏效的（参考下面的测试程序。），由于我们没有使用更进一步的推理或者深度更高的枚举，程序的能力确实不足以尽善尽美。）

计算机实现 #

编程思路 #

下面要做的工作就是把上面的思路翻译成程序代码，本文采用的代码是C++。

为了实现上述思路，我使用了一个9$\times$9的数组B（矩阵）储存已经完成推理的部分结果（用0表示未知的待推导数字），用9$\times$9$\times$9 的数组A （“立方阵”）储存“推理过程”，也就是每个空格可能的数字。A也可以看成每个元素是向量的矩阵，其每个元素的初始值为$(1,2,3,4,5,6,7,8,9)$，即对于任意$i,j$都有$A_{ijk}=k$。每确定一个数字$k$，把与之有关联的（对应的行、列、块）的$A_{ijk}$ 设为0。

程序由主程序和三个函数组成，三个函数分别是确定性推导程序、检测程序、随机性推导程序，分叙如下：

1.确定性推导程序 即把“确定性推导”的推理思路转化为计算机思路，主要用到嵌套循环和判断；

2.检测程序 这是为了配合随机性推导而写的，主要是检测每行、每列以及每块的已知数字中，是否存在重复的非0数字，这是数独正确的必要条件；

3.随机性推导程序 即把“随机性推导”的推理思路转化为计算机思路，主要用到嵌套循环和判断。

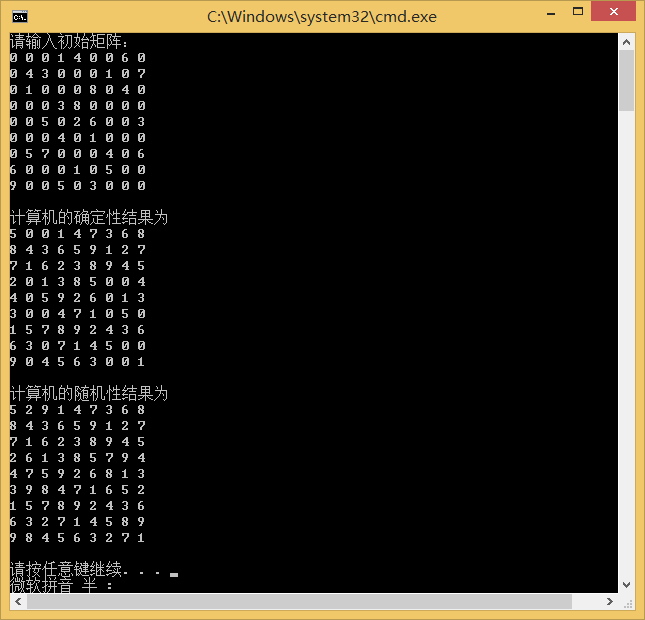
其中，代码和生成的程序放在本文件所在的目录的c++文件夹中（代码在Windows 8 + Visual Studio 2013下编译通过）。下面展示几个推导案例，数独由“数独博士”自动生成。

程序测试 #

入门级测试 #

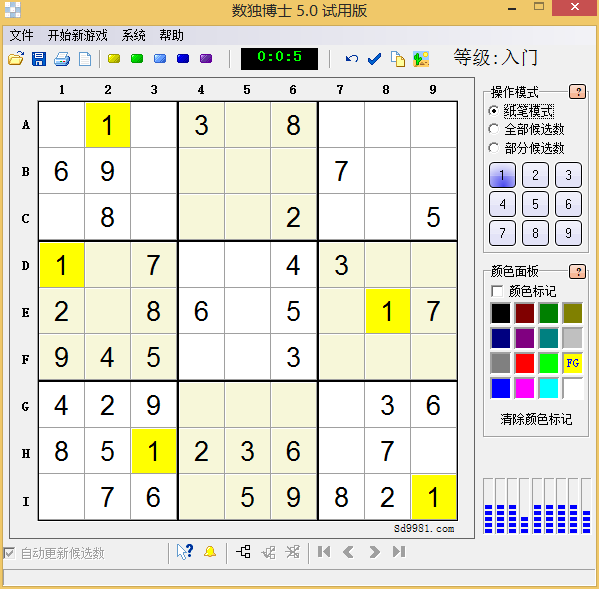
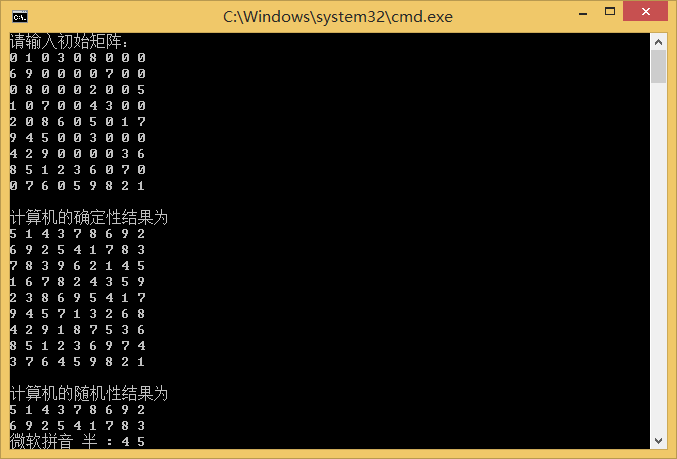
笔者的程序的求解（入门级）

可见，入门级数独仅需确定性搜索就可以完成。这大概也是入门级的“入门”意义所在吧。

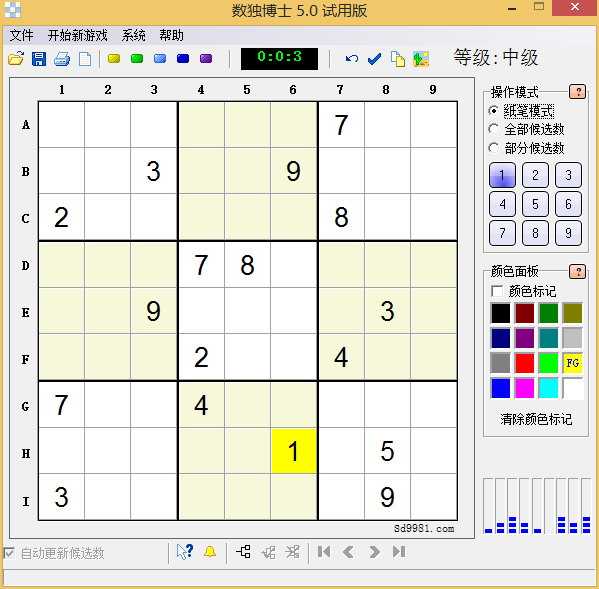
中级测试 #

以上是由数独博士生成的中级数独，但是很遗憾，本程序却解决不了这个数独，原因在于该数独初始数字太少，对于人工来说，可能是自由度较高显得比较简单，但是对于计算机推理来说，这种自由度往往造成了推理上的困难。当然，可以改进本文所用的判断解决这个数独（使用多重“确定+随机”搜索和判断），但是这将会导致程序代码长度激增，因此不再赘述。

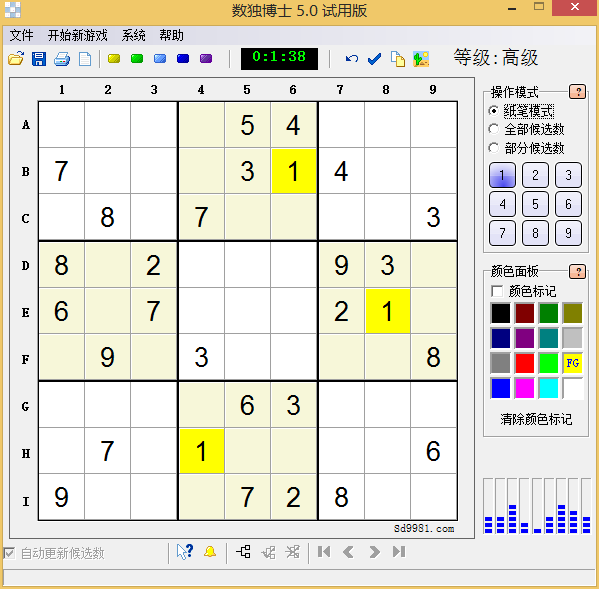
高级测试 #

以上是由数独博士生成的高级数独，使用笔者的程序迭代三次就可以得出最终答案。要注意的是，由于迭代中并没有使用关联判断，因此换个例子就不一定迭代成功了。

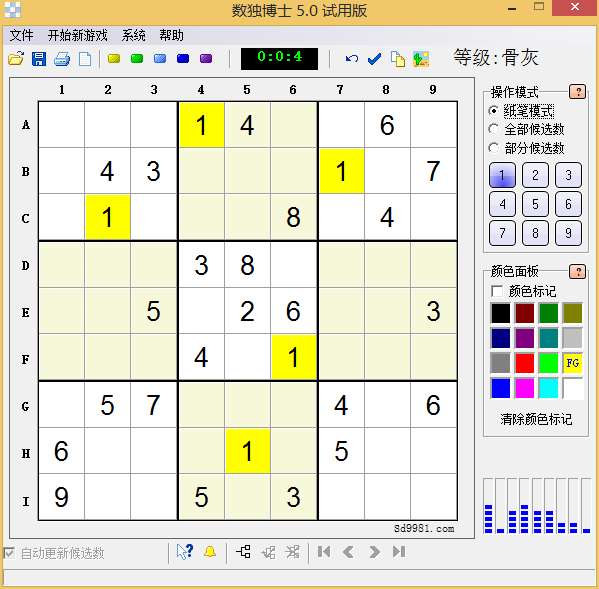
骨灰级测试 #

“骨灰级”意味着“发烧”到了最高境界，意思是难度最高的数独级别。意外的是，测试一个由“数独博士”生成的骨灰级数独，却只需要一次确定性和随机性推导即可。由此可见，本文的算法推导思路跟数独博士的思路并不一致。个人认为本程序的算法更接近人工思维。

最后 #

源码和程序下载：数独推导_苏剑林.zip

转载到请包括本文地址：https://spaces.ac.cn/archives/2527

更详细的转载事宜请参考：《科学空间FAQ》