训练集、验证集和测试集的意义
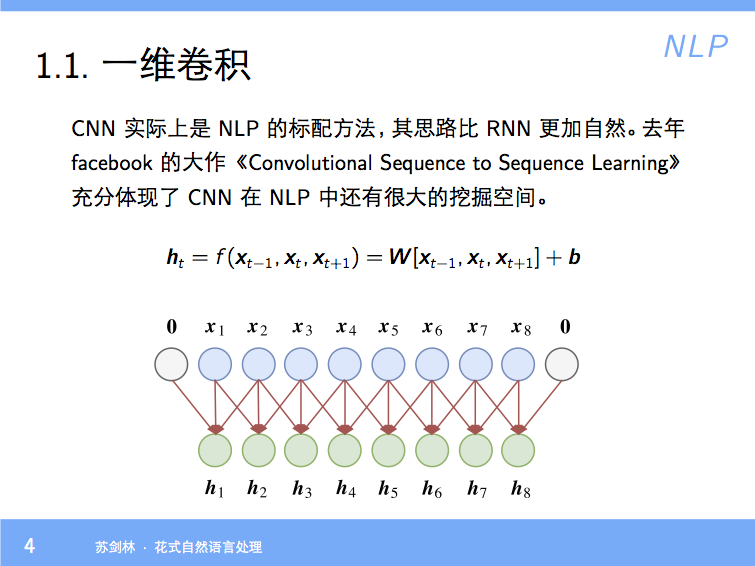
By 苏剑林 | 2017-10-14 | 55060位读者 | 引用分享一个slide:花式自然语言处理
By 苏剑林 | 2018-01-23 | 89326位读者 | 引用【分享】千万级百度知道语料
By 苏剑林 | 2018-01-30 | 90465位读者 | 引用发布
2018年01月30日
数目
共1千万条
格式
[
{
"url": "http://zhidao.baidu.com/question/565618371557484884.html",
"question": "学文员有哪些专科学校",
"tags": [
"学校",
"专科",
"院校信息"
]
},
{
"url": "http://zhidao.baidu.com/question/2079794100345438428.html",
"question": "网赌和澳门赌有区别吗",
"tags": [
"网络",
"澳门",
"赌博"
]
}
]python简单实现gillespie模拟
By 苏剑林 | 2018-06-07 | 79481位读者 | 引用从SamplePairing到mixup:神奇的正则项
By 苏剑林 | 2018-07-07 | 88717位读者 | 引用SamplePairing和mixup是两种一脉相承的图像数据扩增手段,它们看起来很不合理,而操作则非常简单,但结果却非常漂亮:在多个图像分类任务中都表明它们能提高最终分类模型的精度。
某些读者会困惑于一个问题:为什么如此不合理的数据扩增手段,能得到如此好的效果?而本文则要表明,它们看起来是一种数据扩增方法,事实上它们是对模型的一种正则化方案。正如周星驰的电影《国产凌凌漆》的一句经典台词:
表面上看这是一个吹风机,其实它是一个刮胡刀。
数据扩增
让我们从数据扩增说起。数据扩增是指我们在对原始数据做一些简单的变换后,它们对应的类别往往不会变化,所以我们可以在原来数据的基础上,“造”出更多的数据来。比如一幅小狗的照片,将它水平翻转、轻微的旋转、裁剪、平移等操作后,我们认为它的类别没有变化,它还是原来的那只狗。这样一来,从一个样本我们可以衍生出好几个样本,从而增加了训练样本量。
又一道川菜!媲美“开水白菜”的瓜燕穗肚
By 苏剑林 | 2018-11-15 | 37121位读者 | 引用分享:用LaTeX+MathJax画一个三维三阶环方
By 苏剑林 | 2019-03-28 | 20337位读者 | 引用昨天看到数学研发论坛在讨论三维三阶幻方,论坛里的各大牛都已经讨论得差不多了,我也没什么好插话的。然后突发奇想,能不能用纯LaTeX画出一个这样的立体幻方出来?
昨天下午折腾了好一会儿,最后只抛出了个半成品,然后经过论坛的mathe大佬继续完善后,终于成功地画出来了:
\begin{array}{ccccccccccc}
& & & & 4 & —& —& — & — & 25 & —& —& — & — & 11
\\
& & & \require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & && &\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} && &&\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &|
\\
& & 14 & — & — & —& — & 22 & — & — & — & —& 7 & & |
\\
& \require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}& &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & &\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}&&\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & | & & | \\
24 & — & —& —& — & 1 & —& —& — & — & 18 & & | & & |\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & &\color{red}{13} &| & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} &\color{red}{27} & | & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & | &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&5\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & \require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & | & & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &| & & |&\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} &|\\
|& & \color{red}{8} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& | &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \color{red}{12} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& | &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&22&&|\\
|&\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & | &\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}& | &\require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|} & | &&|\\
15 & — & —& —& — & 3 & — & — & —& —& 21 & & | & &|\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & & \color{red}{9} &| &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \color{red}{26} &|&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&|&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&6\\
|& & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}}&\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} & &| & &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\vdots}} &\require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &&|&&|&\style{display: inline-block; transform: rotate(45deg)}{|}\\
|& &\color{red}{16} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}} &|&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& \color{red}{8} &\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&\require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}& | & \require{HTML} \style{display: inline-block; opacity:0.5;}{\color{red}{\cdots}}&17\\
|& \require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}}& & & &|& \require{HTML} \style{display: inline-block; transform: rotate(45deg); opacity:0.5;}{\color{red}{\vdots}} &&&& | & \require{HTML} \style{display: inline-block; transform: rotate(45deg)}{|}\\
23 & — & — & — & — & 2 & — & — & — & — & 19\\
\end{array}
事实上代码里边还内嵌了一些HTML代码,所以不算是严格的纯LaTeX代码,应该说是LaTeX+MathJax的结合。
简述无偏估计和有偏估计
By 苏剑林 | 2019-06-19 | 90579位读者 | 引用对于大多数读者(包括笔者)来说,他们接触到的第一个有偏估计量,应该是方差
\begin{equation}\hat{\sigma}^2_{\text{有偏}} = \frac{1}{n}\sum_{i=1}^n \left(x_i - \hat{\mu}\right)^2,\quad \hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i\label{eq:youpianfangcha}\end{equation}
然后又了解到对应的无偏估计应该是
\begin{equation}\hat{\sigma}^2_{\text{无偏}} = \frac{1}{n-1}\sum_{i=1}^n \left(x_i - \hat{\mu}\right)^2\label{eq:wupianfangcha}\end{equation}
在很多人的眼里,公式\eqref{eq:youpianfangcha}才是合理的,怎么就有偏了?公式\eqref{eq:wupianfangcha}将n换成反直觉的n-1,反而就无偏了?
下面试图用尽量清晰的语言讨论一下无偏估计和有偏估计两个概念。











最近评论