科学空间|Scientific Spaces

自从GPT、BERT等预训练模型流行起来后，其中一个明显的趋势是模型越做越大，因为更大的模型配合更充分的预训练通常能更有效地刷榜。不过，理想可以无限远，现实通常很局促，有时候模型太大了，大到哪怕你拥有了大显存的GPU甚至TPU，依然会感到很绝望。比如GPT2最大的版本有15亿参数，最大版本的T5模型参数量甚至去到了110亿，这等规模的模型，哪怕在TPU集群上也没法跑到多大的batch size。

这时候通常要往优化过程着手，比如使用混合精度训练（tensorflow下还可以使用一种叫做bfloat16的新型浮点格式），即省显存又加速训练；又或者使用更省显存的优化器，比如RMSProp就比Adam更省显存。本文则介绍AdaFactor，一个由Google提出来的新型优化器，首发论文为《Adafactor: Adaptive Learning Rates with Sublinear Memory Cost》。AdaFactor具有自适应学习率的特性，但比RMSProp还要省显存，并且还针对性地解决了Adam的一些缺陷。

Adam

首先我们来回顾一下常用的Adam优化器的更新过程。设$t$为迭代步数，$\alpha_t$为当前学习率，$L(\theta)$是损失函数，$\theta$是待优化参数，$\epsilon$则是防止溢出的小正数，那么Adam的更新过程为

点击阅读全文...

在NLP中，我们经常要去比较两个句子的相似度，其标准方法是想办法将句子编码为固定大小的向量，然后用某种几何距离（欧氏距离、$\cos$距离等）作为相似度。这种方案相对来说比较简单，而且检索起来比较快速，一定程度上能满足工程需求。

此外，还可以直接比较两个变长序列的差异性，比如编辑距离，它通过动态规划找出两个字符串之间的最优映射，然后算不匹配程度；现在我们还有Word2Vec、BERT等工具，可以将文本序列转换为对应的向量序列，所以也可以直接比较这两个向量序列的差异，而不是先将向量序列弄成单个向量。

后一种方案速度相对慢一点，但可以比较得更精细一些，并且理论比较优雅，所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标，分别简称为WMD、WRD。

Earth Mover's Distance

本文要介绍的两个指标都是以Wasserstein距离为基础，这里会先对它做一个简单的介绍，相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”（Earth Mover's Distance，EMD），因为它可以用一个“推土”的例子来通俗地表达它的含义。

点击阅读全文...

众所周知，尽管基于Attention机制的Transformer类模型有着良好的并行性能，但它的空间和时间复杂度都是$\mathcal{O}(n^2)$级别的，$n$是序列长度，所以当$n$比较大时Transformer模型的计算量难以承受。近来，也有不少工作致力于降低Transformer模型的计算量，比如模型剪枝、量化、蒸馏等精简技术，又或者修改Attention结构，使得其复杂度能降低到$\mathcal{O}(n\log n)$甚至$\mathcal{O}(n)$。

前几天笔者读到了论文《Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention》，了解到了线性化Attention（Linear Attention）这个探索点，继而阅读了一些相关文献，有一些不错的收获，最后将自己对线性化Attention的理解汇总在此文中。

Attention

当前最流行的Attention机制当属Scaled-Dot Attention，形式为
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\label{eq:std-att}\end{equation}
这里的$\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$，简单起见我们就没显式地写出Attention的缩放因子了。本文我们主要关心Self Attention场景，所以为了介绍上的方便统一设$\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}\in\mathbb{R}^{n\times d}$，一般场景下都有$n > d$甚至$n\gg d$（BERT base里边$d=64$）。

点击阅读全文...

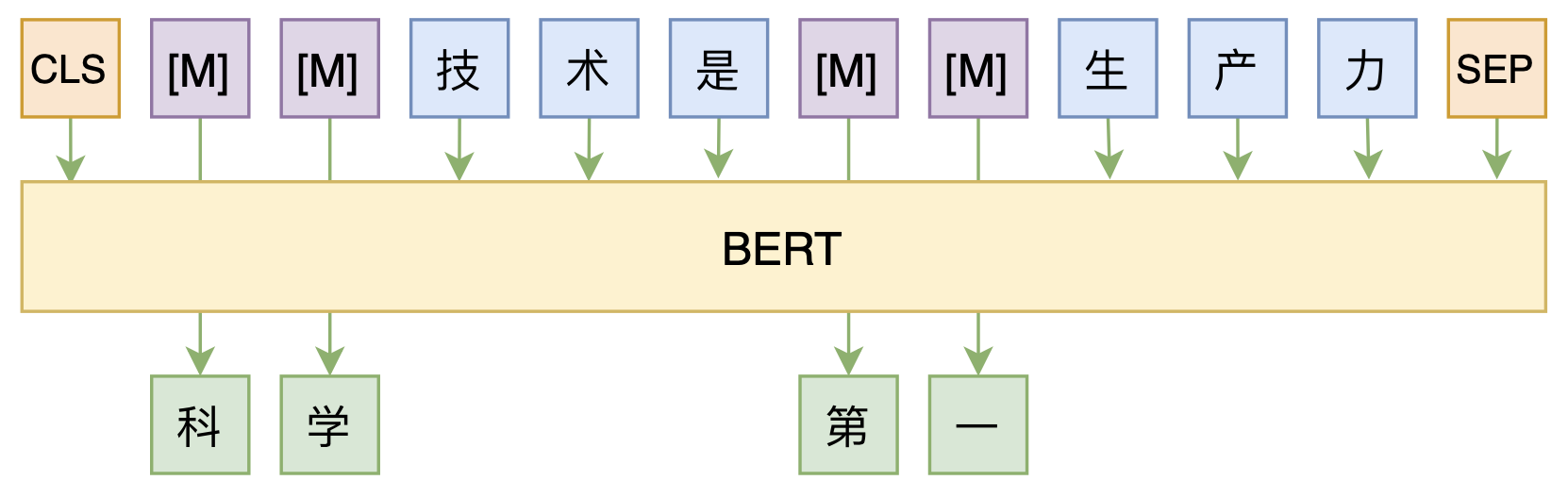
大家都知道，MLM（Masked Language Model）是BERT、RoBERTa的预训练方式，顾名思义，就是mask掉原始序列的一些token，然后让模型去预测这些被mask掉的token。随着研究的深入，大家发现MLM不单单可以作为预训练方式，还能有很丰富的应用价值，比如笔者之前就发现直接加载BERT的MLM权重就可以当作UniLM来做Seq2Seq任务（参考这里），又比如发表在ACL 2020的《Spelling Error Correction with Soft-Masked BERT》将MLM模型用于文本纠错。

MLM任务示意图

然而，仔细读过BERT的论文或者亲自尝试过的读者应该都知道，原始的MLM的训练效率是比较低的，因为每次只能mask掉一小部分的token来训练。ACL 2020的论文《Fast and Accurate Deep Bidirectional Language Representations for Unsupervised Learning》也思考了这个问题，并且提出了一种新的MLM模型设计，能够有更高的训练效率和更好的效果。

点击阅读全文...

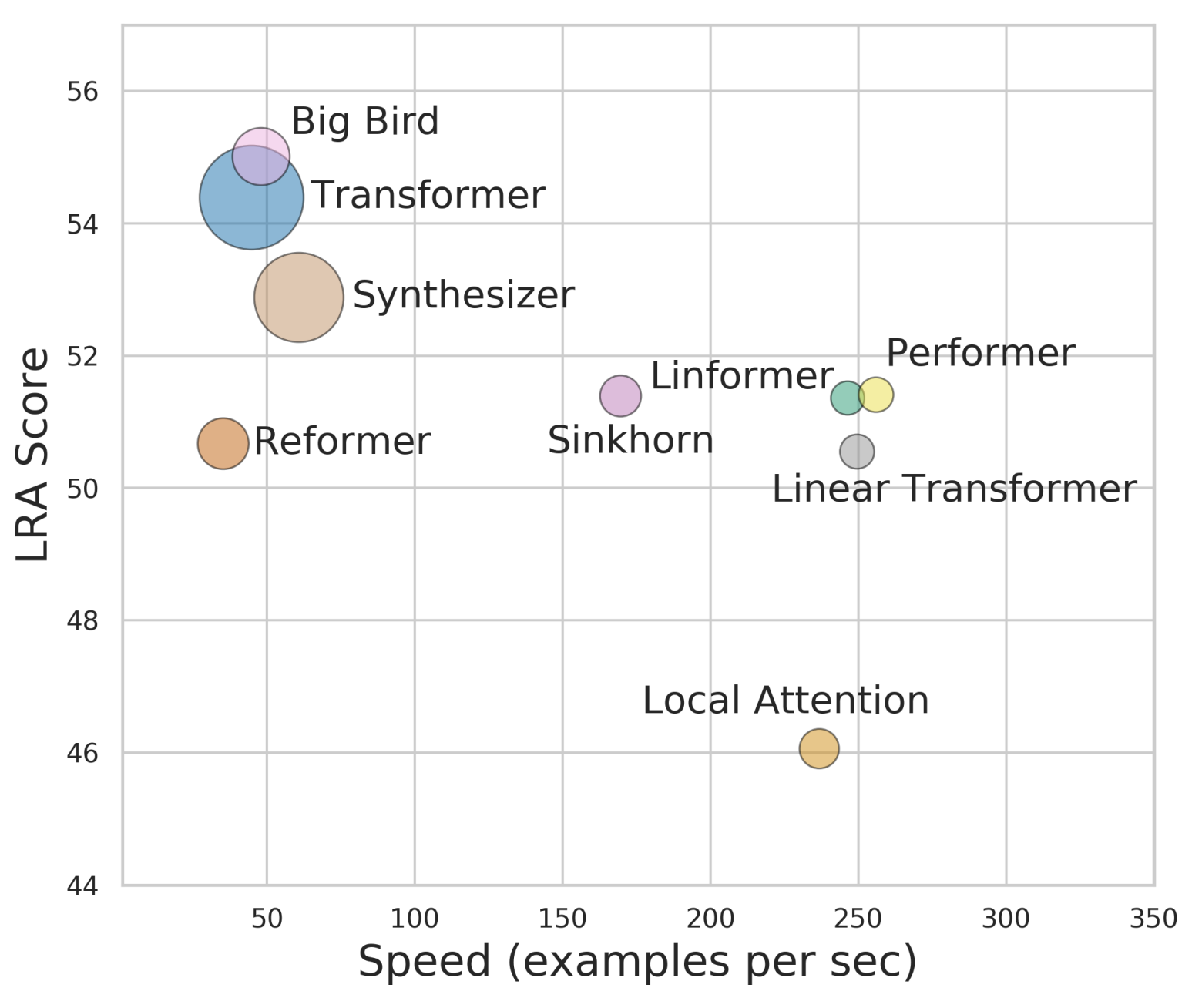
Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了，改变这一复杂度的思路主要有两种：一是走稀疏化的思路，比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird，等等；二是走线性化的思路，这部分工作我们之前总结在《线性Attention的探索：Attention必须有个Softmax吗？》中，读者可以翻看一下。本文则介绍一项新的改进工作Performer，出自Google的文章《Rethinking Attention with Performers》，它的目标相当霸气：通过随机投影，在不损失精度的情况下，将Attention的复杂度线性化。

各个Transformer模型的“效果-速度-显存”图，纵轴是效果，横轴是速度，圆圈的大小代表所需要的显存。理论上来说，越靠近右上方的模型越好，圆圈越小的模型越好

说直接点，就是理想情况下我们可以不用重新训练模型，输出结果也不会有明显变化，但是复杂度降到了$\mathcal{O}(n)$！看起来真的是“天上掉馅饼”般的改进了，真的有这么美好吗？

点击阅读全文...

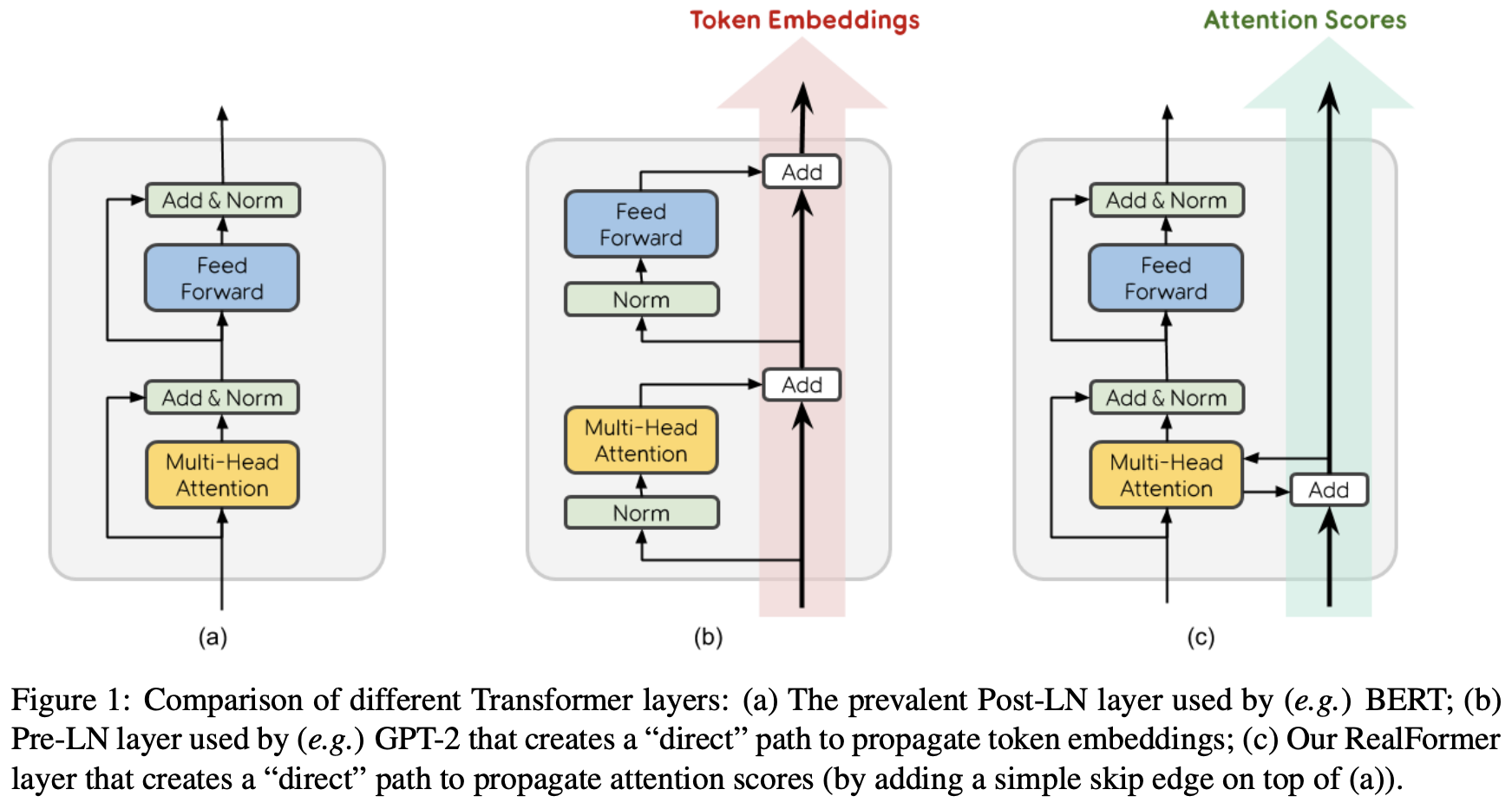
大家知道Layer Normalization是Transformer模型的重要组成之一，它的用法有PostLN和PreLN两种，论文《On Layer Normalization in the Transformer Architecture》中有对两者比较详细的分析。简单来说，就是PreLN对梯度下降更加友好，收敛更快，对训练时的超参数如学习率等更加鲁棒等，反正一切都好但就有一点硬伤：PreLN的性能似乎总略差于PostLN。最近Google的一篇论文《RealFormer: Transformer Likes Residual Attention》提出了RealFormer设计，成功地弥补了这个Gap，使得模型拥有PreLN一样的优化友好性，并且效果比PostLN还好，可谓“鱼与熊掌兼得”了。

PostLN、PreLN和RealFormer结构示意图

点击阅读全文...

不同于RNN、CNN等模型，对于Transformer模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此我们大体有两个选择：1、想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；2、想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。

虽然说起来主要就是绝对位置编码和相对位置编码两大类，但每一类其实又能衍生出各种各样的变种，为此研究人员可算是煞费苦心、绞尽脑汁了，此外还有一些不按套路出牌的位置编码。本文就让我们来欣赏一下研究人员为了更好地表达位置信息所构建出来的“八仙过海，各显神通”般的编码方案。

绝对位置编码

形式上来看，绝对位置编码是相对简单的一种方案，但即便如此，也不妨碍各路研究人员的奇思妙想，也有不少的变种。一般来说，绝对位置编码会加到输入中：在输入的第$k$个向量$\boldsymbol{x}_k$中加入位置向量$\boldsymbol{p}_k$变为$\boldsymbol{x}_k + \boldsymbol{p}_k$，其中$\boldsymbol{p}_k$只依赖于位置编号$k$。

点击阅读全文...

最近笔者做了一些理解和改进Transformer的尝试，得到了一些似乎还有价值的经验和结论，遂开一个专题总结一下，命名为“Transformer升级之路”，既代表理解上的深入，也代表结果上的改进。

作为该专题的第一篇文章，笔者将会介绍自己对Google在《Attention is All You Need》中提出来的Sinusoidal位置编码
\begin{equation}\left\{\begin{aligned}&\boldsymbol{p}_{k,2i}=\sin\Big(k/10000^{2i/d}\Big)\\
&\boldsymbol{p}_{k, 2i+1}=\cos\Big(k/10000^{2i/d}\Big)
\end{aligned}\right.\label{eq:sin}\end{equation}
的新理解，其中$\boldsymbol{p}_{k,2i},\boldsymbol{p}_{k,2i+1}$分别是位置$k$的编码向量的第$2i,2i+1$个分量，$d$是向量维度。

作为位置编码的一个显式解，Google在原论文中对它的描述却寥寥无几，只是简单提及了它可以表达相对位置信息，后来知乎等平台上也出现了一些解读，它的一些特点也逐步为大家所知，但总体而言比较零散。特别是对于“它是怎么想出来的”、“非得要这个形式不可吗”等原理性问题，还没有比较好的答案。

因此，本文主要围绕这些问题展开思考，可能在思考过程中读者会有跟笔者一样的感觉，即越思考越觉得这个设计之精妙漂亮，让人叹服～

点击阅读全文...