科学空间|Scientific Spaces

这也是我的期末论文之一...全文共17页，包括了四元数的构造方法，初等应用等。附录包括行列式与体积、三维旋转的描述等。使用LaTex进行写作（LaTex会让你爱上数学写作的）

几何的数与数的几何
――超复数的浅探究

摘要
今天，不论是数学还是物理的高维问题，都采用向量分析为基本工具，数学物理中难觅四元数的影子。然而在历史上，四元数的发展有着重要的意义。四元数（Quaternion）运算实际上是向量分析的“鼻祖”，向量点积和叉积的概念也首先出现在四元数的运算中，四元数的诞生还标记着非交换代数的开端。即使是现在，四元数还是计算机描述三维空间旋转问题最简单的工具。另外，作为复数的推广，四元数还为某些复数问题的一般化提供了思路。

本文把矩阵与几何适当地结合起来，利用矩阵行列式$\det (AB) =(\det A)(\det B)$这一性质得出了四元数以及更高维的超复数的生成规律，并讨论了它的一些性质以及它在描述旋转方面的应用。部分证明细节和不完善的思想放到了附录之中。

点击阅读全文...

在上一篇文章中，我们得到了一维弹簧运动的方程
$$m\frac{\partial^2 X}{\partial t^2}=k\frac{\partial^2 X}{\partial \xi^2}$$
并且得到了通解
$$X=F(u)+H(v)=F(\xi+\beta t)+H(\xi-\beta t)$$
或者
$$X(\xi,t)=\frac{1}{2}\left[X_0(\xi+\beta t)+X_0(\xi-\beta t)\right]+\frac{1}{2\beta}\int_{\xi-\beta t}^{\xi+\beta t} X_1 (s)ds$$
在文章的末尾，提到过这个解是有些问题的。现在让我们来详细分析它。

点击阅读全文...

这一周科学空间时断时续的，原因是原来的服务器两个内存条坏了，内存不够用。

后来天文台决定给我们换一台服务器，这两天主要在转移数据，从而不能访问。

目前，基本上已经转移好了，服务器升级工作基本完成。新服务器的升级，CPU从原来的8核升级为48核，内存从16GB升级为64GB。再次感谢国家天文台宇宙驿站给予我们的服务^_^感谢各位技术人员的努力，让我们一起把中文科普事业做得更好~

元宵节快乐

今天是2014年2月14日，农历正月十五，传统的元宵佳节，祝大家元宵节快乐！

不过虽说是元宵佳节，但是我们这里的习俗却没有闹元宵的，好像在我们这里元宵节就像普通的初一十五一样，惯例地上个香，祭下神而已，唯一特别的地方就是早上妈妈放了个鞭炮，什么汤圆、灯笼、灯谜都没有呢。不过这并不妨碍我欣赏元宵节，印象里好像上学以来这是第一次在家过元宵节。幸好没有参加美国数学建模，不然又少了半个月的假期，少了一次难得的元宵，而多了得不偿失的劳动...

今天也是西方的情人节，但在这里我只强调元宵节。首要原因却不是我目前单身（当然这也是原因之一^_^），而是元宵节是中国传统节日。我这个人有个奇怪的“嗜好”，反正越潮流的东西我越不跟。于是乎，既然那么多人都庆祝着西方节日（什么万圣节、圣诞节、情人节），那么我就偏不凑这个热闹。我又想起了去年圣诞前夕有个师弟过来向我们宣传和推销圣诞的东西，被我批了一顿，我直言说“你为什么不等元旦再来？”。我想，如果哪一天，我也有机会庆祝情人节，我也只是庆祝中国的情人节，总感觉中国的情人节美多了：七夕，Qixi Festival，多美！不论是典故还是习俗都更美~

点击阅读全文...

为了形象地展示为什么有些系统需要旋转720度而不是360度才能恢复原状，费曼想到了一个“茶杯法”。看了“茶杯法”的步骤之后，我突然想起了电影《太极1》的梁小龙的一个端药镜头，正好对应着费曼的“茶杯法”，遂把镜头剪了出来，供大家欣赏。

请仔细观察梁小龙的手转了多少圈？

点击阅读全文...

进入期末了，很多同学都开始复习了，这学期我选的几门课到现在还不是很熟悉，本想也在趁着这段时间好好看看。偏生五天前我在浏览数学研发论坛的编程擂台时看到了这样的一道题目：

设对于给定的$L$，方程
$$\frac{1}{x}+\frac{1}{y}=\frac{1}{n}$$
满足$0 < x < y \leq L$的正整数解共有$f(L)$种情况。比如$f(6)=1,f(12)=3,f(1000)=1069$，求$f(10^{12})$。

这道题目的来源是Project Euler的第454题：Diophantine reciprocals III（丢潘图倒数方程），题目简短易懂，但又不失深度，正符合我对理想题目的定义。而且最近在学习Python学习得不亦乐乎，看到这道题目就跃跃欲试。于是乎，我的五天时间就没有了，而且过程中几乎耗尽了我现在懂的所有编程技巧。由于不断地测试运行，我的电脑发热量比平时大了几倍，真是辛苦了我的电脑。最后的代码，自我感觉已经是我目前写的最精彩的代码了。在此与大家共享和共勉~

上述表达式是分式，不利于编程，由于$n=\frac{xy}{x+y}$，于是上述题目也等价于求$(x+y)|xy$（意思是$x+y$整除$xy$）的整数解。

点击阅读全文...

在查找量子化有关资料的时候，笔者查找到了一系列名为《漫谈几何量子化》的文章，并进一步查询得知，作者为季候风，原来发表在繁星客栈（顺便提一下，繁星客栈是最早的理论物理论坛之一，现在已经不能发帖了，但是上面很多资料都弥足珍贵），据说这是除正则量子化和路径积分量子化外的第三种量子化方法。网上鲜有几何量子化的资料，更不用说是中文资料了，于是季候风前辈的这一十五篇文章便显得格外有意义了。

然而，虽然不少网站都转载了这系列文章，但是无一例外地，文章中的公式图片已经失效了，后来笔者在百度网盘那找到其中的十四篇pdf格式的（估计是网友在公式图片失效前保存下来的），笔者通过替换公式服务器的方式找回了第十五篇，把第十五篇也补充进去了。（见漫谈几何量子化（原文档）.zip）

虽然这样已经面前能够阅读了，但是总感觉美中不足，虽然笔者花了三天时间把文章重新用$\LaTeX$录入了，主要是把公式重新录入了，简单地排版了一下。现放出来与大家分享。

点击阅读全文...

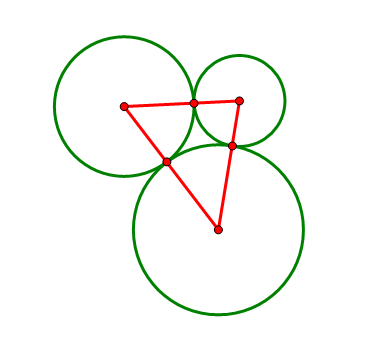
在学车的时候，我堂大哥曾问我一道作圆的问题：

三圆的外切圆和内切圆 (1)

平面上给出三个两两相切的圆以及它们的圆心，求作一个圆与这三个圆都相切（尺规作图）。

如果从纯几何的途径入手，我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目，于是很快想到一个名词：反演。反演可以将圆反演成直线（圆过反演点），也可以将圆反演成圆（圆不过反演点），而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演，就变回原来的图形。本题的难点在于圆太多，利用反演，我们可以将它变为两条直线和一个圆的问题。

假设读者已经有了反演的基本知识，如果没有，请到
http://zh.wikipedia.org/wiki/反演

阅读相关内容。

点击阅读全文...