FLASH:可能是近来最有意思的高效Transformer设计
By 苏剑林 | 2022-02-25 | 283764位读者 |高效Transformer,泛指所有概率Transformer效率的工作,笔者算是关注得比较早了,最早的博客可以追溯到2019年的《为节约而生:从标准Attention到稀疏Attention》,当时做这块的工作很少。后来,这类工作逐渐多了,笔者也跟进了一些,比如线性Attention、Performer、Nyströmformer,甚至自己也做了一些探索,比如之前的“Transformer升级之路”。再后来,相关工作越来越多,但大多都很无趣,所以笔者就没怎么关注了。
大抵是“久旱逢甘霖”的感觉,最近终于出现了一个比较有意思的高效Transformer工作——来自Google的《Transformer Quality in Linear Time》,经过细读之后,笔者认为论文里边真算得上是“惊喜满满”了~
何喜之有 #
什么样的结果值得我们用“惊喜”来形容?有没有言过其实?我们不妨先来看看论文做到了什么:
1、提出了一种新的Transformer变体,它依然具有二次的复杂度,但是相比标准的Transformer,它有着更快的速度、更低的显存占用以及更好的效果;
2、提出一种新的线性化Transformer方案,它不但提升了原有线性Attention的效果,还保持了做Decoder的可能性,并且做Decoder时还能保持高效的训练并行性。
说实话,笔者觉得做到以上任意一点都是非常难得的,而这篇论文一下子做到了两点,所以我愿意用“惊喜满满”来形容它。更重要的是,论文的改进总的来说还是比较自然和优雅的,不像很多类似工作一样显得很生硬。此外,笔者自己也做了简单的复现实验,结果显示论文的可复现性应该是蛮好的,所以真的有种“Transformer危矣”的感觉了。
门控注意 #
闲话少说,进入主题。我们知道标准的Transformer其实是Attention层和FFN层交替构建的,而这篇论文的核心是提出了一个融合了两者的新设计GAU(Gated Attention Unit,门控注意力单元),它是新模型更快、更省、更好的关键,此外它使得整个模型只有一种层,也显得更为优雅。
威力初显 #
怎么做到Attention和FFN的融合呢?首先,标准的FFN是两层MLP模型:
\begin{equation}\boldsymbol{O}=\phi(\boldsymbol{X}\boldsymbol{W}_u)\boldsymbol{W}_o\end{equation}
这里$\boldsymbol{X}\in\mathbb{R}^{n\times d},\boldsymbol{W}_u\in\mathbb{R}^{d\times e},\boldsymbol{W}_o\in\mathbb{R}^{e\times d}$而$\phi$是激活函数。后来,《GLU Variants Improve Transformer》发现使用了GLU(Gated Linear Unit,门控线性单元)的FFN效果更好,并为后来的mT5所用,其形式为:
\begin{equation}\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{V})\boldsymbol{W}_o,\quad \boldsymbol{U}=\phi_u(\boldsymbol{X}\boldsymbol{W}_u),\quad\boldsymbol{V}=\phi_v(\boldsymbol{X}\boldsymbol{W}_v)\end{equation}
这里$\boldsymbol{W}_u,\boldsymbol{W}_v\in\mathbb{R}^{d\times e}$而$\odot$是逐位对应相乘(Hadamard积)。GLU更有效并不是一件让人意外的事情,早在2017年Facebook的《Convolutional Sequence to Sequence Learning》中GLU就起到了关键作用,此外笔者之前研究的DGCNN也肯定了GLU的有效性。
一般情况下的GLU是$\boldsymbol{U}$不加激活函数而$\boldsymbol{V}$加Sigmoid,但这篇论文$\boldsymbol{U},\boldsymbol{V}$都加了激活函数Swish(也叫SiLU,Sigmoid Linear Unit),这可以在附录中的源码找到,此处跟主流GLU用法略有不同,特别指出一下。
强强联合 #
既然GLU式的FFN更有效,那么我们就以它为基础进行修改。注意到FFN不能取代Attention,是因为它的各个token之间没有进行交互,也就是矩阵$\boldsymbol{U},\boldsymbol{V}$的每一行都是独立运算的。为了补充这点不足,一个自然的想法就是把token之间的联系补充到$\boldsymbol{U},\boldsymbol{V}$上去,而为了体现出跟Attetion的结合,那么一个比较自然的设计就是
\begin{equation}\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{A}\boldsymbol{V})\boldsymbol{W}_o\label{eq:mix}\end{equation}
其中$\boldsymbol{A}\in\mathbb{R}^{n\times n}$是Attention矩阵,它负责融合token之间的信息。这样出来的$\boldsymbol{O}$就包含了token之间的交互,原则上它可以取代Attention。至于$\boldsymbol{A}$怎么算,我们等会再说。
在式$\eqref{eq:mix}$中,如果$\boldsymbol{A}$等于单位阵$\boldsymbol{I}$,那么它就是GLU式的FFN;而如果$\boldsymbol{U}$是全1矩阵,那么它就是普通的注意力机制。所以说,$\eqref{eq:mix}$是Attention和FFN的一个简单而自然的融合,我们期望它能同时替换掉Attention和FFN,甚至有更好的表现。
弱注意力 #
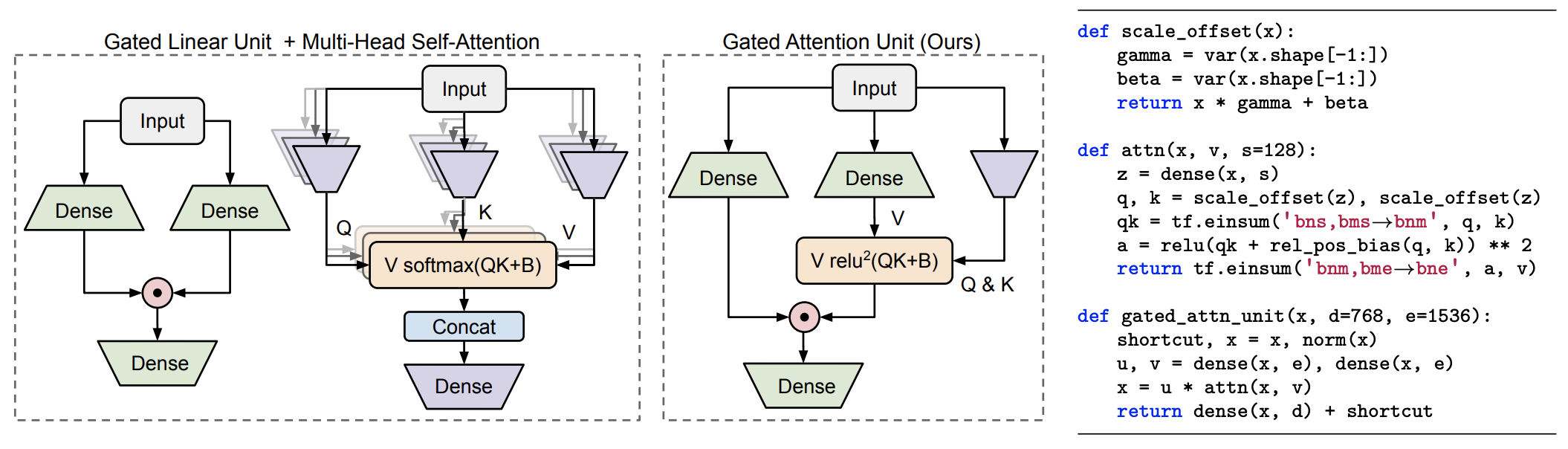
刚才说了,GLU本身就很强,不然Facebook也无法凭借CNN+GLU做到了当时Seq2Seq的SOTA,而既然GLU那么强,那么一个猜测是它会弱化对Attention的依赖。也就是说,虽然在式$\eqref{eq:mix}$中$\boldsymbol{A}$是不可或缺的,但或许我们可以简化它的形式。事实上确实如此,原论文使用了如下的简化版Attention矩阵:
\begin{equation}\boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right),\quad \boldsymbol{Z}=\phi_z(\boldsymbol{X}\boldsymbol{W}_z)\label{eq:relu-att}\end{equation}
这里$\boldsymbol{W}_z\in\mathbb{R}^{d\times s}$,$s$即注意力的head_size,文中取了$s=128$,而$\mathcal{Q},\mathcal{K}$是简单的仿射变换(像Layer Norm中的乘$\gamma$加$\beta$),$\text{relu}^2$则是$\text{relu}$后再平方。
跟标准的Scaled-Dot Self Attention类似,这里的注意力矩阵还是$\boldsymbol{Q},\boldsymbol{K}$的内积并除以维度的平方根而来,复杂度还是$\mathcal{O}(n^2)$的,不同的是这里简化了$\boldsymbol{Q},\boldsymbol{K}$的来源变换,并且激活函数换用了$\text{relu}^2$。大家可能对这个激活函数比较陌生,事实上这是作者团队在他们之前的论文《Primer: Searching for Efficient Transformers for Language Modeling》用NAS的方式搜出来的。最后的$1/n$是简单的归一化因子,用以消除长度的影响。这个设计的成功也表明,注意力机制中的softmax不是必须的,可以换成常规的激活函数加简单的归一化。
注意,按照论文附录的参考代码,原论文化简后的缩放因子实际上是$\frac{1}{n^2}$而不是上式的$\frac{1}{ns}$,笔者认为$\frac{1}{ns}$会更加合理一些,不然当$n$足够大时,每一项注意力都过小了。况且对照标准注意力所用的softmax,其分母也只是$\mathcal{O}(n)$的量级而已,设成$n^2$实在感觉不科学。笔者也简单做过对比实现,发现在512长度下$\frac{1}{ns}$版本还轻微好点,所以这里就按笔者的直觉来介绍了。
以一当十 #
接下来请各位看官不要眨眼了,真正的“重磅”要登场了!可能GLU真的太强了,它对Attention的依赖真的非常非常弱,以至于作者们发现:只用一个头就够了!
我们知道标准的Transformer用的是多头注意力机制,在运算过程中需要产生$bhn^2$大小的矩阵,$b$是batch_size而$h$是头数,试想一下,当$n=1000$、$n=2000$甚至更大时,$n^2$已经够“惨”的了,还要活生生地乘个$h$,不管对时间还是空间复杂度无疑都是“雪上加霜”。而如今,只要一个头的GAU,就可以达到相同甚至更好的效果,不仅提高了计算速度,还降低了显存占用量,几乎算得上是“免费的午餐”了。
当GAU只有一个头时,$\boldsymbol{W}_z$的参数量就很少了,主要参数量在$\boldsymbol{W}_u,\boldsymbol{W}_v,\boldsymbol{W}_o$上,所以GAU的参数量大约为$3de$;而在标准的Transformer中,Attention的参数量为$4d^2$,FFN的参数量为$8d^2$(标准FFN中一般是$e=4d$),所以总参数量为$12d^2$。因此,从参数量看,当$e=2d$时,两层GAU大致上就等于原来的Attention+FFN。
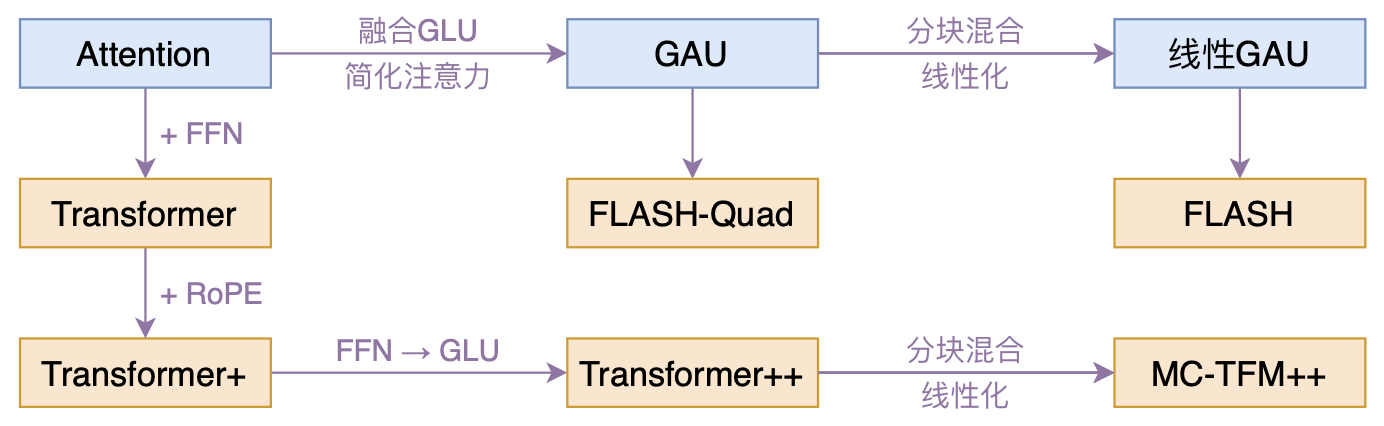
所以,在GAU的实验中,作者都固定$e=2d$,那么“$n$层Attention+$n$层FFN”的标准Transformer模型,对应的就是“$2n$层GAU”的新模型,我们记为FLASH-Quad,其中Quad是“Quadratic”的简写,表明复杂度依然是二次的,至于FLASH的含义,后面再谈。
高效线性 #
其实FLASH-Quad已经是标准Transformer的一个非常优秀的替代品了,但作者们还不满意其二次复杂度,继而提出了具有线性复杂度的FLASH(Fast Linear Attention with a Single Head)。为此,作者提出了一种“分块混合注意力(Mixed Chunk Attention)”的方案,它不单可以用于前述GAU中,也可以用于标准的Attention中,是一种较为通用的线性化技巧。
现有方法 #
主流的高效Transformer工作对Attention的改进思路大体上可以两大类,分别是“稀疏化”和“线性化”。
本文开头提到的《为节约而生:从标准Attention到稀疏Attention》,就是“稀疏化”的工作之一,后面诸如Reformer等也算是此列,还有一些跟Pooling结合的如Linformer也可以理解为广义的“稀疏化”。这类工作的特点是引入一定的归纳先验,强制大部分注意力为0,从而理论上可以少减少计算量。但这种方案的缺点是往往需要专门的编程优化才能实现加速,或者是难以用来做Decoder(Pooling类工作),此外效果好坏比较依赖于其引入的归纳先验,显得不够自然。
至于“线性化”,我们在《线性Attention的探索:Attention必须有个Softmax吗?》有过介绍,研究的人相对多一些,后面的Performer、Nyströmformer以及最近的cosFormer、Flowformer都可以归入此类。简单来看,这类工作是将标准Attention的$\phi(\boldsymbol{Q}\boldsymbol{K}^{\top})\boldsymbol{V}$改为$(\phi_q(\boldsymbol{Q})\phi_k(\boldsymbol{K})^{\top})\boldsymbol{V}=\phi_q(\boldsymbol{Q})(\phi_k(\boldsymbol{K})^{\top}\boldsymbol{V})$从而实现了线性复杂度。这类方法的好处是易于实现,但有两个主要问题,一是低秩性会导致效果明显变差(参考《Transformer升级之路:3、从Performer到线性Attention》);另外是用来做Decoder(Causal)时会牺牲训练并行性,因为它需要转化为RNN来计算,又或者不牺牲并行性,但需要$bhns^2$的空间复杂度,相比于标准Attention的$bhn^2$,起码要$n \gg s^2$才有优势,而哪怕$s=64$,都要$n \gg 4096$了,多数情况下不现实。
分块混合 #
FLASH采取了“局部-全局”分块混合的方式,结合了“稀疏化”和“线性化”的优点。首先,对于长度为$n$的输入序列,我们将它不重叠地划分为$n/c$个长度为$c$的块(不失一般性,假设$c$能被$n$整除,论文取$c=256$),设$\boldsymbol{U}_g,\boldsymbol{V}_g\in\mathbb{R}^{c\times e},\boldsymbol{Z}_g\in\mathbb{R}^{c\times s}$为第$g$块,其中$\boldsymbol{U},\boldsymbol{V},\boldsymbol{Z}$的定义同前。跟式$\eqref{eq:relu-att}$一样,我们将$\boldsymbol{Z}_g$通过4个简单的仿射变换分别得到$\boldsymbol{Q}_g^{\text{quad}},\boldsymbol{K}_g^{\text{quad}},\boldsymbol{Q}_g^{\text{lin}},\boldsymbol{K}_g^{\text{lin}}$。
其中$\boldsymbol{Q}_g^{\text{quad}},\boldsymbol{K}_g^{\text{quad}}$我们用来算块内的自注意力:
\begin{equation}\hat{\boldsymbol{V}}_g^{\text{quad}}=\frac{1}{cs}\text{relu}^2\left(\boldsymbol{Q}_g^{\text{quad}}{\boldsymbol{K}_g^{\text{quad}}}^{\top}\right)\boldsymbol{V}_g\end{equation}
这代表的是每个块的token内部自行交互,本质上也算是“稀疏化”的一种,其复杂度大致是$\mathcal{O}(n/c\times c^2)=\mathcal{O}(nc)$,正比于$n$。实现时相当于头数为$n/c$、序列长度为$c$的多头注意力,可以充分地并行,而如果想要做Decoder,那么mask掉注意力矩阵的上三角部分即可。
剩下的$\boldsymbol{Q}_g^{\text{lin}},\boldsymbol{K}_g^{\text{lin}}$则用来做全局的Attention,我们直接用前述线性Attention的方式来做:
\begin{equation}\hat{\boldsymbol{V}}_g^{\text{lin}}=\frac{1}{n}\boldsymbol{Q}_g^{\text{lin}}\sum_{h=1}^{n/c} {\boldsymbol{K}_h^{\text{lin}}}^{\top}\boldsymbol{V}_h\end{equation}
注意,这个操作跟直接用完整矩阵$\boldsymbol{Q}^{\text{lin}},\boldsymbol{K}^{\text{lin}}\in\mathbb{R}^{n\times s}$与$\boldsymbol{V}$做线性Attention是完全等价的,写成这样只是更好地体现跟分块的联系。如果是做Decoder,那么要防止泄漏未来信息,所以要改为cumsum形式:
\begin{equation}\hat{\boldsymbol{V}}_g^{\text{lin}}=\frac{1}{(g-1)n/c}\boldsymbol{Q}_g^{\text{lin}}\sum_{h=1}^{g-1} {\boldsymbol{K}_h^{\text{lin}}}^{\top}\boldsymbol{V}_h\end{equation}
这种情况下,为了保持并行性,我们只需要$b(n/c)se$的空间复杂度,而如果不分块直接用线性Attention,那么是$bns^2$(要是原始的用法还要加上多头,那就是$bhns^2$),在当前参数设置下有$e/c\ll s$,所以是更省显存了。
最后,将两种Attention结果结合起来,整合到GAU中,得到线性版本的GAU
\begin{equation}\boldsymbol{O}_g=\left[\boldsymbol{U}_g\odot\left(\hat{\boldsymbol{V}}_g^{\text{quad}} + \hat{\boldsymbol{V}}_g^{\text{lin}}\right)\right]\boldsymbol{W}_o\end{equation}
基于线性版本GAU搭建的Transformer模型,便是作者笔下的FLASH模型了。
一些讨论 #
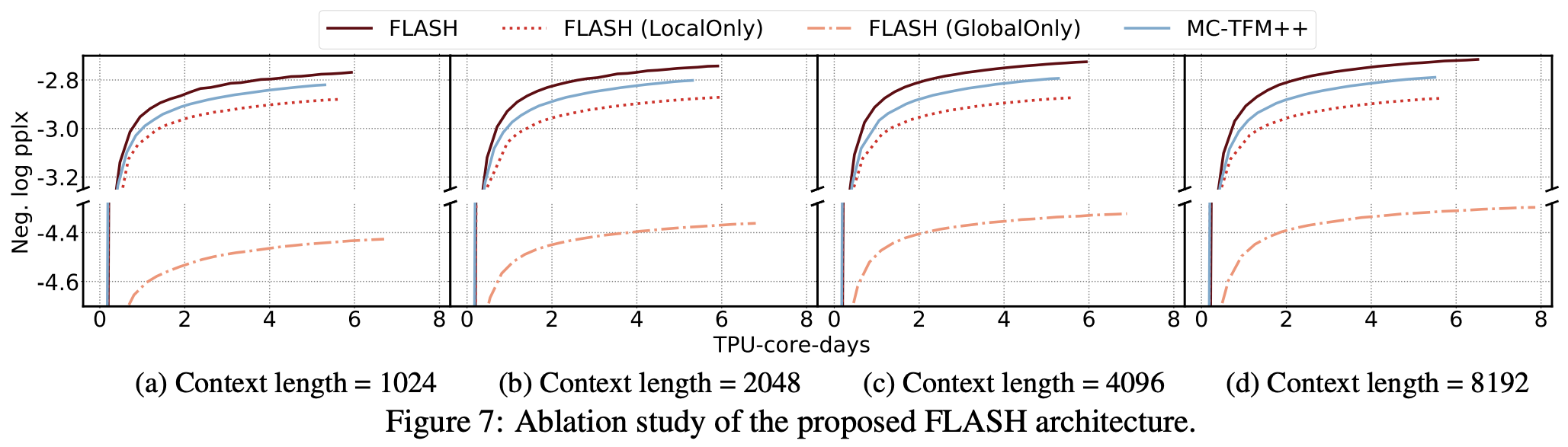
笔者认为,之所以这样分块做“局部-全局”的混合注意力,除了是想降低计算成本外,还因为这样做能得到更贴合实际情况的注意力分布。按照我们对NLP的经验理解,自然语言中的关联主要还是集中在局部的,而全局的、极度长距离的关联虽然存在,但不会是主导地位,所以这种混合式的注意力设计更有利于模型凸出局部关联但不舍弃长程关联。原论文还做了消融实验,显示相对来说局部注意力比全局注意力更重要,而混合式的效果最好。
此外,可能会有些读者担心这种非重叠的分块会不会不利于边界词的预测?原论文提到了这一点,它说引入更复杂的重叠式局部注意力确实有利于提升效果,但也引入了额外的计算成本,在增加同样计算成本的情况下,引入重叠式局部注意力带来的增益还不如直接多加几层目前的非重叠式GAU。所以说,目前的非重叠足够好地平衡了速度和效果。
最后,这种“分块混合”的线性化方案本质上是通用的,它不仅可以用于GAU中,也可以用于标准的Transformer中,即保留标准的Attention+FFN组合,然后Attention用分块混合的方式进行线性化,原论文称之为“MC-TFM”,并也进行了相应的比较,结果显示GAU在线性化方面也显得更有优势。
实验分析 #
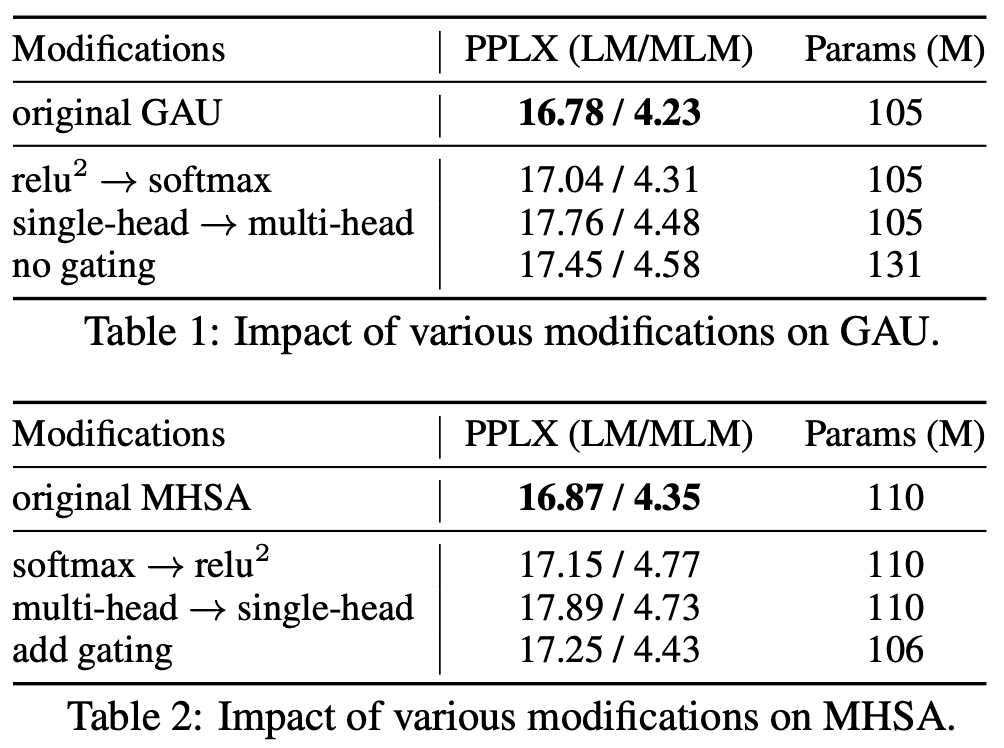
关于GAU和FLASH的实验结果,笔者认为最值得留意的有两个。
第一个是新设计的门控注意力单元GAU与标准的多头注意力之间MHSA的比较,其实也就是FLASH-Quad和标准Transformer的比较了,如下图:
注意横轴是速度,纵轴是效果,这种图越靠近右上角的点意味着越理想(速度和效果都最优),所以上图显示不管哪种规格的模型,GAU都比相应的多头注意力模型更有优势。
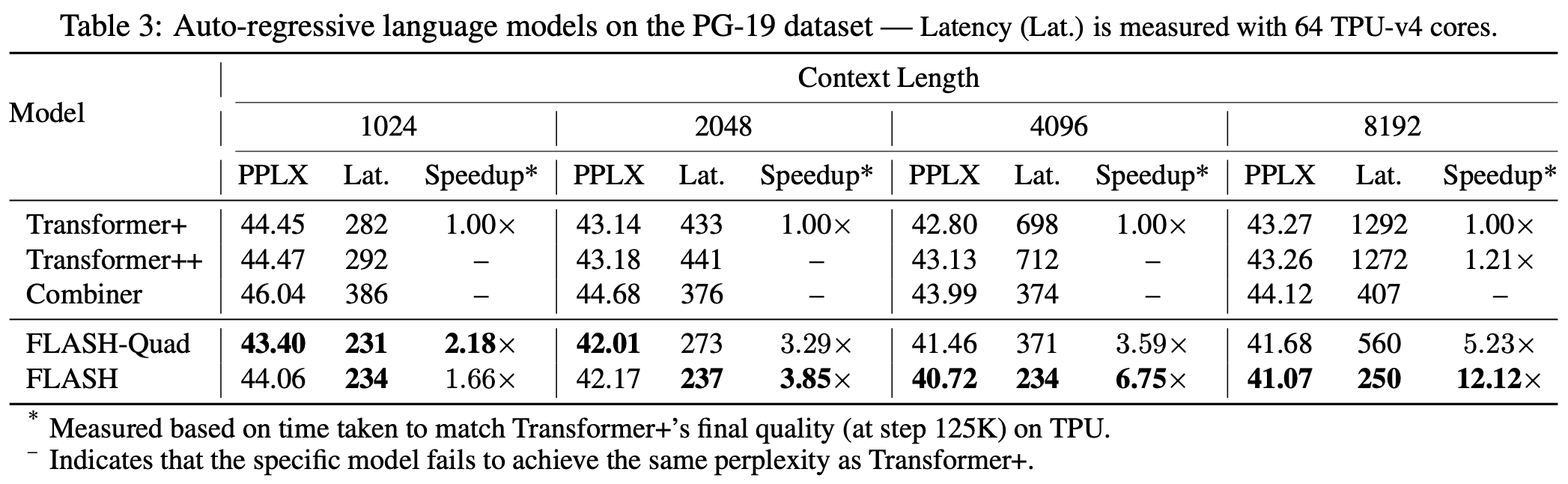
第二个则是FLASH模型的实验表格:
该表格更直接地显示出:
1、尽管FLASH-Quad和Transformer都是二次复杂度,但FLASH-Quad效果更好、速度更快;
2、在序列足较长时,线性复杂度的FLASH比FLASH-Quad更快,并且效果相仿。
说实话,即便是FLASH-Quad这个依然是二次复杂度的模型的速度提升幅度,很多号称是线性复杂度的工作都未必能做到,GAU的强大可见一斑。对了,论文还特别指出笔者之前提的旋转位置编码RoPE能明显提高Transformer和FLASH的效果,所以论文实验的Transformer+、Transformer++、FLASH-Quad和FLASH都是带有RoPE编码的,在此沾沾自喜一下。
另外,上述表格并没有给出显存占用的对比。事实上,笔者测试发现,在base量级和序列长度为1024时,FLASH-Quad可用的最大batch_size将近是Transformer的两倍,这意味着FLASH-Quad明显降低了显存消耗。同时,笔者简单尝试了small版本FLASH-Quad的中文预训练,发现效果甚至比RoFormer(RoPE+Transformer)要好些,所以论文所报告的结果确实不虚。不过最近的卡有限,就没法进行更深入的测试了,以后有新结果再跟大家分享。
延伸思考 #
至此,对GAU、FLASH的介绍也基本结束了。到发博客时,作者还没有在Gihub上开放完整源代码,但是附录已经贴出了几乎可以直接抄来用的关键源码(tensorflow版),所以代码的实现应但是没有困难的,有兴趣有算力的同学,可以自行参考实验。另外论文有什么读不懂的地方,也可以直接参考源代码。
下面进行“挑骨头”环节,说一下我觉得这篇论文还做的不够完美的地方。
首先,笔者认为FLASH-Quad和FLASH解耦得不够好。如本文开头的观点,FLASH-Quad和FLASH都算得上是“重磅”级别的结果,甚至对笔者来说FLASH-Quad更有价值,因为自注意力的二次复杂度本身也带来了足够多的自由度,可以玩很多像UniLM这样的花样,所以FLASH-Quad本身应该是一个很独立、很值得肯定的模型,但在原论文中,它更像是FLASH的一个过渡产品,这我认为是过于“冷落”了FLASH-Quad。幸好,作者单独分离出了GAU的概念,也算是缓解了这个不足。
然后,GAU既可以代替Attention,也可以代替FFN,从设计上来看,它旨在代替的是Self-Attention,作者似乎不关心它对Cross Attention的可代替性,论文也没有相应的实验。那么,GAU是否有可能代替Cross Attention呢?从式$\eqref{eq:mix}$的形式看,理论上是有可能的,但不知道GAU代替Cross Attention时能否依然只保留一个头,因为只需一个头可谓是GAU替代Self Attention的最大亮点了,它是更快更省的关键。此外,论文只做了LM和MLM的语言模型实验,并没有做“预训练+微调”的实验,不确定GAU的迁移性能如何。或许等我有卡了,我也去补充一波实验。
最后,有一个笔者不大理解的地方,就是GAU/FLASH-Quad/FLASH同时用上了加性绝对、加性相对以及RoPE三种位置编码,理论上三者只用其一就行了,笔者自己做的GAU实验也只用RoPE但效果依然挺好,所以这里同时用三种有什么讲究吗?最后,从论文附录所给的源码看,作者并没有仔细处理好padding的问题,以及做Decoder是归一化因子递归也没有写好(前$t$项求和应该除以$t$而不是$n$),这些都是不大不小的可改善的细节。当然,不排除作者的原始代码是正确的,附录只是出于可读性目的做了简化,因为附录里边的代码还是以“伪代码”自称。
本文小结 #
本文介绍了Google新出的一个高效Transformer工作,里边将Attention和FFN融合为一个新的GAU层,从而得到了Transformer变体FLASH-Quad,作者还进一步提出了一种“分块混合”线性化方案,得到了具有线性复杂度的FLASH。目前的实验结果显示,不管FLASH-Quad还是FLASH,跟标准Transformer相比都是更快、更省、更好。也许不久之后,All You Need的就不再是Attention而是GAU了。
转载到请包括本文地址:https://spaces.ac.cn/archives/8934
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Feb. 25, 2022). 《FLASH:可能是近来最有意思的高效Transformer设计 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/8934
@online{kexuefm-8934,
title={FLASH:可能是近来最有意思的高效Transformer设计},
author={苏剑林},
year={2022},
month={Feb},
url={\url{https://spaces.ac.cn/archives/8934}},
}











February 2nd, 2023
苏神请教一下,关于公式6的归一化系数,论文附录伪代码用的块长度,而非序列完整长度,您认为哪种方式更合理一些。
总长度貌似更适合
May 9th, 2023
我想做一个序列的任务,数据集不是很大,然后maxlen大概几十的样子,我想用单个GAU去替换多头注意力,但是我发现dense层参数十几万,测试精度不如多头,是因为太短了吗
太短单头的意义不大,而且不管GAU还是普通的多头注意力机制,都没有明显的inductive bias,在没有预训练的场景下哪个更好,这里边运气成分居多,我倾向于没有标准答案。
May 30th, 2023
[...]FLASH:可能是近来最有意思的高效Transformer设计[...]
July 3rd, 2023
之前Talking Head的特点是多头交互效果很好, 而GAU只要一个头就够了. 如果GAU也做成多头进行Talking head, 不知道效果如何?
多头在长序列时会明显增加显存占用,就是不希望多头。
November 8th, 2023
苏神,请教下您,这种方法可以用在图像上吗
理论上模型不会限制数据类型。但处理图像应该要换为二维的RoPE https://kexue.fm/archives/8397 了。
November 12th, 2023
苏神请教!我目前的任务类似于翻译任务,依然用的是encoder + decoder的seq2seq结构,需要self attention + cross attention
这个gau目前并没有找到cross attention的实现。
那么,如果我想试试这个模型,是不是只能像unilm一样用mask实现seq2seq啊?
谢谢。。。。。
https://github.com/bojone/bert4keras/blob/master/bert4keras/layers.py#L652
我这实现过一个cross attention版本的,供参考。
感谢!
February 7th, 2024
我認為用 $\frac{1}{n^2}$ 是有道理的。原文程式碼這樣寫:
tf.math.square(tf.nn.relu(qk / seq_len + bias))
注意到它是把 qk / seq_len 放在 relu 裡面,然後才平方。表示他們認為 qk 本身就包含句子長度的一次項因子,這應該是合理的。因為 q,k 的維度數量等於序列長度,所以 q*k 加總,它加總的項數就等於序列長度。假設平均每一項的大小差不多,那麼序列越長,加總就跟序列長度的一次成正比。所以他在qk算出來後先除以序列長度,然後才通過relu^2。由於relu(x)在x大於0的時候等於x,所以若 qk 本身已包含序列長度的一次項因子,那麼 relu^2(qk) 結果就會正比於長度的二次項。所以在這裡,先除掉序列長度n 再通過 relu^2,跟先通過relu^2 再除掉n^2 是一樣的。即:
$$
relu^2(\frac{qk}{n}) = \frac{1}{n^2}relu^2(qk)
$$
至於標準注意力所用的softmax,其分子為 $ e^{qk}$,就算 qk 裡面包含了長度因子,也可以視為softmax中的溫度係數T,即:
$$ e^{qk} = e^{\frac{qk}{nT}} = e^{\frac{\frac{qk}{n}}{T}}$$
其中nT=1。
當序列長度越長時,T就越小。所以標準注意力的softmax,可以理解為隨著序列長度變化而自適應調整溫度係數,序列越長,結果就越稀疏。而softmax 分母的作用,在於消除隨序列長度增加的加總項數的影響。
所以,我認為,softmax是很巧妙的把「隨著長度增加自動變稀疏」跟「消除序列長度對加總項數的影響」結合在一起,才這麼有效。
若要設計方法取代softmax,應該要考慮:
1. 如何隨序列長度增加自適應的變稀疏?
2. 最後的weighted sum 需要消除加總項數隨序列長度增加的影響。
從這兩點來看,確實是不需要像 softmax 一樣歸一化的,只要能消除序列長度的因子即可。
在這篇的GAU中,我是沒看到 relu^2 如何能夠達到第一點:隨著長度自適應稀疏。這或許就是你在 https://kexue.fm/archives/9019 這篇中提到的 GAU 長度外推性不好的原因。雖然,若以相同長度的序列來比,relu^2 確實比relu 更稀疏;但是,長度為n跟2n的序列來比,看不出來relu^2 有能夠隨著長度增加變得更稀疏的效果。除非有別的機制,例如在loss中加入隨著長度增加獎勵稀疏,這樣就有可能在序列長度增加的時候,鼓勵他更多輸出0,從而增加稀疏性。
又,從你這篇《如何度量数据的稀疏程度?》 https://kexue.fm/archives/9595 中,有一個稀疏指標的公式:
$$S_{q,p}^*(\boldsymbol{x})=n^{1/p-1/q}\frac{l_q(\boldsymbol{x})}{l_p(\boldsymbol{x})}$$
如果令 $q=1,p \to \infty$ ,則指標變為:
$$S_{1,p}^*(\boldsymbol{x})=n^{-1}\frac{l_1(\boldsymbol{x})}{l_p(\boldsymbol{x})}=\frac{\frac{l_1(\boldsymbol{x})}{n}}{l_p(\boldsymbol{x})}$$
我故意不把分母的 p 改掉,因為實務上我們可能無法計算 $l_\infty$ ,只能用有限的 p 來近似。然而分子這項的n卻是可以準確算出來的。若這裡的 x 是 attention score 中的 qk,那麼把 qk/n 才能消除序列長度的效應。
在attention的例子中,n對應到序列長度。由於序列長度是會變動的,因此必須要把 n 納入稀疏度指標來考慮。但由於padding補0的關係,如果input length來看,都是固定長度,必須要把padding 的0排除。由於$l_0$代表非0的項數,這時可用 $l_0$ 來近似n,得到:
$$S_{1,p}^*(\boldsymbol{x})=\frac{\frac{l_1(\boldsymbol{x})}{l_0(\boldsymbol{x})}}{l_p(\boldsymbol{x})}$$
所以實務上可以這樣操作:
x' = x/l_0(x) ## 除以序列長度因子
x'' = x'*(l_{inf}(x)/l_{inf}(x')) ## 乘以 max(x)/max(x') 值讓 x'' 值的最大值範圍回到原本x 的範圍,避免因序列長度變化使 x'' 值的最大值也跟著被改變。試想,若序列長度從n增加為2n,則 max(x') 會是原本 max(x) 的 1/2。但是以注意力的性質來說,注意力最強的部份,不應該因為序列長度變長就變弱了,應該仍然要維持差不多的強度,這樣不同長度的句子之間的注意力強度才可以比較。
注意到,上面的 $l_0$ 跟 $l_{inf}$ 都可以進行軟化,改用 $l_{0.5}$ 跟 $l_4$ 代替,這樣就可以微分。
再對x計算稀疏指標:
$$S_{1,2}^*(\boldsymbol{x})=\frac{l_1(\boldsymbol{x})}{l_2(\boldsymbol{x})}$$
這時由於前面的階段已經對 x 除以 l_0,因此可以不用把 l_0 放進指標中。這樣所獲得的x,應該對於序列長度變化是較robust的。如此,不同長度序列的attention強度,最大值是可比較的;稀疏性指標的數值在不同長度的序列間也是可比較的。
所以,「除以n」這個操作,不只是直覺的解釋為將序列長度除掉,而是可以從稀疏性指標對序列長度的不變性推導出來。這個長度效應在標準注意力中的softmax被巧妙地吸收了,以至於之前根本就沒注意到。但是,softmax雖然吸收了長度效應,卻無法讓attention weight的最大值在不同長度序列中是可比較的。當序列越長,attention weight的最大值就會被分散掉,因此無法在不同長度的序列中進行有意義的比較。而我的作法可以在消除長度因子後,針對最大值再進行一次縮放,而得到可比較的attention weight,對於可視化來說相當有用。
这里不知道我有没有理解错,你的意思是$x''$的系数程度对长度更robust?但$x''$就是$x$的每个分量都乘以一个相同的倍数得到的吧,这样的操作是不改变原本$x$的系数程度的(哪怕这个倍数跟长度$n$相关)。
@Allen7575|comment-23686
1、qk为什么会“包含了长度因子”,q和k都跟长度无关;
2、softmax也没法随着长度的增加而自适应变得更稀疏,所以才有了 https://kexue.fm/archives/8823 之类的新scale。
March 6th, 2024
你好,对FLASH-QUAD这个稍微有点疑惑,除了在训练阶段能提速之外,在推理阶段两层GAU+softmax要比单层Transformer慢吧(seq < 2048情况下)
我还没有系统比较过推理。不过在短序列情况下,GAU的优势确实是不明显的。
January 8th, 2025
能否请教下,对于(3)式文中说“而如果$A$是全1矩阵,那么它就是普通的注意力机制”。请问这里的普通注意力机制指的是$AV$相当于$(QK^T)V$吗,然后前面的$U$是多出来的门控,$W_o$和Attn中的$W_o$一致,我的理解正确吗?
抱歉,这里应该是$\boldsymbol{U}$,已更正,感谢指出。
January 16th, 2025
能否请教一下,为什么现在的大语言模型不采用GAU呢,这是有什么限制吗?
GAU的Attention是single-head的,这对于大规模并行计算来说反而不是什么好事,同时single-head相比multi-head总让人会担心上下文能力尤其是长文本能力的不足(毕竟少了交互次数)。总的来说,GAU还需要更多scale up的测试和改进。