科学空间|Scientific Spaces

在本系列的前面几篇文章中，我们已经从多个角度来理解了VAE，一般来说，用VAE是为了得到一个生成模型，或者是做更好的编码模型，这都是VAE的常规用途。但除了这些常规应用外，还有一些“小众需求”，比如用来估计$x$的概率密度，这在做压缩的时候通常会用到。

本文就从估计概率密度的角度来了解和推导一下VAE模型。

两个问题

所谓估计概率密度，就是在已知样本$x_1,x_2,\cdots,x_N\sim \tilde{p}(x)$的情况下，用一个待定的概率密度簇$q_{\theta}(x)$去拟合这批样本，拟合的目标一般是最小化负对数似然：
\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log q_{\theta}(x)] = -\frac{1}{N}\sum_{i=1}^N \log q_{\theta}(x_i)\label{eq:mle}\end{equation}

点击阅读全文...

在《训练1000层的Transformer究竟有什么困难？》中我们介绍了微软提出的能训练1000层Transformer的DeepNet技术。而对于DeepNet，读者一般也有两种反应，一是为此感到惊叹而点赞，另一则是觉得新瓶装旧酒没意思。出现后一种反应的读者，往往是因为DeepNet所提出的两个改进点——增大恒等路径权重和降低残差分支初始化——实在过于稀松平常，并且其他工作也出现过类似的结论，因此很难有什么新鲜感。

诚然，单从结论来看，DeepNet实在算不上多有意思，但笔者觉得，DeepNet的过程远比结论更为重要，它有意思的地方在于提供了一个简明有效的梯度量级分析思路，并可以用于分析很多相关问题，比如本文要讨论的“为什么需要残差”，它就可以给出一个比较贴近本质的答案。

增量爆炸

为什么需要残差？答案是有了残差才更好训练深层模型，这里的深层可能是百层、千层甚至万层。那么问题就变成了为什么没有残差就不容易训练深层模型呢？

点击阅读全文...

大概在1年前，我们提出了旋转位置编码（RoPE），并发布了对应的预训练模型RoFormer。随着时间的推移，RoFormer非常幸运地得到了越来越多的关注和认可，比如EleutherAI新发布的60亿和200亿参数的GPT模型中就用上了RoPE位置编码，Google新提出的FLASH模型论文中则明确指出了RoPE对Transformer效果有明显的提升作用。

与此同时，我们也一直在尝试继续加强RoFormer模型，试图让RoFormer的性能“更上一层楼”。经过近半年的努力，我们自认为取得了还不错的成果，因此将其作为“RoFormerV2”正式发布：

Github：https://github.com/ZhuiyiTechnology/roformer-v2

点击阅读全文...

在文章《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》中，我们为生成扩散模型DDPM构建了“拆楼-建楼”的通俗类比，并且借助该类比完整地推导了生成扩散模型DDPM的理论形式。在该文章中，我们还指出DDPM本质上已经不是传统的扩散模型了，它更多的是一个变分自编码器VAE，实际上DDPM的原论文中也是将它按照VAE的思路进行推导的。

所以，本文就从VAE的角度来重新介绍一版DDPM，同时分享一下自己的Keras实现代码和实践经验。

Github地址：https://github.com/bojone/Keras-DDPM

多步突破

在传统的VAE中，编码过程和生成过程都是一步到位的：
\begin{equation}\text{编码:}\,\,x\to z\,,\quad \text{生成:}\,\,z\to x\end{equation}

点击阅读全文...

用理论物理来卷机器学习已经不是什么新鲜事了，比如上个月介绍的《生成扩散模型漫谈（十三）：从万有引力到扩散模型》就是经典一例。最近一篇新出的论文《Self-Supervised Learning based on Heat Equation》，顾名思义，用热传导方程来做（图像领域的）自监督学习，引起了笔者的兴趣。这种物理方程如何在机器学习中发挥作用？同样的思路能否迁移到NLP中？让我们一起来读读论文。

基本方程

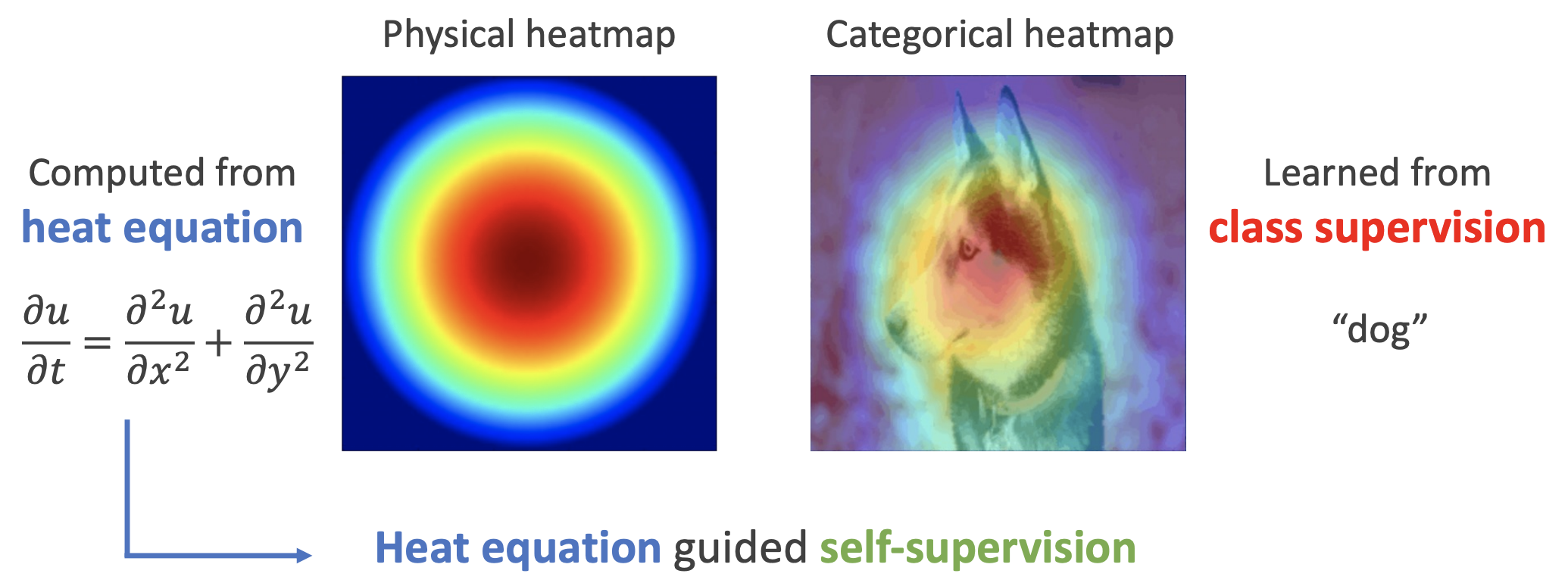
如下图，左边是物理中热传导方程的解，右端则是CAM、积分梯度等显著性方法得到的归因热力图，可以看到两者有一定的相似之处，于是作者认为热传导方程可以作为好的视觉特征的一个重要先验。

热方程的热力图（左）和视觉模型的热力图（右）

点击阅读全文...

众所周知，分类问题的常规评估指标是正确率，而标准的损失函数则是交叉熵，交叉熵有着收敛快的优点，但它并非是正确率的光滑近似，这就带来了训练和预测的不一致性问题。另一方面，当训练样本的预测概率很低时，交叉熵会给出一个非常巨大的损失（趋于$-\log 0^{+}=\infty$），这意味着交叉熵会特别关注预测概率低的样本——哪怕这个样本可能是“脏数据”。所以，交叉熵训练出来的模型往往有过度自信现象，即每个样本都给出较高的预测概率，这会带来两个副作用：一是对脏数据的过度拟合带来的效果下降，二是预测的概率值无法作为不确定性的良好指标。

围绕交叉熵的改进，学术界一直都有持续输出，目前这方面的研究仍处于“八仙过海，各显神通”的状态，没有标准答案。在这篇文章中，我们来学习一下论文《Tailoring Language Generation Models under Total Variation Distance》给出的该问题的又一种简明的候选方案。

点击阅读全文...

前天晚上微信群里有群友提出了一个问题：

对于一个任意整数$N > 100$，求一个近似算法，使得$N=a\times b+c$（其中$a,b,c$都是非负整数），并且令$a+b+c$尽量地小。

初看这道题，笔者第一感觉就是“这还需要算法？”，因为看上去自由度太大了，应该能求出个解析解才对，于是简单分析了一下之后就给出了个“答案”，结果很快就有群友给出了反例。这时，笔者才意识到这题并非那么平凡，随后正式推导了一番，总算得到了一个可行的算法。正当笔者以为这个问题已经结束时，另一个数学群的群友精妙地构造了新的参数化，证明了算法的复杂度还可以进一步下降！

整个过程波澜起伏，让笔者获益匪浅，遂将过程记录在此，与大家分享。

点击阅读全文...

随着MathJax的出现和流行，在网页上显示数学公式便逐渐有了标准答案。然而，MathJax（包括其竞品KaTeX）只是负责将网页LaTeX代码转化为数学公式，对于自适应分辨率方面依然没有太好的办法。像本站一些数学文章，因为是在PC端排版好的，所以在PC端浏览效果尚可，但转到手机上看就可能有点难以入目了。

经过测试，笔者得到了一个方案，让MathJax的数学公式也能像图片一样，随着窗口大小而自适应缩放，从而尽量保证移动端的显示效果，在此跟大家分享一波。

背景思路

这个问题的起源是，即便在PC端进行排版，有时候也会遇到一些单行公式的长度超出了网页宽度，但又不大好换行的情况，这时候一个解决方案是用HTML代码手动调整一下公式的字体大小，比如

<span style="font-size:90%">
    \begin{equation}一个超长的数学公式\end{equation}
</span>

点击阅读全文...