貌离神合的RNN与ODE:花式RNN简介
By 苏剑林 | 2018-06-23 | 100468位读者 | 引用本来笔者已经决心不玩RNN了,但是在上个星期思考时忽然意识到RNN实际上对应了ODE(常微分方程)的数值解法,这为我一直以来想做的事情——用深度学习来解决一些纯数学问题——提供了思路。事实上这是一个颇为有趣和有用的结果,遂介绍一翻。顺便地,本文也涉及到了自己动手编写RNN的内容,所以本文也可以作为编写自定义的RNN层的一个简单教程。
注:本文并非前段时间的热点“神经ODE”的介绍(但有一定的联系)。
RNN基本
什么是RNN?
众所周知,RNN是“循环神经网络(Recurrent Neural Network)”,跟CNN不同,RNN可以说是一类模型的总称,而并非单个模型。简单来讲,只要是输入向量序列$(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_T)$,输出另外一个向量序列$(\boldsymbol{y}_1,\boldsymbol{y}_2,\dots,\boldsymbol{y}_T)$,并且满足如下递归关系
$$\boldsymbol{y}_t=f(\boldsymbol{y}_{t-1}, \boldsymbol{x}_t, t)\tag{1}$$
的模型,都可以称为RNN。也正因为如此,原始的朴素RNN,还有改进的如GRU、LSTM、SRU等模型,我们都称为RNN,因为它们都可以作为上式的一个特例。还有一些看上去与RNN没关的内容,比如前不久介绍的CRF的分母的计算,实际上也是一个简单的RNN。
说白了,RNN其实就是递归计算。
从变分编码、信息瓶颈到正态分布:论遗忘的重要性
By 苏剑林 | 2018-11-27 | 154623位读者 | 引用这是一篇“散文”,我们来谈一下有着千丝万缕联系的三个东西:变分自编码器、信息瓶颈、正态分布。
众所周知,变分自编码器是一个很经典的生成模型,但实际上它有着超越生成模型的含义;而对于信息瓶颈,大家也许相对陌生一些,然而事实上信息瓶颈在去年也热闹了一阵子;至于正态分布,那就不用说了,它几乎跟所有机器学习领域都有或多或少的联系。
那么,当它们三个碰撞在一块时,又有什么样的故事可说呢?它们跟“遗忘”又有什么关系呢?
变分自编码器
在本博客你可以搜索到若干几篇介绍VAE的文章。下面简单回顾一下。
理论形式回顾
简单来说,VAE的优化目标是:
\begin{equation}KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))=\iint \tilde{p}(x)p(z|x)\log \frac{\tilde{p}(x)p(z|x)}{q(x|z)q(z)} dzdx\end{equation}
其中$q(z)$是标准正态分布,$p(z|x),q(x|z)$是条件正态分布,分别对应编码器、解码器。具体细节可以参考《变分自编码器(二):从贝叶斯观点出发》。
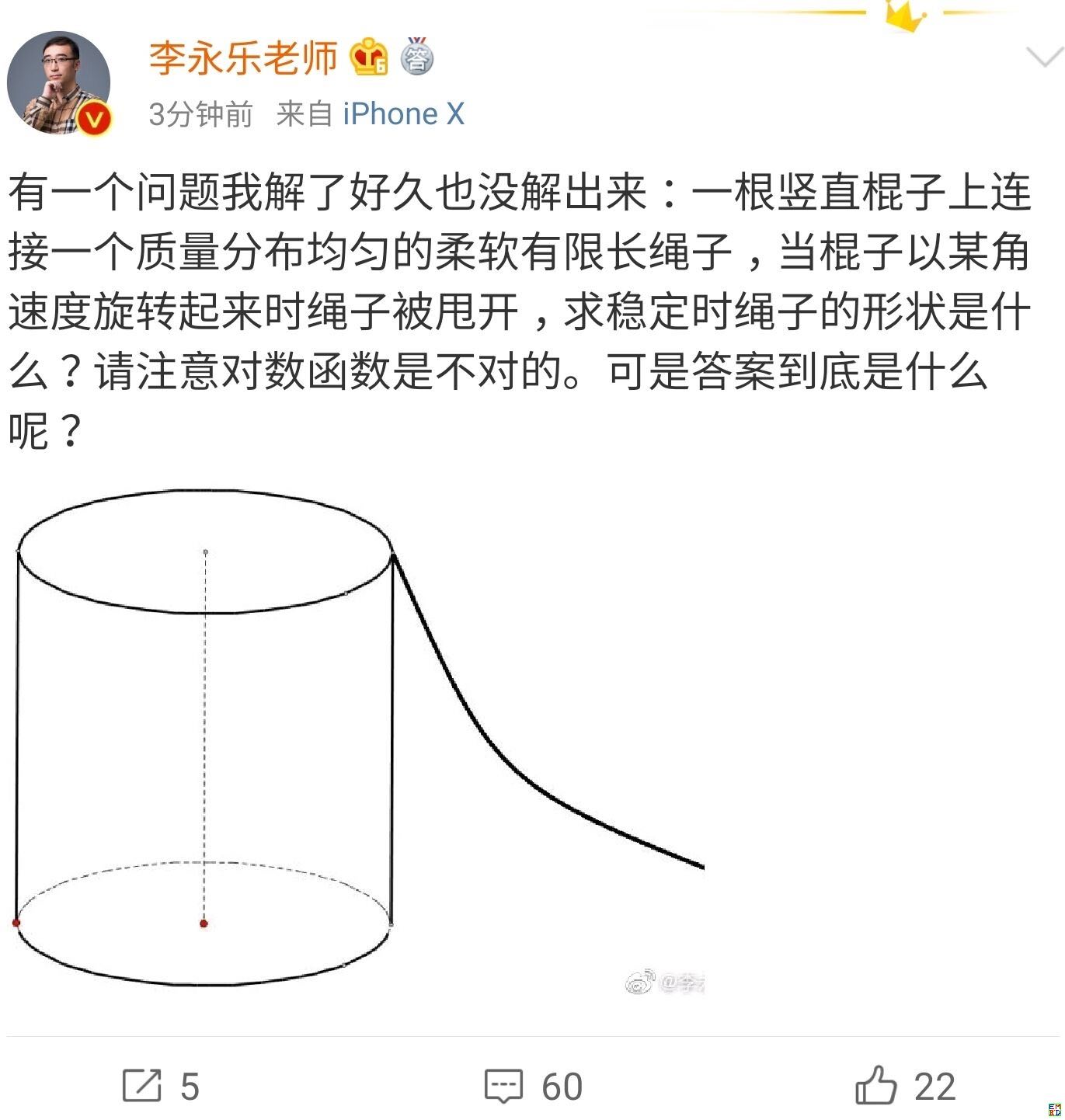
你跳绳的时候,想过绳子的形状曲线是怎样的吗?
By 苏剑林 | 2019-07-06 | 48713位读者 | 引用BN究竟起了什么作用?一个闭门造车的分析
By 苏剑林 | 2019-10-11 | 115204位读者 | 引用BN,也就是Batch Normalization,是当前深度学习模型(尤其是视觉相关模型)的一个相当重要的技巧,它能加速训练,甚至有一定的抗过拟合作用,还允许我们用更大的学习率,总的来说颇多好处(前提是你跑得起较大的batch size)。
那BN究竟是怎么起作用呢?早期的解释主要是基于概率分布的,大概意思是将每一层的输入分布都归一化到$\mathcal{N}(0,1)$上,减少了所谓的Internal Covariate Shift,从而稳定乃至加速了训练。这种解释看上去没什么毛病,但细思之下其实有问题的:不管哪一层的输入都不可能严格满足正态分布,从而单纯地将均值方差标准化无法实现标准分布$\mathcal{N}(0,1)$;其次,就算能做到$\mathcal{N}(0,1)$,这种诠释也无法进一步解释其他归一化手段(如Instance Normalization、Layer Normalization)起作用的原因。
在去年的论文《How Does Batch Normalization Help Optimization?》里边,作者明确地提出了上述质疑,否定了原来的一些观点,并提出了自己关于BN的新理解:他们认为BN主要作用是使得整个损失函数的landscape更为平滑,从而使得我们可以更平稳地进行训练。
本博文主要也是分享这篇论文的结论,但论述方法是笔者“闭门造车”地构思的。窃认为原论文的论述过于晦涩了,尤其是数学部分太不好理解,所以本文试图尽可能直观地表达同样观点。
(注:阅读本文之前,请确保你已经清楚知道BN是什么,本文不再重复介绍BN的概念和流程。)
L2正则没有想象那么好?可能是“权重尺度偏移”惹的祸
By 苏剑林 | 2020-08-14 | 35185位读者 | 引用L2正则是机器学习常用的一种防止过拟合的方法(应该也是一道经常遇到的面试题)。简单来说,它就是希望权重的模长尽可能小一点,从而能抵御的扰动多一点,最终提高模型的泛化性能。但是读者可能也会发现,L2正则的表现通常没有理论上说的那么好,很多时候加了可能还有负作用。最近的一篇文章《Improve Generalization and Robustness of Neural Networks via Weight Scale Shifting Invariant Regularizations》从“权重尺度偏移”这个角度分析了L2正则的弊端,并提出了新的WEISSI正则项。整个分析过程颇有意思,在这里与大家分享一下。
相关内容
这一节中我们先简单回顾一下L2正则,然后介绍它与权重衰减的联系以及与之相关的AdamW优化器。
L2正则的理解
为什么要添加L2正则?这个问题可能有多个答案。有从Ridge回归角度回答的,有从贝叶斯推断角度回答的,这里给出从扰动敏感性的角度的理解。
殊途同归的策略梯度与零阶优化
By 苏剑林 | 2020-09-15 | 54851位读者 | 引用深度学习如此成功的一个巨大原因就是基于梯度的优化算法(SGD、Adam等)能有效地求解大多数神经网络模型。然而,既然是基于梯度,那么就要求模型是可导的,但随着研究的深入,我们时常会有求解不可导模型的需求,典型的例子就是直接优化准确率、F1、BLEU等评测指标,或者在神经网络里边加入了不可导模块(比如“跳读”操作)。
本文将简单介绍两种求解不可导的模型的有效方法:强化学习的重要方法之一策略梯度(Policy Gradient),以及干脆不需要梯度的零阶优化(Zeroth Order Optimization)。表面上来看,这是两种思路完全不一样的优化方法,但本文将进一步证明,在一大类优化问题中,其实两者基本上是等价的。
后台提示,本文是科学空间的第1000篇文章。
本想写下一篇文章的,但是看到这个提示,就先瞎写个水文纪念一下。都说人老了就喜欢各种感叹,这话还真不假。看到别人高考来个感想,博客十周年了来个感想,现在第1000篇文章了也来个感想,似乎总想找点理由感叹一下一样。那今天又能扯些啥犊子呢?
首先,自恋一下。1000篇文章,如果要印刷下来,就算每篇文章印一页,那也能印个1000页了,相信不少人都没捧起过1000页的书吧(我还真读过,有文章为证:《哈哈,我的“〈圣经〉”到了》),我居然能写个1000篇,也是挺佩服自己的。当然,早期的文章有部分是转载的,不是全部都自己写的,不过还是坚持了不少原创内容,而且就算是转载的也是经过自己编辑整理的,不算纯Copy,所以也勉强能说的过去吧。
然后,庆幸一下。博客开始的主题是天文和科普,后来慢慢偏向了理论物理和数学,现在则偏向了机器学习,但不管怎样,总算很庆幸地在科学这条路坚持了下来。虽然没有像幼时设想的那样成为一名真正的自然科学家/数学家,但终究有点相关,闲时依然可以做做科学计算,勉强也对得起当初的梦想。
多任务学习漫谈(一):以损失之名
By 苏剑林 | 2022-01-18 | 147059位读者 | 引用能提升模型性能的方法有很多,多任务学习(Multi-Task Learning)也是其中一种。简单来说,多任务学习是希望将多个相关的任务共同训练,希望不同任务之间能够相互补充和促进,从而获得单任务上更好的效果(准确率、鲁棒性等)。然而,多任务学习并不是所有任务堆起来就能生效那么简单,如何平衡每个任务的训练,使得各个任务都尽量获得有益的提升,依然是值得研究的课题。
最近,笔者机缘巧合之下,也进行了一些多任务学习的尝试,借机也学习了相关内容,在此挑部分结果与大家交流和讨论。
加权求和
从损失函数的层面看,多任务学习就是有多个损失函数$\mathcal{L}_1,\mathcal{L}_2,\cdots,\mathcal{L}_n$,一般情况下它们有大量的共享参数、少量的独立参数,而我们的目标是让每个损失函数都尽可能地小。为此,我们引入权重$\alpha_1,\alpha_2,\cdots,\alpha_n\geq 0$,通过加权求和的方式将它转化为如下损失函数的单任务学习
\begin{equation}\mathcal{L} = \sum_{i=1}^n \alpha_i \mathcal{L}_i\label{eq:w-loss}\end{equation}
在这个视角下,多任务学习的主要难点就是如何确定各个$\alpha_i$了。










最近评论