[SETI-50周年]茫茫宇宙觅知音
By 苏剑林 | 2011-02-03 | 20261位读者 | 引用转载自2011年1月的《天文爱好者》 作者:薛国轩
“多萝西计划”再探地外文明
据美国空间网站2010年11月13日报道,在人类“探索地外文明”(英文缩写为SETI)50周年纪念之际,世界多个国家的天文学家从本月起再度展开“且听外星人”的联合行动,以延续开始于1960年的“奥兹玛计划”。新的探索活动被命名为“多萝西计划”(Project Dorothy),已于11月5日正式启动,将持续整整一个月时间,来自澳大利亚、日本、韩国、意大利、荷兰、法国、阿根廷和美国的天文学家参与其中。他们将把大大小小的望远镜指向地球周围的一些星球,以期收听到外星人的“天外来音”。
科学空间:2011年4月重要天象
By 苏剑林 | 2011-04-04 | 27227位读者 | 引用新科学家:割裂时间空间,统一相对论量子论
By 苏剑林 | 2013-01-16 | 28084位读者 | 引用这篇文章源于《新科学家》2010年8月7日刊,它介绍了物理学家Horava为了统一相对论和量子力学,把广义相对论的时空联系割裂的尝试。在相对论中,时间和空间结合成了不可分割的整体。而现在,有物理学家却要把时间与空间分开,来建立让广义相对论和量子力学相调和的统一理论。我对这个理论挺感兴趣的,当然,我还没有能力弄懂它。只是它符合了我们大多数人的一个直觉,就是时间总有跟空间不同的地方,它们之间不应该完全等同起来。不过,事实如何,只有未来的实验能够严重了。
本文并没有官方的中文译文,现载的译文来自“译言网”。译文有一些翻译不大正当的地方,由于时间限制,无法一一修正,但是我觉得对于理解本文内容已经足够了。如果有疑问,不妨参考后边的英文原文,并在此提出与大家讨论。
对爱因斯坦的反思:空间-时间耦合的物理数学的终结
纠结于融合引力和量子力学的物理学家们正向着一个受到铅笔芯启发的理论欢呼雀跃,这个理论可以很简单地让他们取得成功。
它曾是一个改变了我们思考空间和时间的方式的报告。那一年是1908年,德国数学家赫尔曼-闵可夫斯基正尝试着理解爱因斯坦火热的新思想——即我们现在所熟知的狭义相对论,它描述当物质运动很快时它们是如何收缩以及时间是如何扭曲的。“从此独立的空间和时间将注定淡出到纯粹的虚幻中,”闵可夫斯基说道:“而只有两者的统一才能保证一个独立的现实世界。”
【理解黎曼几何】5. 黎曼曲率
By 苏剑林 | 2016-10-18 | 56296位读者 | 引用现在我们来关注黎曼曲率。总的来说,黎曼曲率提供了一种方案,让身处空间内部的人也能计算自身所处空间的弯曲程度。俗话说,“不识庐山真面目,只缘身在此山中”,还有“当局者迷,旁观者清”,等等,因此,能够身处空间之中而发现空间中的弯曲与否,是一件很了不起的事情,就好像我们已经超越了我们现有的空间,到了更高维的空间去“居高临下”那样。真可谓“心有多远,路就有多远,世界就有多远”。
如果站在更高维空间的角度看,就容易发现空间的弯曲。比如弯曲空间中有一条测地线,从更高维的空间看,它就是一条曲线,可以计算曲率等,但是在原来的空间看,它就是直的,测地线就是直线概念的一般化,因此不可能通过这种途径发现空间的弯曲性,必须有一些迂回的途径。可能一下子不容易想到,但是各种途径都殊途同归后,就感觉它是显然的了。
怎么更好地导出黎曼曲率来,使得它能够明显地反映出弯曲空间跟平直空间的本质区别呢?为此笔者思考了很长时间,看了不少参考书(《引力与时空》、《场论》、《引力论》等),比较了几种导出黎曼曲率的方式,简要叙述如下。
玩转Keras之seq2seq自动生成标题
By 苏剑林 | 2018-09-01 | 367649位读者 | 引用话说自称搞了这么久的NLP,我都还没有真正跑过NLP与深度学习结合的经典之作——seq2seq。这两天兴致来了,决定学习并实践一番seq2seq,当然最后少不了Keras实现了。
seq2seq可以做的事情非常多,我这挑选的是比较简单的根据文章内容生成标题(中文),也可以理解为自动摘要的一种。选择这个任务主要是因为“文章-标题”这样的语料对比较好找,能快速实验一下。
seq2seq简介
所谓seq2seq,就是指一般的序列到序列的转换任务,比如机器翻译、自动文摘等等,这种任务的特点是输入序列和输出序列是不对齐的,如果对齐的话,那么我们称之为序列标注,这就比seq2seq简单很多了。所以尽管序列标注任务也可以理解为序列到序列的转换,但我们在谈到seq2seq时,一般不包含序列标注。
要自己实现seq2seq,关键是搞懂seq2seq的原理和架构,一旦弄清楚了,其实不管哪个框架实现起来都不复杂。早期有一个第三方实现的Keras的seq2seq库,现在作者也已经放弃更新了,也许就是觉得这么简单的事情没必要再建一个库了吧。可以参考的资料还有去年Keras官方博客中写的《A ten-minute introduction to sequence-to-sequence learning in Keras》。
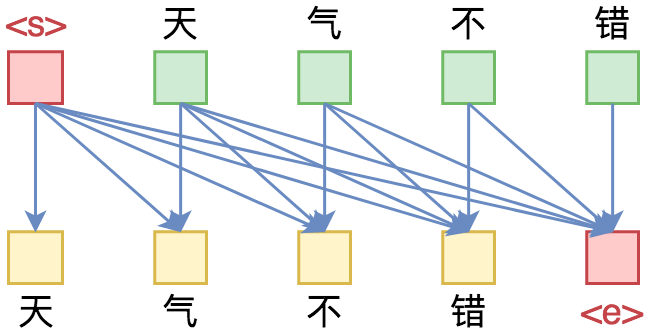
从语言模型到Seq2Seq:Transformer如戏,全靠Mask
By 苏剑林 | 2019-09-18 | 331791位读者 | 引用相信近一年来(尤其是近半年来),大家都能很频繁地看到各种Transformer相关工作(比如Bert、GPT、XLNet等等)的报导,连同各种基础评测任务的评测指标不断被刷新。同时,也有很多相关的博客、专栏等对这些模型做科普和解读。
俗话说,“外行看热闹,内行看门道”,我们不仅要在“是什么”这个层面去理解这些工作,我们还需要思考“为什么”。这个“为什么”不仅仅是“为什么要这样做”,还包括“为什么可以这样做”。比如,在谈到XLNet的乱序语言模型时,我们或许已经从诸多介绍中明白了乱序语言模型的好处,那不妨更进一步思考一下:
为什么Transformer可以实现乱序语言模型?是怎么实现的?RNN可以实现吗?
本文从对Attention矩阵进行Mask的角度,来分析为什么众多Transformer模型可以玩得如此“出彩”的基本原因,正如标题所述“Transformer如戏,全靠Mask”,这是各种花式Transformer模型的重要“门道”之一。
读完本文,你或许可以了解到:
1、Attention矩阵的Mask方式与各种预训练方案的关系;
2、直接利用预训练的Bert模型来做Seq2Seq任务。
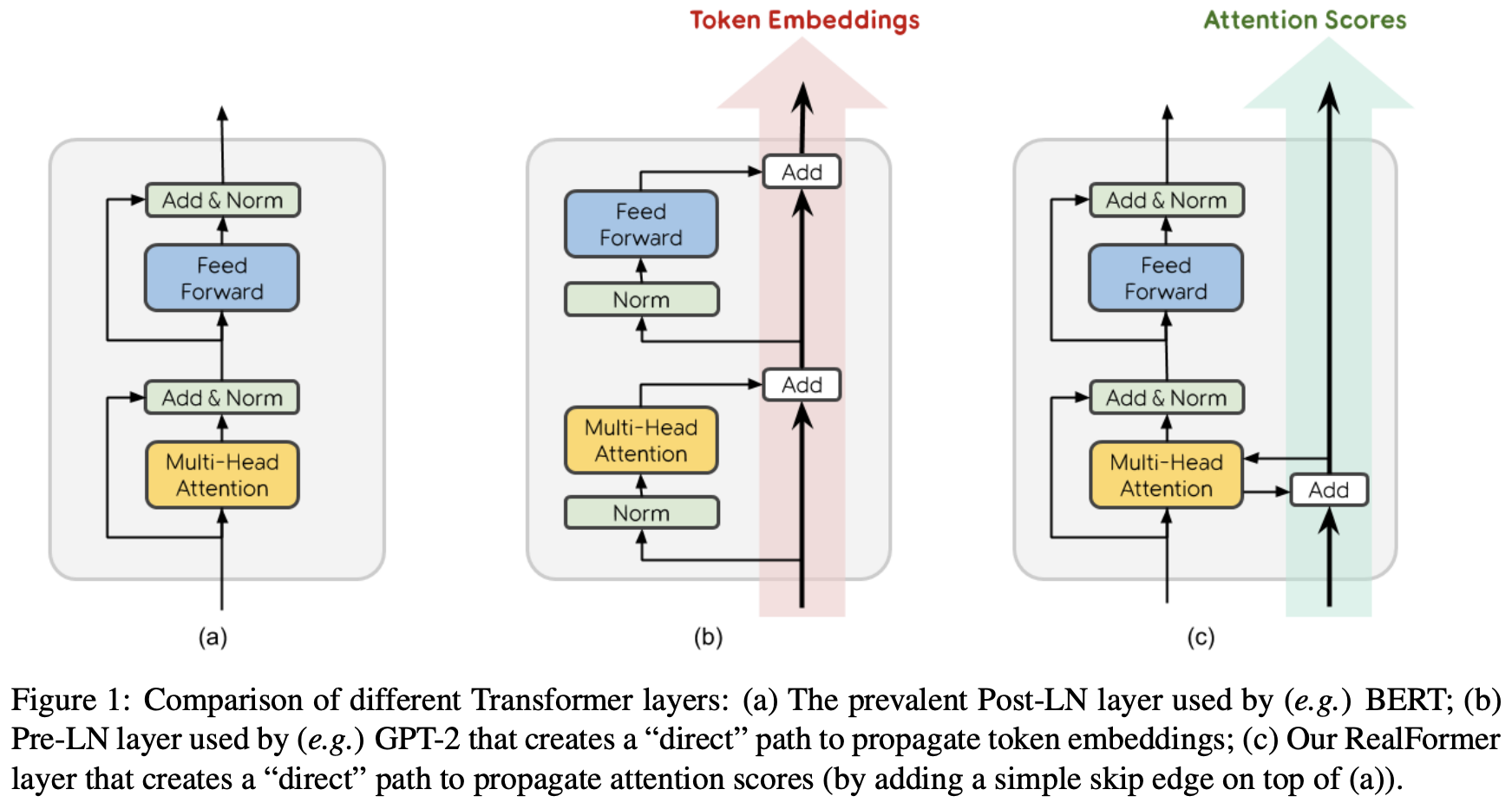
RealFormer:把残差转移到Attention矩阵上面去
By 苏剑林 | 2020-12-24 | 96280位读者 | 引用大家知道Layer Normalization是Transformer模型的重要组成之一,它的用法有PostLN和PreLN两种,论文《On Layer Normalization in the Transformer Architecture》中有对两者比较详细的分析。简单来说,就是PreLN对梯度下降更加友好,收敛更快,对训练时的超参数如学习率等更加鲁棒等,反正一切都好但就有一点硬伤:PreLN的性能似乎总略差于PostLN。最近Google的一篇论文《RealFormer: Transformer Likes Residual Attention》提出了RealFormer设计,成功地弥补了这个Gap,使得模型拥有PreLN一样的优化友好性,并且效果比PostLN还好,可谓“鱼与熊掌兼得”了。
对比学习可以使用梯度累积吗?
By 苏剑林 | 2021-06-17 | 61320位读者 | 引用在之前的文章《用时间换取效果:Keras梯度累积优化器》中,我们介绍过“梯度累积”,它是在有限显存下实现大batch_size效果的一种技巧。一般来说,梯度累积适用的是loss是独立同分布的场景,换言之每个样本单独计算loss,然后总loss是所有单个loss的平均或求和。然而,并不是所有任务都满足这个条件的,比如最近比较热门的对比学习,每个样本的loss还跟其他样本有关。
那么,在对比学习场景,我们还可以使用梯度累积来达到大batch_size的效果吗?本文就来分析这个问题。
简介
一般情况下,对比学习的loss可以写为
\begin{equation}\mathcal{L}=-\sum_{i,j=1}^b t_{i,j}\log p_{i,j} = -\sum_{i,j=1}^b t_{i,j}\log \frac{e^{s_{i,j}}}{\sum\limits_j e^{s_{i,j}}}=-\sum_{i,j=1}^b t_{i,j}s_{i,j} + \sum_{i=1}^b \log\sum_{j=1}^b e^{s_{i,j}}\label{eq:loss}\end{equation}
这里的$b$是batch_size;$t_{i,j}$是事先给定的标签,满足$t_{i,j}=t_{j,i}$,它是一个one hot矩阵,每一列只有一个1,其余都为0;而$s_{i,j}$是样本$i$和样本$j$的相似度,满足$s_{i,j}=s_{j,i}$,一般情况下还有个温度参数,这里假设温度参数已经整合到$s_{i,j}$中,从而简化记号。模型参数存在于$s_{i,j}$中,假设为$\theta$。









最近评论