The Astroncial Events Of 2010
1月1日月偏食,2:51初亏,3:23食甚,3:54复圆。食分0.082。
1月3日 火星合月
1月4日 象限仪流星雨极大
1月5日 水星下合日
1月6日 16时土星合月
1月12日 金星上合日
1月15日 日环食,我国各地从15时-15时30分初亏,云南,四川,重庆,湖北,河南,山东的部分地区可见环食。1时土星留,变为逆行。
1月16日 水星留,变为顺行。金星合月。
1月25日 19时月掩昴星团
1月27日 水星西大距
1月29日 19时42分火星冲日。-1.32等
1月30日 9时火星合月
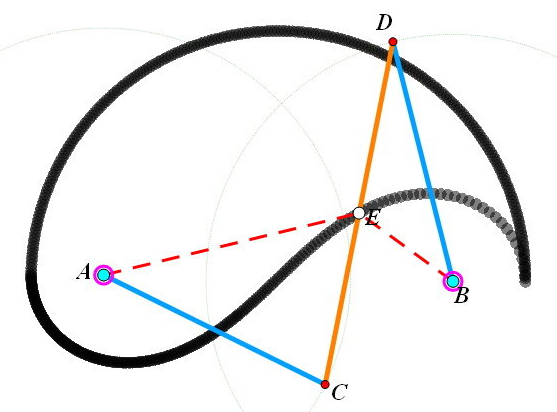
唠叨下,关于三体问题周期轨道
By 苏剑林 | 2011-01-26 | 33366位读者 | 引用[更新]将向量乘法“退化”到复数
By 苏剑林 | 2011-02-04 | 58634位读者 | 引用向量有两个乘法:点乘和叉乘,其结果又分别叫做数量积和向量积。在很多情况下,用这两个定义的乘法运算都能够给我们带来很大的方便(其实它就是在实际问题中抽象出来的)。不过,也有相当一部分的二维问题用复数来描述更为简洁。于是,为了整合两者的巧妙之处,有必要把向量的两个乘法运算“退化”到复数中去(为什么用“退化”?因为向量是多维的,可以是3维、4维等,而复数运算只是二维的,很明显这是一种“退化”而不是“拓展”^_^)
运算法则:
点乘:
总法则:$Z_1 \cdot Z_2=|Z_1||Z_2|\cos(arg\frac{Z_2}{Z_1})$
$$\begin{aligned}1\cdot i=0 \\ i\cdot i=1 \\ \exp(i\theta)\cdot \exp(i\varphi)=\cos(\varphi -\theta) \\ iexp(i\theta)\cdot \exp(i\varphi)=-\sin(\theta-\varphi ) \\ Z_1 \cdot Z_2=Z_1 \bar{Z}_2+Z_2 \bar{Z}_1\end{aligned}$$
新春快乐!2011年2月重要天象
By 苏剑林 | 2011-02-01 | 30773位读者 | 引用相对于其他月份,2月的天空总显得有些寂寞。不过,这并不影响我们开心的情绪。因为通常中国最重要的节日——春节都发生在二月,今年也不例外。春节是农历年的开始,对中国人来说,它才是真正的2011的第一天!新年伊始,科学空间大家天天快乐,心想事成,愿BoJone的人生之旅上能够一直与各位科学爱好者相伴。
天象大观:
01日 金星距太阳: 45.4° W
05日 00:49 火星合日
08日 半人马α流星雨极大
12日 05:32 月合昴宿星团: 1.5° N
17日 17:15 海王星合日
22日 09:02 月合角宿一: 2.8° N
25日 13:26 月合心宿二: 2.9° S
25日 16:27 水星上合日.
[春礼]《方程与宇宙》:圆形限制性三体问题(七)
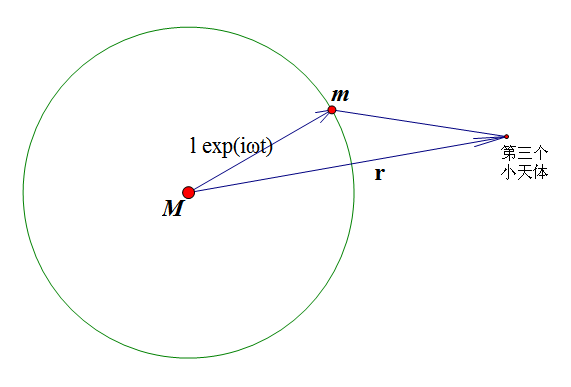
By 苏剑林 | 2011-02-04 | 24322位读者 | 引用平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正!!
寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破,于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”,遗憾的是,“有心栽花花不开”,到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”,也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”,经过一番思考,利用这些天的思考方法重新推导出了其运动方程和能量积分,也算是“意外收获”在此作为春节礼物与大家分享。
所谓“圆形限制性三体问题”,就是指两个大质量天体(质点)在它们相互引力作用下做圆周运动,假设第三天体(质量趋于0)只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分,而这个“限制性模型”能够把问题化简不少(不过还是不能积分出来的),因此也得到了一定应用。它的应用条件是:第三体质量小(如当前航天器与地球、太阳)、短程。注意短程也是相当重要的条件之一,注意短程也是相当重要的条件之一,质量越小应用范围越大。要是质量大的话,就不能计算太长的路程。








最近评论