26
Jan
唠叨下，关于三体问题周期轨道
By 苏剑林 | 2011-01-26 | 33360位读者 | 引用
23
Apr
看完了刘亦菲版《倩女幽魂》
By 苏剑林 | 2011-04-23 | 32249位读者 | 引用自《仙剑奇侠传1》开始，BoJone一直都有追看刘亦菲和胡歌的影视作品，尤其是古装片。胡歌版的《神雕英雄传》、《仙剑奇侠传3》连续剧分别只花了4天时间就把它们看完了（有点狂...），还有他的《神话》等。至于刘亦菲，在我的印象里她这两年没有拍过古装片了，上一部好像就是《功夫之王》了，不过这部电影我不大喜欢（有点看不懂...）。不过刘亦菲的几部古装连续剧，如《神雕侠侣》、《天龙八部》还有《仙剑奇侠传1》中的“神仙姐姐”形象颇让人深刻，也许这正是她的清纯气质吧。
倩女幽魂
我记得去年就在广州日报上看到新版《倩女幽魂》的拍摄消息了，一直都有关注其拍摄进度。好像是在本月初就定下4月22日公映了，但事实上提前公映了。据说影迷本对这部影片不抱太大希望，但是上映后人们大都改观了，好评很多，票房也一路飙升。
其实BoJone是不懂得去欣赏一部电影的。只要影片中的情节不是特别地烂，我都觉得影片不错。看了这句话，一些资深影迷基本可以忽略我了，因为本文几乎没有什么可参考的价值。^_^
15
May
地球引力场的悬链线方程
By 苏剑林 | 2011-05-15 | 62767位读者 | 引用之前曾在《自然极值》系列文章中提到过均匀重力场下的悬链线形状问题，并且在那文章中向读者提出：在一个质点（地球）引力场中的悬链线形状会是怎么样的。说实话，提出这个问题的时候，我还不懂怎么解答这个问题，不过现在会了，回头一看，已经几个月了，时间过得真快...
与之前的思路一样，我们依旧采用的是“平衡态公理”，即总势能最小。从天体力学中我们知道，任意两个质点间的势能为$-\frac{Gm_1 m_2}{r}$。对于本题的悬链线问题，我们可以把地球放到坐标原点位置，而悬链的两个固定点分别为$(x_1,y_1)$和$(x_2,y_2)$，链的总长度为l。即
$$\int_{x_1}^{x_2} \sqrt{dx^2+dy^2}=l$$
28
May
遐思1：n次代数方程的解可以这样表示吗？
By 苏剑林 | 2011-05-28 | 29757位读者 | 引用打从科学空间建立起，就已经设立了“问题百科”这一个分类，但内容一直都很少，主要是平时太懒去总结一些问题。现在得要养成善于思考、总结的习惯了。
前几天到网上印刷了《天遇》和《无法解出的方程》来阅读，两者都是我很感兴趣的书。想当初在初中阶段阅读《数学史选讲》时，我最感兴趣的就是解方程方面的内容（根式解），通过研究理解了1到4次方程的求根公式，并通过阅读知道了4次以上的代数方程没有一般的根式可解。这在当时是多么值得高兴的一件事情！！
现在，稍稍阅读了《无法解出的方程》后，结合我之前在代数方程方面的一些总结，提出一个问题：
若任意的一元n次方程$\sum_{i=0}^{n} a_i x^i=0$的根记为$x_i=R_{n,i}(a_0,a_1,...,a_n)$
那么，是否存在大于3的n，使得任意的一元(n+1)次方程的根能够用加、减、乘、除、幂、开方以及$R_{j,i}$（j可以是1到n的任意整数）通过有限步骤运算出来？
这个问题可以换一个近似但不等价的说法：
若一元1次、2次、...、n次均可以根式解答，那么一元(n+1)次方程能否有根式解？
也就是说，(n+1)次方程的根能够表示成 1到n次方程的根与加、减、乘、除、幂、开方的有限次运算？
（不考虑前提的正确与否，显然n=4已经不成立了，当时n=5,6,7,8,...等有没有可能呢？）
期待有人能够解决^_^
6
Jun
只要我们曾经拥有过——《萍聚》
By 苏剑林 | 2011-06-06 | 22316位读者 | 引用这首歌是凤儿介绍的，去年我们学校高一夏令营的“主题歌曲”。她说歌词写得很好，我感觉也挺不错的^_^
萍，指的是漂浮在水面上的一种藻类，风吹过来，它们就会在风的作用力下聚在一起。人好象是浮在水面上的荷叶，聚散不过都是风吹动所致，到处飘散而已。因此便有了“萍水相逢”这一成语，指的是无心的邂逅或偶然的相遇。“萍聚”亦然。
曾有宋词写道“风中柳絮水中萍,聚散两无情”，这便让我们倍感人生悲欢离合的无奈。在这个充斥着高考的离别的六月里，离愁味道更浓了。可是，不论如何，明天的事情与我们无关，我们要珍惜今天事，珍惜今天人，尽我所能把握好我所拥有的。正如——
Cherish someone special for you and let them know you cherish them.
这样，当我们真的面临无可奈何的离别时，也能够含泪而微笑地挥手，唱着“只要我们曾经拥有过...”。这就是《萍聚》的声音！
6
Jul
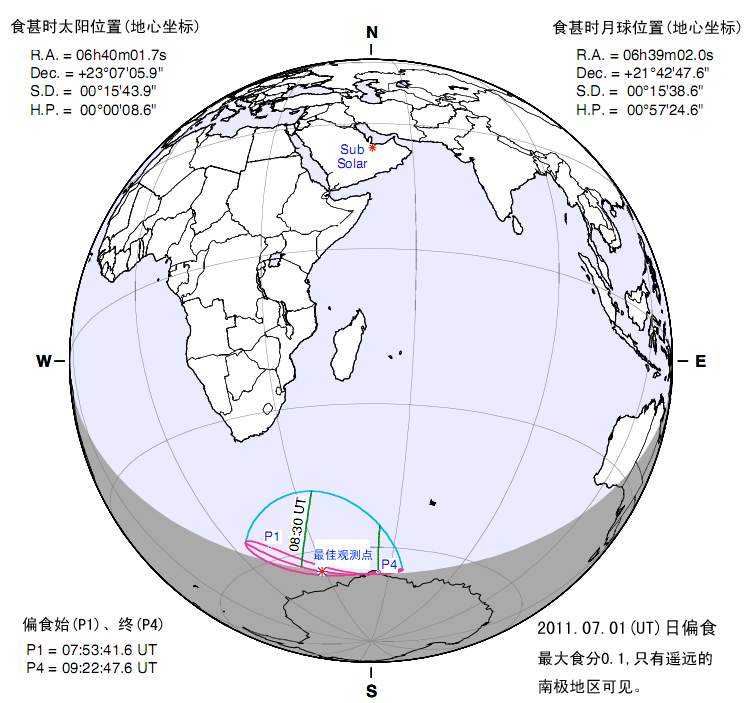
科学空间：2011年7月重要天象
By 苏剑林 | 2011-07-06 | 23302位读者 | 引用
30
Jul
IMO42-1，我也会做几何题
By 苏剑林 | 2011-07-30 | 29048位读者 | 引用七月再次“农忙”，农村里要插秧了，播下种苗，等待再次收获的季节^_^
我一直觉得我的数学能力偏向于分析计算而不擅长于几何，纵使遇到几何问题，也是满脑子的解析几何做法，没有纯几何的美。而这几天为了加强数学竞赛题目的能力，我一直在看IMO的题目，并且企图独立做出一些题目，但都无果。我比较感兴趣的是不等式，我感觉一道简单的式子，不用太多的文字就可以讲清楚的题目非不等式莫属，但是IMO的不等式题实在高深，我还没有能够独立做出一道来（参考答案可以看懂，只是想不到思路），或许是我在努力追求统一的方法而不肯研究那些特定的技巧的原因吧。不料今天看了一下2001年IMO的几何题目，发现我可能将它做出来，于是研究了一会，最终很幸运地做了出来。虽然不是最简单的方法，但也与大家分享一下。
IMO-42-1
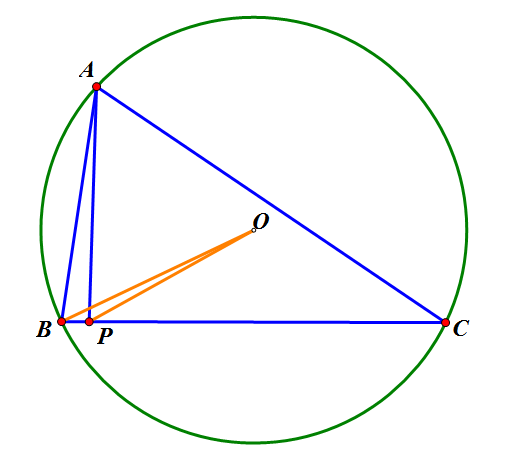
如图，O是锐角三角形ABC的外心，AP是三角形的垂线段，∠B-∠C不小于30°。证明∠BAC+∠BOP < 90°
最近评论