科学空间|Scientific Spaces

这篇文章分享一下笔者关于多模态模型架构的一些闭门造车的想法，或者说一些猜测。

最近Google的Gemini 1.5和OpenAI的Sora再次点燃了不少人对多模态的热情，只言片语的技术报告也引起了大家对其背后模型架构的热烈猜测。不过，本文并非是为了凑这个热闹才发出来的，事实上其中的一些思考由来已久，最近才勉强捋顺了一下，遂想写出来跟大家交流一波，刚好碰上了两者的发布。

事先声明，“闭门造车”一词并非自谦，笔者的大模型实践本就“乏善可陈”，而多模态实践更是几乎“一片空白”，本文确实只是根据以往文本生成和图像生成的一些经验所做的“主观臆测”。

问题背景

首先简化一下问题，本文所讨论的多模态，主要指图文混合的双模态，即输入和输出都可以是图文。可能有不少读者的第一感觉是：多模态模型难道不也是烧钱堆显卡，Transformer“一把梭”，最终“大力出奇迹”吗？

点击阅读全文...

时至目前为止，理论物理上最深奥的问题之一，就是调和广义相对论与量子力学，而一个令物理学家们无比兴奋的，同时也争论不休的量子引力新模型，是否能重新书写物理学理论？针对不久前诞生于美国劳伦斯伯克利实验室的“霍扎瓦模型”，美国得克萨斯A&M大学科学家对其进一步研究后得出中肯的结论，并将结果与值得商榷的内容发表于8月24日出版的《物理评论快报》杂志。

量子引力的新曙光

量子引力主要就是尝试将量子力学与广义相对论合并在一起，描述对重力场进行量子化，属于万有理论之一隅。但应该如何结合，又如何让二者在微观长度等级下维持正确性，以及任何候选的量子引力论又能提供什么样可证实的预测，这是当前的物理学悬而未决的问题。遗憾的是，量子引力所探讨的能量与尺度，乃是此前实验室条件下无法观测得到的，尽管可能，且可以透过天文观测来检验，但仍属少数特例，关于量子引力理论发展上的提示一直未能成功。

点击阅读全文...

写在前面：本文是笔者数学建模课的作业，探讨了两生物种群竞争的常微分方程组模型的解的性质，展示了微分方程定性理论的基本思想。当然，本文最重要的目的，是展示LaTeX与Python的完美结合。（本文的图均由Python的Matplotlib模块生成；而文档则采用LaTeX编辑。）

问题提出

研究在同一个自然环境中生存的两个种群之间的竞争关系。假设两个种群独自在这个自然环境中生存时数量演变都服从Logistic规律，又假设当它们相互竞争时都会减慢对方数量的增长，增长速度的减小都与它们数量的乘积成正比。按照这样的假设建立的常微分方程模型为
$$\begin{equation}\label{eq:jingzhengfangcheng}\left\{\begin{aligned}\frac{dx_1}{dt}=r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2 \\
\frac{dx_2}{dt}=r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2\end{aligned}\right.\end{equation}$$
本文分别通过定量和定性两个角度来分析该方程的性质。

点击阅读全文...

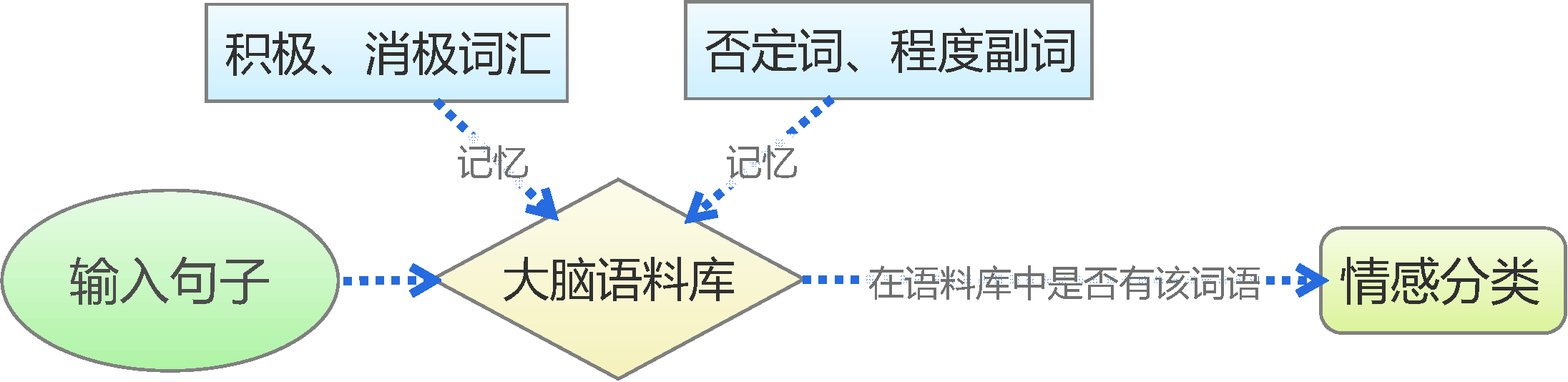
前言：四五月份的时候，我参加了两个数据挖掘相关的竞赛，分别是物电学院举办的“亮剑杯”，以及第三届 “泰迪杯”全国大学生数据挖掘竞赛。很碰巧的是，两个比赛中，都有一题主要涉及到中文情感分类工作。在做“亮剑杯”的时候，由于我还是初涉，水平有限，仅仅是基于传统的思路实现了一个简单的文本情感分类模型。而在后续的“泰迪杯”中，由于学习的深入，我已经基本了解深度学习的思想，并且用深度学习的算法实现了文本情感分类模型。因此，我打算将两个不同的模型都放到博客中，供读者参考。刚入门的读者，可以从中比较两者的不同，并且了解相关思路。高手请一笑置之。

基于情感词典

人的最简单的判断思维

点击阅读全文...

很多人觉得“模型”、“大数据”、“机器学习”这些字眼很高大很神秘，事实上，它跟我们生活中选水果差不了多少。本文用了几千字，来试图教会大家怎么选芒果...

模型的比喻

芒果

假如我要从一批芒果中，找出好吃的那个来。而我不能直接切开芒果尝尝，所以我只能观察芒果，能观察到的量有颜色、表面的气味、大小等等，这些就是我们能够收集到的信息（特征）。

生活中还要很多这样的例子，比如买火柴（可能年轻的城里人还没见过火柴？），如何判断一盒火柴的质量？难道要每根火柴都划划，看看着不着火？显然不行，我们最多也只能划几根，全部划了，火柴也不成火柴了。当然，我们还能看看火柴的样子，闻闻火柴的气味，这些动作是可以接受的。

点击阅读全文...

语言处理

在《文本情感分类（一）：传统模型》一文中，笔者简单介绍了进行文本情感分类的传统思路。传统的思路简单易懂，而且稳定性也比较强，然而存在着两个难以克服的局限性：一、精度问题，传统思路差强人意，当然一般的应用已经足够了，但是要进一步提高精度，却缺乏比较好的方法；二、背景知识问题，传统思路需要事先提取好情感词典，而这一步骤，往往需要人工操作才能保证准确率，换句话说，做这个事情的人，不仅仅要是数据挖掘专家，还需要语言学家，这个背景知识依赖性问题会阻碍着自然语言处理的进步。

点击阅读全文...

熵的概念

作为一名物理爱好者，我一直对统计力学中“熵”这个概念感到神秘和好奇。因此，当我接触数据科学的时候，我也对最大熵模型产生了浓厚的兴趣。

熵是什么？在通俗的介绍中，熵一般有两种解释：（1）熵是不确定性的度量；（2）熵是信息的度量。看上去说的不是一回事，其实它们说的就是同一个意思。首先，熵是不确定性的度量，它衡量着我们对某个事物的“无知程度”。熵为什么又是信息的度量呢？既然熵代表了我们对事物的无知，那么当我们从“无知”到“完全认识”这个过程中，就会获得一定的信息量，我们开始越无知，那么到达“完全认识”时，获得的信息量就越大，因此，作为不确定性的度量的熵，也可以看作是信息的度量，说准确点，是我们能从中获得的最大的信息量。

点击阅读全文...

上集回顾

在第一篇中，笔者介绍了“熵”这个概念，以及它的一些来龙去脉。熵的公式为
$$S=-\sum_x p(x)\log p(x)\tag{1}$$
或
$$S=-\int p(x)\log p(x) dx\tag{2}$$
并且在第一篇中，我们知道熵既代表了不确定性，又代表了信息量，事实上它们是同一个概念。

说完了熵这个概念，接下来要说的是“最大熵原理”。最大熵原理告诉我们，当我们想要得到一个随机事件的概率分布时，如果没有足够的信息能够完全确定这个概率分布（可能是不能确定什么分布，也可能是知道分布的类型，但是还有若干个参数没确定），那么最为“保险”的方案是选择使得熵最大的分布。

最大熵原理

承认我们的无知

很多文章在介绍最大熵原理的时候，会引用一句著名的句子——“不要把鸡蛋放在同一个篮子里”——来通俗地解释这个原理。然而，笔者窃以为这句话并没有抓住要点，并不能很好地体现最大熵原理的要义。笔者认为，对最大熵原理更恰当的解释是：承认我们的无知！

点击阅读全文...