也来盘点一些最近的非Transformer工作
By 苏剑林 | 2021-05-24 | 61463位读者 | 引用大家最近应该多多少少都被各种MLP相关的工作“席卷眼球”了。以Google为主的多个研究机构“奇招频出”,试图从多个维度“打击”Transformer模型,其中势头最猛的就是号称是纯MLP的一系列模型了,让人似乎有种“MLP is all you need”时代到来的感觉。
这一顿顿让人眼花缭乱的操作背后,究竟是大道至简下的“返璞归真”,还是江郎才尽后的“冷饭重炒”?让我们也来跟着这股热潮,一起盘点一些最近的相关工作。
五月人倍忙
怪事天天有,五月特别多。这个月以来,各大机构似乎相约好了一样,各种非Transformer的工作纷纷亮相,仿佛“忽如一夜春风来,千树万树梨花开”。单就笔者在Arxiv上刷到的相关论文,就已经多达七篇(一个月还没过完,七篇方向极其一致的论文),涵盖了NLP和CV等多个任务,真的让人应接不暇:
UniVAE:基于Transformer的单模型、多尺度的VAE模型
By 苏剑林 | 2021-06-29 | 73869位读者 | 引用多任务学习漫谈(三):分主次之序
By 苏剑林 | 2022-02-14 | 35863位读者 | 引用多任务学习是一个很宽泛的命题,不同场景下多任务学习的目标不尽相同。在《多任务学习漫谈(一):以损失之名》和《多任务学习漫谈(二):行梯度之事》中,我们将多任务学习的目标理解为“做好每一个任务”,具体表现是“尽量平等地处理每一个任务”,我们可以称之为“平行型多任务学习”。然而,并不是所有多任务学习的目标都是如此,在很多场景下,我们主要还是想学好某一个主任务,其余任务都只是辅助,希望通过增加其他任务的学习来提升主任务的效果罢了,此类场景我们可以称为“主次型多任务学习”。
在这个背景下,如果还是沿用平行型多任务学习的“做好每一个任务”的学习方案,那么就可能会明显降低主任务的效果了。所以本文继续沿着“行梯度之事”的想法,探索主次型多任务学习的训练方案。
目标形式
在这篇文章中,我们假设读者已经阅读并且基本理解《多任务学习漫谈(二):行梯度之事》里边的思想和方法,那么在梯度视角下,让某个损失函数保持下降的必要条件是更新量与其梯度夹角至少大于90度,这是贯穿全文的设计思想。
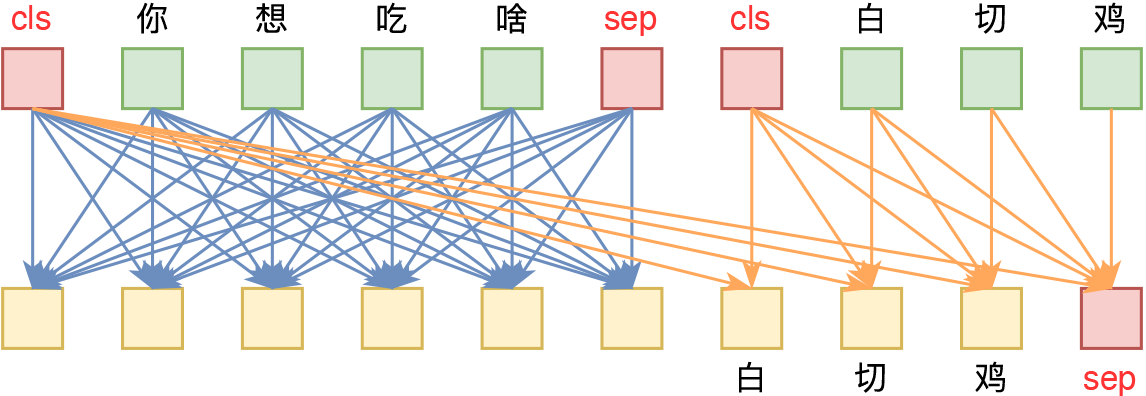
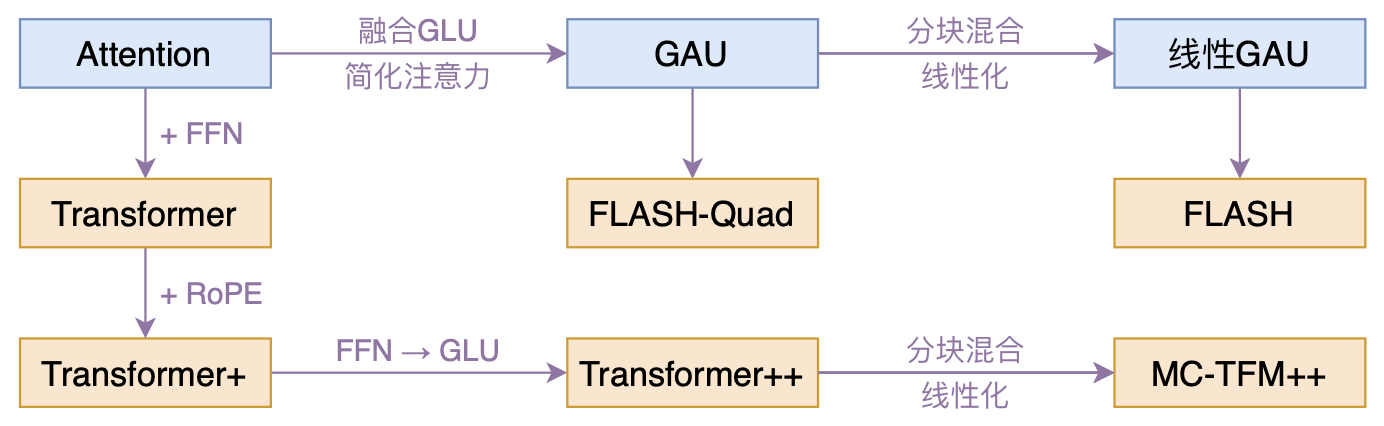
FLASH:可能是近来最有意思的高效Transformer设计
By 苏剑林 | 2022-02-25 | 180751位读者 | 引用高效Transformer,泛指所有概率Transformer效率的工作,笔者算是关注得比较早了,最早的博客可以追溯到2019年的《为节约而生:从标准Attention到稀疏Attention》,当时做这块的工作很少。后来,这类工作逐渐多了,笔者也跟进了一些,比如线性Attention、Performer、Nyströmformer,甚至自己也做了一些探索,比如之前的“Transformer升级之路”。再后来,相关工作越来越多,但大多都很无趣,所以笔者就没怎么关注了。
大抵是“久旱逢甘霖”的感觉,最近终于出现了一个比较有意思的高效Transformer工作——来自Google的《Transformer Quality in Linear Time》,经过细读之后,笔者认为论文里边真算得上是“惊喜满满”了~
生成扩散模型漫谈(二):DDPM = 自回归式VAE
By 苏剑林 | 2022-07-06 | 128802位读者 | 引用在文章《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中,我们为生成扩散模型DDPM构建了“拆楼-建楼”的通俗类比,并且借助该类比完整地推导了生成扩散模型DDPM的理论形式。在该文章中,我们还指出DDPM本质上已经不是传统的扩散模型了,它更多的是一个变分自编码器VAE,实际上DDPM的原论文中也是将它按照VAE的思路进行推导的。
所以,本文就从VAE的角度来重新介绍一版DDPM,同时分享一下自己的Keras实现代码和实践经验。
Github地址:https://github.com/bojone/Keras-DDPM
多步突破
在传统的VAE中,编码过程和生成过程都是一步到位的:
\begin{equation}\text{编码:}\,\,x\to z\,,\quad \text{生成:}\,\,z\to x\end{equation}
Muon优化器赏析:从向量到矩阵的本质跨越
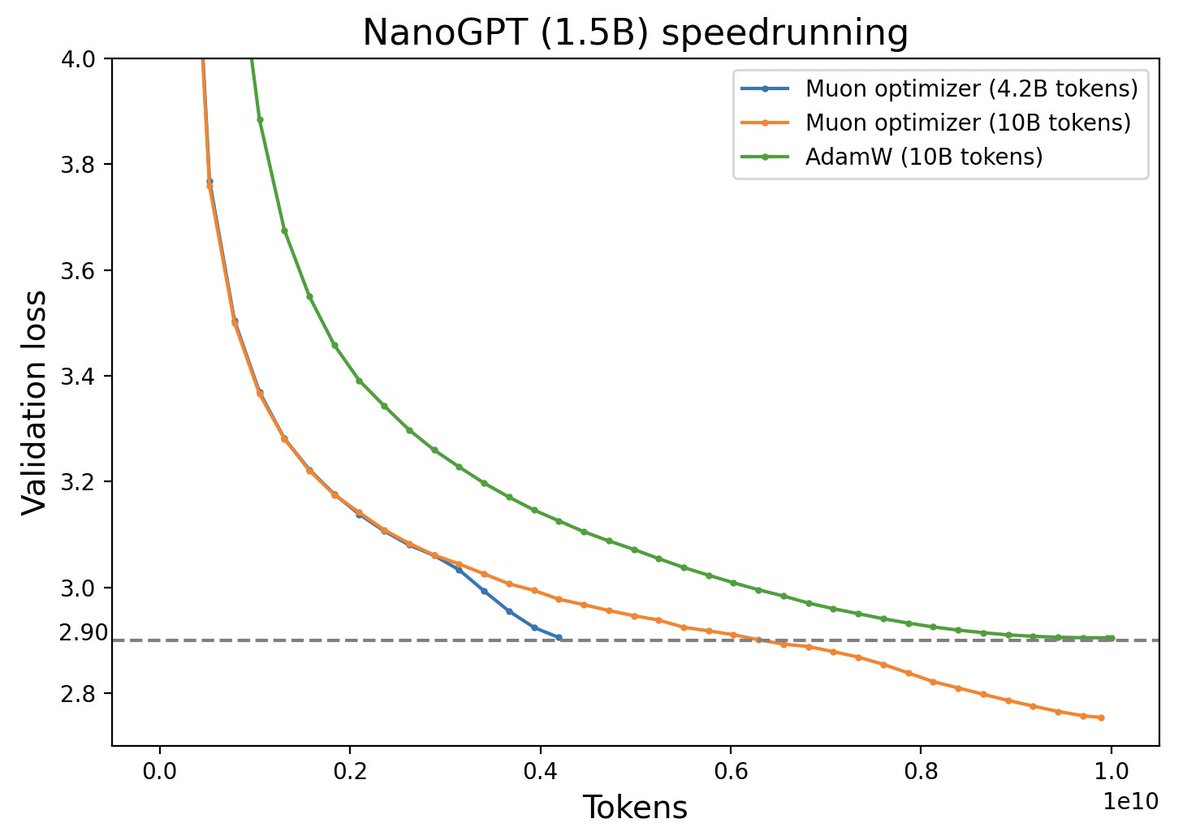
By 苏剑林 | 2024-12-10 | 7337位读者 | 引用随着LLM时代的到来,学术界对于优化器的研究热情似乎有所减退。这主要是因为目前主流的AdamW已经能够满足大多数需求,而如果对优化器“大动干戈”,那么需要巨大的验证成本。因此,当前优化器的变化,多数都只是工业界根据自己的训练经验来对AdamW打的一些小补丁。
不过,最近推特上一个名为“Muon”的优化器颇为热闹,它声称比AdamW更为高效,且并不只是在Adam基础上的“小打小闹”,而是体现了关于向量与矩阵差异的一些值得深思的原理。本文让我们一起赏析一番。
施密特系统的校正镜方程求解
By 苏剑林 | 2011-02-11 | 32645位读者 | 引用非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope
本文在牧夫天文论坛的讨论:
http://www.astronomy.ac/bbs/thread-160257-1-1.html
为了克服折射望远镜的色差问题,1670年,牛顿制造了第一台实用的反射式望远镜,将望远镜的主镜由玻璃透镜换成了抛物反射面,从而消除了色差。然而,相比球面镜,大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了,而抛物线每点的曲率并不相等,所以需要逐个磨制曲率不等的小镜片,并按照严格的顺序组合起来。这无疑大大增加了磨制难度。
为了解决这一难题,天文学家们想到了一个折衷的办法:以球面为主镜,并配以校正镜来校正球差。迎着这一思路,施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而,校正镜是一个比抛物面更加复杂的四次曲面,磨制工艺要求更高,因此,校正镜也不宜过大。
力学系统及其对偶性(三)
By 苏剑林 | 2013-11-15 | 17592位读者 | 引用在上一篇文章中,我已经初步地从最小作用量原理的角度来观察对偶定律的表现。虽然那是一种便捷有效的方法,但是还是给我们流下了一些遗憾。上一节是从几何形式的作用量原理出发的,而没有在一般形式的作用量框架下讨论。因为如果在$S=\int Ldt=\int (T-U)dt$的形式下讨论坐标变换问题会出现困难,困难源于我们进行了变换$d\tau=|z|^2 dt$,这导致了时间和空间的耦合,变分不能简单地进行。但是,这并非无法解决的问题。我们还是可以在基本的作用量原理之下讨论变换问题。下面将对此问题进行讨论。
变分中的变量代换
考虑一个一般的保守系统的作用量:
$$S=\int_{t_1}^{t_2} L(q,\frac{dq}{dt})dt$$









最近评论