科学空间|Scientific Spaces

记得科学空间刚开始的时候，没有什么原创的内容，有一段时间在翻译APOD的图片，后来渐渐地专注原创，就没有翻译了。这次再来分享一张图片，是兴隆山上的双子座流星雨，是国内爱好者Steed Yu拍摄的，被APOD收录。

兴隆山的双子座流星雨（来源：http://apod.nasa.gov/apod/ap151223.html）

点击阅读全文...

外微分

向量的外积一般只定义于不超过3维的空间。为了在更高维空间中使用反对称运算，我们需要下面描述的微分形式与外微分。

我们知道，任意$x$的函数的微分都可以写成$dx^{\mu}$的线性组合，在这里，各$dx^{\mu}$实则上扮演了一个基的角色，因此，我们不妨把$dx^{\mu}$看成是一组基，并且把任意函数称为微分0形式，而诸如$\omega_{\mu}dx^{\mu}$的式子，称为微分1形式。

在$dx^{\mu}$这组基之上，我们定义外积$\land$，即有反对称的运算$dx^{\mu}\land dx^{\nu}$，并且把诸如$\omega_{\mu\nu}dx^{\mu}\land dx^{\nu}$的式子，称为微分2形式。注意到这是$n$维空间中的外积，$dx^{\mu}\land dx^{\nu}$事实上是一个新空间的基，而不能用$dx^{\mu}$的线性组合来表示。

点击阅读全文...

证明下列级数发散或者收敛：
(1) $\sum_{x = 1}^\infty \frac{1}{x} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ...$
(2) $\sum_{x = 1}^\infty \frac{1}{x^2} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + ...$

一眼看上去，由于$1/x,1/{x^2}$都会趋向零，所以它们应该是收敛的。真的是这样吗？

点击阅读全文...

通过上一小节的小故事，我们已经能够基本了解最速降线的内容了，它就是要我们求出满足某一极值条件的一个未知函数，由于函数是未知的，因此这类问题被称为“泛分析”。其中还谈到，伯努利利用费马原理巧妙地得出了答案，那么我们现在就再次回顾历史，追寻伯努利的答案，并且寻找进一步的应用。

最速降线-1

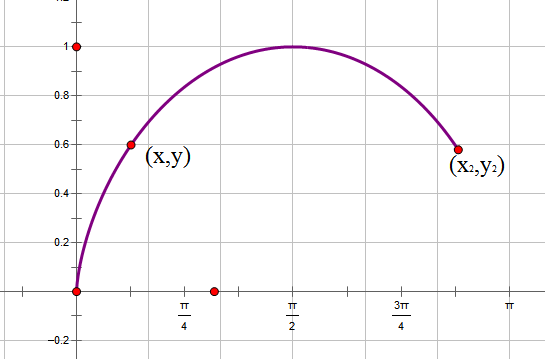
为了计算方便，我们把最速降线倒过来，把初始点设置在原点。在下落过程中，重力势能转化为动能，因此，在点(x,y)处有$\frac{1}{2} mv^2=mgy\Rightarrow v=\sqrt{2gy}$，由于纯粹为了探讨曲线形状，所以我们使g=0.5，即$v=\sqrt{y}$。在点(x,y)处所走的路程为$ds=\sqrt{dy^2+dx^2}=\sqrt{\dot{y}^2+1}dx$，所以时间为$dt=\frac{ds}{v}=\frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$，于是最速降线问题就是求使$t=\int_0^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$最小的函数。

点击阅读全文...

这几天潜水去了，和几个同学一起骑自行车游新兴（我们县），计划是去尽可能多的同学家。
所以网站这几天应该很少更新了，而且QQ上有人叫我可能不能及时回复，请见谅。^_^

点击阅读全文...

宇宙驿站维修期间，BoJone曾经想过用自己的电脑来搭建服务器，建立一个临时页面。但后来发现经常开着电脑不大好，就没有这样做了。不过如何在自己的电脑上搭建服务器，还是值得笔记一下的。

BoJone还在使用WinXP专业版系统，最标准的方法当然是使用IIS，可以一气呵成。但是考虑到IIS需要配置挺多东西的，所以就没有这样做了。所以自己在网上下载一些小软件，“拼凑”成了一个临时服务器。这样的方法也能够很方便地应用到各个Windows系统。

点击阅读全文...

正式直播活动计划于北京时间7月22日7时30分开始，11时30分结束，持续约4个小时。

（观看请安装PPlive插件，只能用IE或者IE内核浏览器观看）

简介：

点击阅读全文...

4000*4096，超高清，请等待图片下载，点击查看大图片

点击阅读全文...