Python的多进程编程技巧
By 苏剑林 | 2017-02-19 | 38685位读者 | 引用过程
在Python中,如果要多进程运算,一般是通过multiprocessing来实现的,常用的是multiprocessing中的进程池,比如:
from multiprocessing import Pool
import time
def f(x):
time.sleep(1)
print x+1
return x+1
a = range(10)
pool = Pool(4)
b = pool.map(f, a)
pool.close()
pool.join()
print b
这样写简明清晰,确实方便,有趣的是,只需要将multiprocessing换成multiprocessing.dummy,就可以将程序从多进程改为多线程了。
什么时候多进程的加速比可以大于1?
By 苏剑林 | 2019-10-27 | 59879位读者 | 引用多进程或者多线程等并行加速目前已经不是什么难事了,相信很多读者都体验过。一般来说,我们会有这样的结论:多进程的加速比很难达到1。换句话说,当你用10进程去并行跑一个任务时,一般只能获得不到10倍的加速,而且进程越多,这个加速比往往就越低。
要注意,我们刚才说“很难达到1”,说明我们的潜意识里就觉得加速比最多也就是1。理论上确实是的,难不成用10进程还能获得20倍的加速?这不是天上掉馅饼吗?不过我前几天确实碰到了一个加速比远大于1的例子,所以在这里跟大家分享一下。
词频统计
我的原始任务是统计词频:我有很多文章,然后我们要对这些文章进行分词,最后汇总出一个词频表出来。一般的写法是这样的:
tokens = {}
for text in read_texts():
for token in tokenize(text):
tokens[token] = tokens.get(token, 0) + 1这种写法在我统计THUCNews全部文章的词频时,大概花了20分钟。
将“Softmax+交叉熵”推广到多标签分类问题
By 苏剑林 | 2020-04-25 | 349768位读者 | 引用(注:本文的相关内容已整理成论文《ZLPR: A Novel Loss for Multi-label Classification》,如需引用可以直接引用英文论文,谢谢。)
一般来说,在处理常规的多分类问题时,我们会在模型的最后用一个全连接层输出每个类的分数,然后用softmax激活并用交叉熵作为损失函数。在这篇文章里,我们尝试将“Softmax+交叉熵”方案推广到多标签分类场景,希望能得到用于多标签分类任务的、不需要特别调整类权重和阈值的loss。
单标签到多标签
一般来说,多分类问题指的就是单标签分类问题,即从$n$个候选类别中选$1$个目标类别。假设各个类的得分分别为$s_1,s_2,
\dots,s_n$,目标类为$t\in\{1,2,\dots,n\}$,那么所用的loss为
\begin{equation}-\log \frac{e^{s_t}}{\sum\limits_{i=1}^n e^{s_i}}= - s_t + \log \sum\limits_{i=1}^n e^{s_i}\label{eq:log-softmax}\end{equation}
这个loss的优化方向是让目标类的得分$s_t$变为$s_1,s_2,\dots,s_t$中的最大值。关于softmax的相关内容,还可以参考《寻求一个光滑的最大值函数》、《函数光滑化杂谈:不可导函数的可导逼近》等文章。
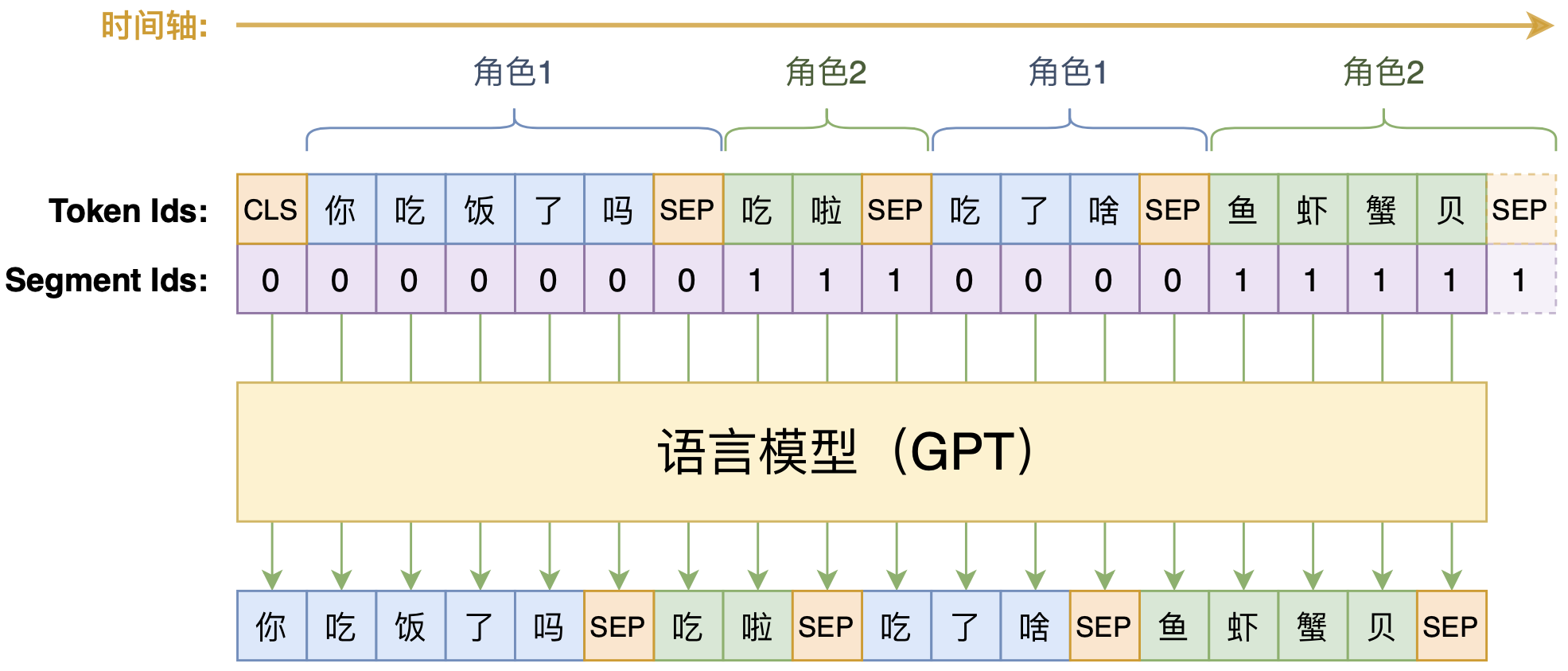
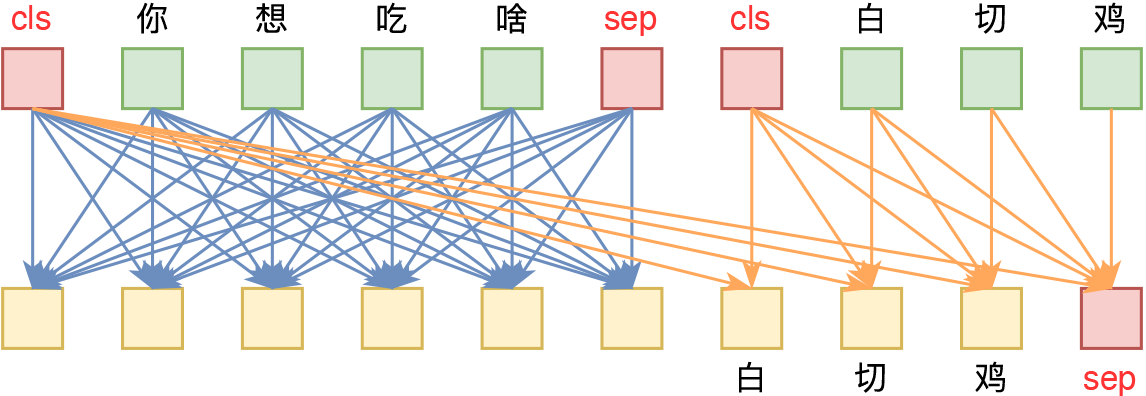
动手做个DialoGPT:基于LM的生成式多轮对话模型
By 苏剑林 | 2020-09-07 | 104714位读者 | 引用搜狐文本匹配:基于条件LayerNorm的多任务baseline
By 苏剑林 | 2021-04-16 | 90218位读者 | 引用前段时间看到了“2021搜狐校园文本匹配算法大赛”,觉得赛题颇有意思,便尝试了一下,不过由于比赛本身只是面向在校学生,所以笔者是不能作为正式参赛人员参赛的,因此把自己的做法开源出来,作为比赛baseline供大家参考。
赛题介绍
顾名思义,比赛的任务是文本匹配,即判断两个文本是否相似,本来是比较常规的任务,但有意思的是它分了多个子任务。具体来说,它分A、B两大类,A类匹配标准宽松一些,B类匹配标准严格一些,然后每个大类下又分为“短短匹配”、“短长匹配”、“长长匹配”3个小类,因此,虽然任务类型相同,但严格来看它是六个不同的子任务。
两个多元正态分布的KL散度、巴氏距离和W距离
By 苏剑林 | 2021-07-08 | 109048位读者 | 引用正态分布是最常见的连续型概率分布之一。它是给定均值和协方差后的最大熵分布(参考《“熵”不起:从熵、最大熵原理到最大熵模型(二)》),也可以看作任意连续型分布的二阶近似,它的地位就相当于一般函数的线性近似。从这个角度来看,正态分布算得上是最简单的连续型分布了。也正因为简单,所以对于很多估计量来说,它都能写出解析解来。
本文主要来计算两个多元正态分布的几种度量,包括KL散度、巴氏距离和W距离,它们都有显式解析解。
正态分布
这里简单回顾一下正态分布的一些基础知识。注意,仅仅是回顾,这还不足以作为正态分布的入门教程。
概率密度
正态分布,也即高斯分布,是定义在$\mathbb{R}^n$上的连续型概率分布,其概率密度函数为
\begin{equation}p(\boldsymbol{x})=\frac{1}{\sqrt{(2\pi)^n \det(\boldsymbol{\Sigma})}}\exp\left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}\end{equation}
UniVAE:基于Transformer的单模型、多尺度的VAE模型
By 苏剑林 | 2021-06-29 | 74178位读者 | 引用CoSENT(二):特征式匹配与交互式匹配有多大差距?
By 苏剑林 | 2022-01-12 | 90774位读者 | 引用一般来说,文本匹配有交互式(Interaction-based)和特征式(Representation-based)两种实现方案,其中交互式是指将两个文本拼接在一起当成单文本进行分类,而特征式则是指两个句子分别由编码器编码为句向量后再做简单的融合处理(算cos值或者接一个浅层网络)。通常的结论是,交互式由于使得两个文本能够进行充分的比较,所以它准确性通常较好,但明显的缺点是在检索场景的效率较差;而特征式则可以提前计算并缓存好句向量,所以它有着较高的效率,但由于句子间的交互程度较浅,所以通常效果不如交互式。
上一篇文章笔者介绍了CoSENT,它本质上也是一种特征式方案,并且相比以往的特征式方案效果有所提高。于是笔者的好胜心就上来了:CoSENT能比得过交互式吗?特征式相比交互式的差距有多远呢?本文就来做个比较。
自动阈值
在文章《CoSENT(一):比Sentence-BERT更有效的句向量方案》中,我们评测CoSENT所用的指标是Spearman系数,它是一个只依赖于预测结果相对顺序的指标,不依赖于阈值,比较适合检索场景的评测。但如果评测指标是accuracy或者F1这些分类指标,则必须确定一个阈值,将预测结果大于这个数的预测结果视为正、小于则为负,然后才能计算指标。在二分类的场景,我们用二分法就可以有效地确定这个阈值。









最近评论