科学空间|Scientific Spaces

继续“让Keras更酷一些”之旅。

今天我们会用Keras实现灵活地输出任意中间变量，还有无缝地进行权重滑动平均，最后顺便介绍一下生成器的进程安全写法。

首先是输出中间变量。在自定义层时，我们可能希望查看中间变量，这些需求有些是比较容易实现的，比如查看中间某个层的输出，只需要将截止到这个层的部分模型保存为一个新模型即可，但有些需求是比较困难的，比如在使用Attention层时我们可能希望查看那个Attention矩阵的值，如果用构建新模型的方法则会非常麻烦。而本文则给出一种简单的方法，彻底满足这个需求。

接着是权重滑动平均。权重滑动平均是稳定、加速模型训练甚至提升模型效果的一种有效方法，很多大型模型（尤其是GAN）几乎都用到了权重滑动平均。一般来说权重滑动平均是作为优化器的一部分，所以一般需要重写优化器才能实现它。本文介绍一个权重滑动平均的实现，它可以无缝插入到任意Keras模型中，不需要自定义优化器。

至于生成器的进程安全写法，则是因为Keras读取生成器的时候，用到了多进程，如果生成器本身也包含了一些多进程操作，那么可能就会导致异常，所以需要解决这个这个问题。

点击阅读全文...

在对GAN的学习和思考过程中，我发现我不仅学习到了一种有效的生成模型，而且它全面地促进了我对各种模型各方面的理解，比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”，而是具有深刻意义的概率模型和推断方法。

作为事后的总结，我觉得对GAN的理解可以粗糙地分为三个阶段：

1、样本阶段：在这个阶段中，我们了解了GAN的“鉴别者-造假者”诠释，懂得从这个原理出发来写出基本的GAN公式（如原始GAN、LSGAN），比如判别器和生成器的loss，并且完成简单GAN的训练；同时，我们知道GAN有能力让图片更“真”，利用这个特性可以把GAN嵌入到一些综合模型中。

2、分布阶段：在这个阶段中，我们会从概率分布及其散度的视角来分析GAN，典型的例子是WGAN和f-GAN，同时能基本理解GAN的训练困难问题，比如梯度消失和mode collapse等，甚至能基本地了解变分推断，懂得自己写出一些概率散度，继而构造一些新的GAN形式。

3、动力学阶段：在这个阶段中，我们开始结合优化器来分析GAN的收敛过程，试图了解GAN是否能真的达到理论的均衡点，进而理解GAN的loss和正则项等因素如何影响的收敛过程，由此可以针对性地提出一些训练策略，引导GAN模型到达理论均衡点，从而提高GAN的效果。

点击阅读全文...

昨天刷arxiv时发现了一篇来自星星韩国的论文，名字很直白，就叫做《A Simple yet Effective Way for Improving the Performance of GANs》。打开一看，发现内容也很简练，就是提出了一种加强GAN的判别器的方法，能让GAN的生成指标有一定的提升。

作者把这个方法叫做Cascading Rejection，我不知道咋翻译，扔到百度翻译里边显示“级联抑制”，想想看好像是有这么点味道，就暂时这样叫着了。介绍这个方法倒不是因为它有多强大，而是觉得它的几何意义很有趣，而且似乎有一定的启发性。

正交分解

GAN的判别器一般是经过多层卷积后，通过flatten或pool得到一个固定长度的向量$\boldsymbol{v}$，然后再与一个权重向量$\boldsymbol{w}$做内积，得到一个标量打分（先不考虑偏置项和激活函数等末节）：
\begin{equation}D(\boldsymbol{x})=\langle \boldsymbol{v},\boldsymbol{w}\rangle\end{equation}
也就是说，用$\boldsymbol{v}$作为输入图片的表征，然后通过$\boldsymbol{v}$和$\boldsymbol{w}$的内积大小来判断出这个图片的“真”的程度。

点击阅读全文...

前些天刷Arxiv看到新文章《Self-Orthogonality Module: A Network Architecture Plug-in for Learning Orthogonal Filters》（下面简称“原论文”），看上去似乎有点意思，于是阅读了一番，读完确实有些收获，在此记录分享一下。

给全连接或者卷积模型的核加上带有正交化倾向的正则项，是不少模型的需求，比如大名鼎鼎的BigGAN就加入了类似的正则项。而这篇论文则引入了一个新的正则项，笔者认为整个分析过程颇为有趣，可以一读。

为什么希望正交？

在开始之前，我们先约定：本文所出现的所有一维向量都代表列向量。那么，现在假设有一个$d$维的输入样本$\boldsymbol{x}\in \mathbb{R}^d$，经过全连接或卷积层时，其核心运算就是：
\begin{equation}\boldsymbol{y}^{\top}=\boldsymbol{x}^{\top}\boldsymbol{W},\quad \boldsymbol{W}\triangleq (\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k)\label{eq:k}\end{equation}
其中$\boldsymbol{W}\in \mathbb{R}^{d\times k}$是一个矩阵，它就被称“核”（全连接核／卷积核），而$\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k\in \mathbb{R}^{d}$是该矩阵的各个列向量。

点击阅读全文...

本文的模型在ImageNet(128x128)上的条件生成效果

今天要介绍的结果还是跟能量模型相关，来自论文《Implicit Generation and Generalization in Energy-Based Models》。当然，它已经跟GAN没有什么关系了，但是跟本系列第二篇所介绍的能量模型关系较大，所以还是把它放到这个系列好了。

我当初留意到这篇论文，是因为机器之心的报导《MIT本科学神重启基于能量的生成模型，新框架堪比GAN》，但是说实在的，这篇文章没什么意思，说句不中听的，就是炒冷饭系列，媒体的标题也算中肯，是“重启”。这篇文章就是指出能量模型实际上就是某个特定的Langevin方程的静态解，然后就用这个Langevin方程来实现采样，有了采样过程也就可以完成能量模型的训练，这些理论都是现成的，所以这个过程我在学习随机微分方程的时候都想过，我相信很多人也都想过。因此，我觉得作者的贡献就是把这个直白的想法通过一系列炼丹技巧实现了。

但不管怎样，能训练出来也是一件很不错的事情，另外对于之前没了解过相关内容的读者来说，这确实也算是一个不错的能量模型案例，所以我论文的整体思路整理一下，让读者能够更全面地理解能量模型。

点击阅读全文...

一般来说，神经网络处理的东西都是连续的浮点数，标准的输出也是连续型的数字。但实际问题中，我们很多时候都需要一个离散的结果，比如分类问题中我们希望输出正确的类别，“类别”是离散的，“类别的概率”才是连续的；又比如我们很多任务的评测指标实际上都是离散的，比如分类问题的正确率和F1、机器翻译中的BLEU，等等。

还是以分类问题为例，常见的评测指标是正确率，而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联，但它们不是绝对的单调相关关系。换句话说，交叉熵下降了，正确率不一定上升。显然，如果能用正确率的相反数做损失函数，那是最理想的，但正确率是不可导的（涉及到$\text{argmax}$等操作），所以没法直接用。

这时候一般有两种解决方案；一是动用强化学习，将正确率设为奖励函数，这是“用牛刀杀鸡”的方案；另外一种是试图给正确率找一个光滑可导的近似公式。本文就来探讨一下常见的不可导函数的光滑近似，有时候我们称之为“光滑化”，有时候我们也称之为“软化”。

max

后面谈到的大部分内容，基础点就是$\max$操作的光滑近似，我们有：
\begin{equation}\max(x_1,x_2,\dots,x_n) = \lim_{K\to +\infty}\frac{1}{K}\log\left(\sum_{i=1}^n e^{K x_i}\right)\end{equation}

点击阅读全文...

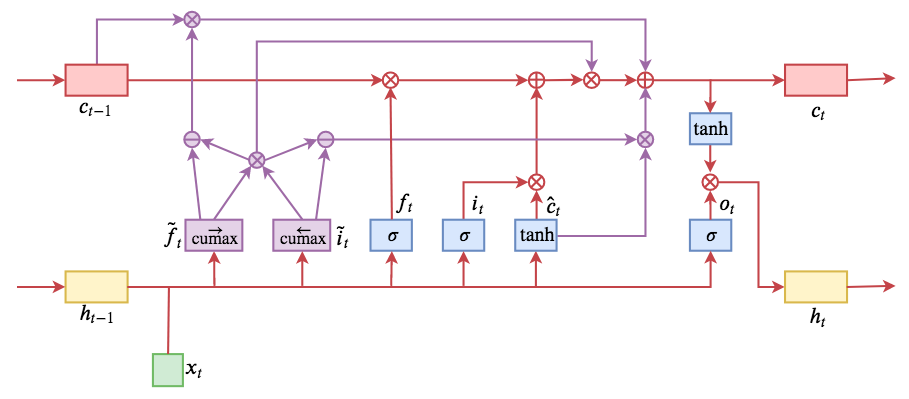
今天介绍一个有意思的LSTM变种：ON-LSTM，其中“ON”的全称是“Ordered Neurons”，即有序神经元，换句话说这种LSTM内部的神经元是经过特定排序的，从而能够表达更丰富的信息。ON-LSTM来自文章《Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks》，顾名思义，将神经元经过特定排序是为了将层级结构（树结构）整合到LSTM中去，从而允许LSTM能自动学习到层级结构信息。这篇论文还有另一个身份：ICLR 2019的两篇最佳论文之一，这表明在神经网络中融合层级结构（而不是纯粹简单地全向链接）是很多学者共同感兴趣的课题。

ON-LSTM运算流程示意图。主要是将分段函数用cumax光滑化变成可导。

笔者留意到ON-LSTM是因为机器之心的介绍，里边提到它除了提高了语言模型的效果之外，甚至还可以无监督地学习到句子的句法结构！正是这一点特性深深吸引了我，而它最近获得ICLR 2019最佳论文的认可，更是坚定了我要弄懂它的决心。认真研读、推导了差不多一星期之后，终于有点眉目了，遂写下此文。

在正式介绍ON-LSTM之后，我忍不住要先吐槽一下这篇文章实在是写得太差了，将一个明明很生动形象的设计，讲得异常晦涩难懂，其中的核心是$\tilde{f}_t$和$\tilde{i}_t$的定义，文中几乎没有任何铺垫就贴了出来，也没有多少诠释，开始的读了好几次仍然像天书一样...总之，文章写法实在不敢恭维～

点击阅读全文...

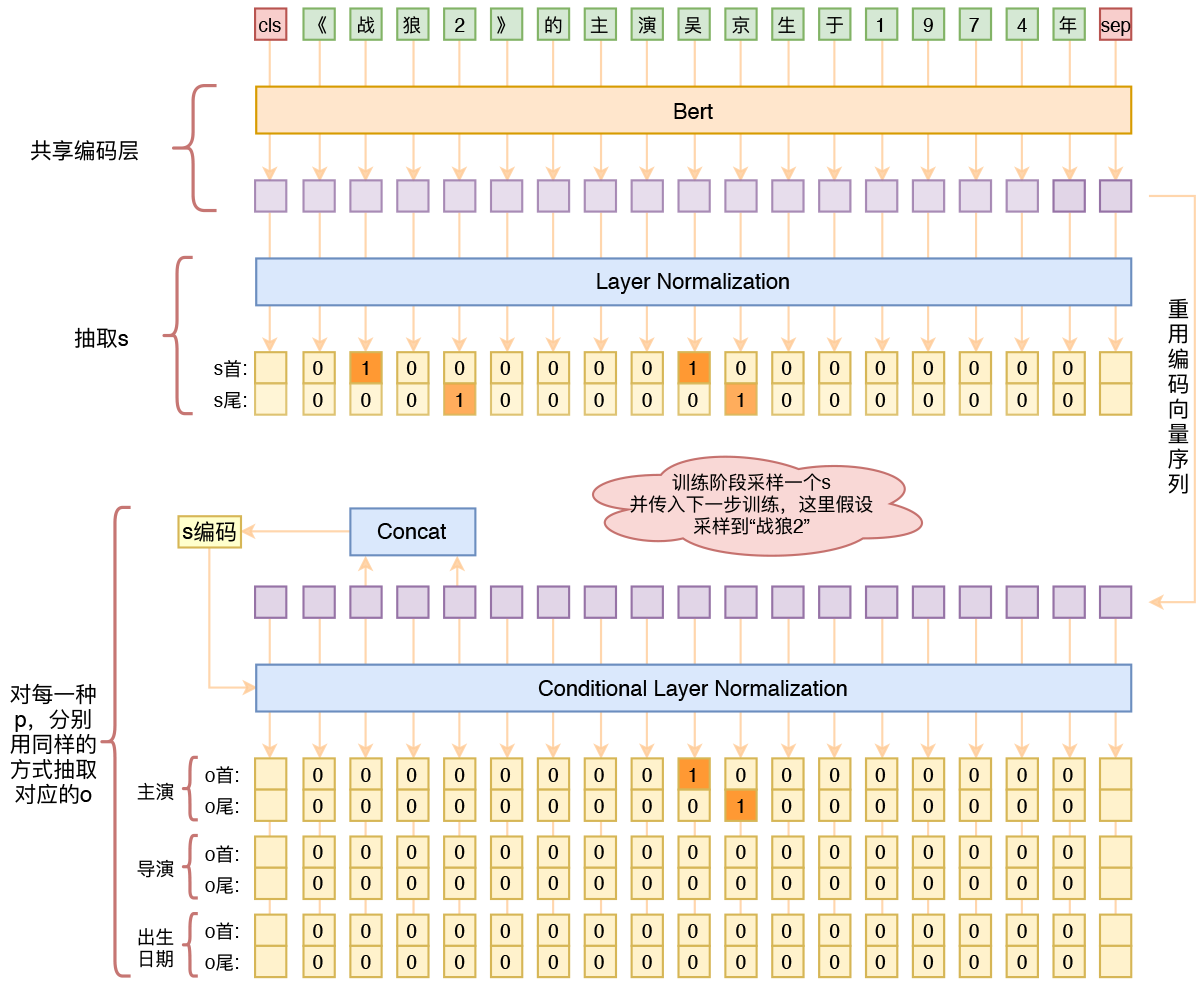
在开发bert4keras的时候就承诺过，会逐渐将之前用keras-bert实现的例子逐渐迁移到bert4keras来，而那里其中一个例子便是三元组抽取的任务。现在bert4keras的例子已经颇为丰富了，但还没有序列标注和信息抽取相关的任务，而三元组抽取正好是这样的一个任务，因此就补充上去了。

基于Bert的三元组抽取模型结构示意图

点击阅读全文...