包含关键字变形梯度的时间导数的文章

27 Feb

【NASA每日一图】黎明天空中的奋进号太空梭

By 苏剑林 | 2010-02-27 | 41109位读者 | 引用

图片说明：黎明天空中的奋进号太空梭，版权：Malcolm Park

分类：图片摄影标签：国际空间站, 航天飞机阅读全文 4 评论

2 May

前几天做到了一道不等式题目，求2a-b的值域。其中
$1 < a + b < 2\tag{1}$ $-2 < a - b < -1\tag{2}$
老师很高兴地把两式左右两边加起来，得到 $-1<2a<1$ ；然后把第二式乘以(-1)，得到 $1 < b - a < 2$ ，然后再与(1)相加，得到 $2 < 2 b< 4 \Rightarrow 1 < b < 2$ ；接着把这式子乘上(-1)，然后与 $-1<2a<1$ 相加。于是结果很显然， $-3<2a-b<0$ 。读者们，你们觉得这做法有问题吗？

点击阅读全文...

分类：数学研究标签：不等式阅读全文 6 评论

29 May

数学魔术——漂亮的近似

By 苏剑林 | 2010-05-29 | 38585位读者 | 引用

$e\approx\Big(1+3^{-2^{85}}\Big)^{9^{4^{6\times 7}}}$

这个e的近似表达很漂亮，它恰好用到了1到9这9个数字。而且漂亮的不仅仅是这一点，大家猜猜看它的有效数字是多少位？10 位？100 位？1000 位？10000 位？

点击阅读全文...

分类：数学研究标签：无理数, 近似阅读全文 5 评论

24 Jul

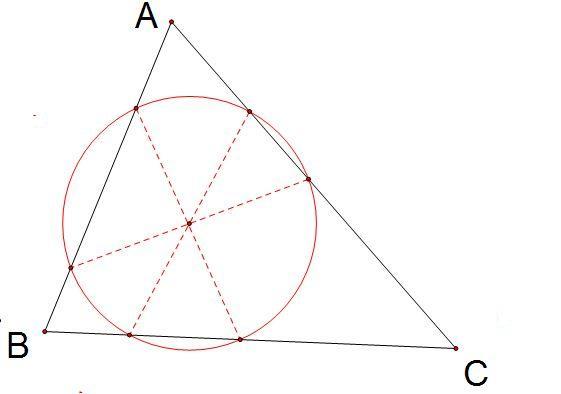
神秘的圆——三角形的“六接圆”(添加新方法)

By 苏剑林 | 2010-07-24 | 36149位读者 | 引用

数联天地论坛中的watt5151朋友提出了这样的一个问题：

三角形的“六接圆”

如图，已知三角形ABC，如何做一个圆，它与三角形三边都相交，而且六个交点可以连成三条直径？

点击阅读全文...

分类：数学研究标签：尺规作图, 圆, 三角形, 共线阅读全文 3 评论

27 Jun

威力巨大的“有向线段”

By 苏剑林 | 2010-06-27 | 22359位读者 | 引用

向量

向量，又称矢量，定义为线性空间中需要大小和方向才能完整表示的一个量。而对于我们来说，还是使用最简单的概念比较合适：向量就是“有向线段”。向量这一概念，来源于物理，而又不仅仅应用于物理。向量的出现，使得几何学和物理学的发展又多了一个强有力的工具，记得有一句这样的话：“对数的出现，延长了天文学家的寿命。”而我可以毫不夸张地说，向量的发展，也在不断地延长着数学家和物理学家的寿命！

点击阅读全文...

分类：数学研究标签：向量, 矢量, 几何阅读全文抢沙发

19 Jul

太阳中心的压强和温度

By 苏剑林 | 2010-07-19 | 35351位读者 | 引用

太阳

为了准备IOAA，同时也加深对天体物理的理解，所以就系统地学习一下天体物理学了。今天看到“太阳”这一章，并由此简单估算了一下太阳的中心压强和温度。

天体物理学给出了关于恒星结构的一些方程。假设存在一颗各项同性的球形恒星，则有
$\frac{dm(r)}{dr}=4\pi r^2 \rho(r)$ ————质量方程
其中m(r)是与恒星球心距离为r的一个球形区域内的总质量， $\rho(r)$ 是距离球心r处的物质的密度。我们也可以写成积分的形式
$m(r)=\int_0^R 4\pi r^2 \rho(r)dr$
其中R是恒星半径。这个方程的意思其实就是每一个壳层的质量叠加，所以就不详细推导了。