16
Oct
以自然数幂为系数的幂级数
By 苏剑林 | 2010-10-16 | 31393位读者 | 引用$\sum_{i=0}^{\infty} a_i x^i=a_0+a_1 x+a_2 x^2+a_3 x^3+...$
最近为了数学竞赛，我研究了有关数列和排列组合的相关问题。由于我讨厌为某个问题而设计专门的技巧，所以我偏爱通用的方法，哪怕过程相对麻烦。因此，我对数学归纳法（递推法）和生成函数法情有独钟。前者只需要列出问题的递归关系，而不用具体分析，最终把问题转移到解函数方程上来。后者则巧妙地把数列${a_n}$与幂级数$\sum_{i=0}^{\infty} a_i x^i$一一对应，巧妙地通过代数运算或微积分运算等得到结果。这里我们不用考虑该级数的敛散性，只需要知道它对应着哪一个“母函数”（母函数展开泰勒级数后得到了级数$\sum_{i=0}^{\infty} a_i x^i$）。显然，这两种方法的最终，都是把问题归结为代数问题。
23
Oct
科学空间：2010年11月重要天象
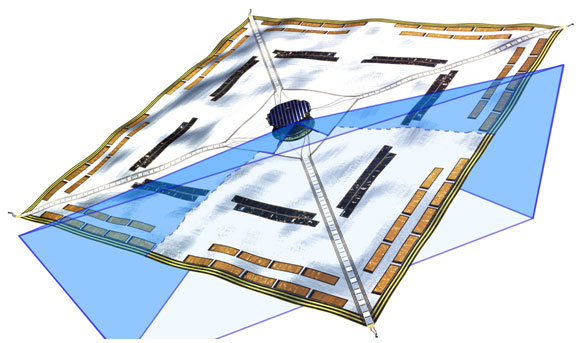
By 苏剑林 | 2010-10-23 | 21523位读者 | 引用
24
Oct
太阳帆技术的粗浅分析
By 苏剑林 | 2010-10-24 | 36857位读者 | 引用
27
Nov
《自然极值》系列——2.费马原理
By 苏剑林 | 2010-11-27 | 42851位读者 | 引用物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现，很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是费马原理，它指出了光的传播路径的一个重要规律：光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下费马原理。
费马原理俗称“最快到达原理”、“最小时间原理”。1657年，费马提出：
从P点到达Q点，在所有可行的路径中，光选择了所需时间最短的一条。
从P点到达Q点，在所有可行的路径中，光选择了所需时间为极值的一条。
这是一个极其奇妙的原理，也是自然界中最神奇的极值之一。作为非生物的光，居然自主地选择了最优路径，成为世界上“效率最高”的东西，这让人不得不佩服宇宙的伟大。这究竟是造物者的精心设计，还是无心之作？
10
Dec
《自然极值》系列——6.最速降线的解答
By 苏剑林 | 2010-12-10 | 62171位读者 | 引用通过上一小节的小故事，我们已经能够基本了解最速降线的内容了，它就是要我们求出满足某一极值条件的一个未知函数，由于函数是未知的，因此这类问题被称为“泛分析”。其中还谈到，伯努利利用费马原理巧妙地得出了答案，那么我们现在就再次回顾历史，追寻伯努利的答案，并且寻找进一步的应用。
最速降线-1
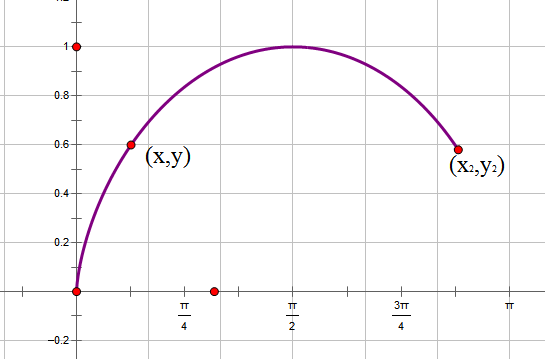
为了计算方便，我们把最速降线倒过来，把初始点设置在原点。在下落过程中，重力势能转化为动能，因此，在点(x,y)处有$\frac{1}{2} mv^2=mgy\Rightarrow v=\sqrt{2gy}$，由于纯粹为了探讨曲线形状，所以我们使g=0.5，即$v=\sqrt{y}$。在点(x,y)处所走的路程为$ds=\sqrt{dy^2+dx^2}=\sqrt{\dot{y}^2+1}dx$，所以时间为$dt=\frac{ds}{v}=\frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$，于是最速降线问题就是求使$t=\int_0^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$最小的函数。
9
Jan
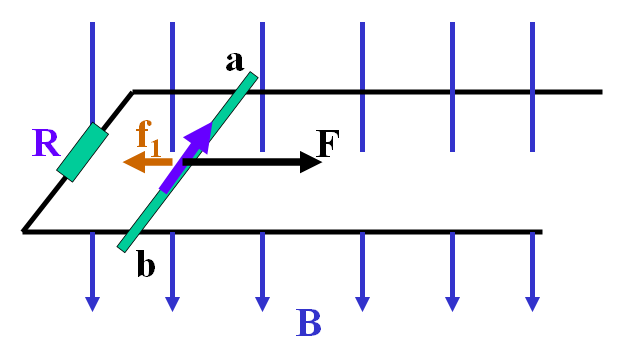
不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 42522位读者 | 引用
3
Feb
[SETI-50周年]茫茫宇宙觅知音
By 苏剑林 | 2011-02-03 | 19928位读者 | 引用转载自2011年1月的《天文爱好者》 作者：薛国轩
“多萝西计划”再探地外文明
据美国空间网站2010年11月13日报道，在人类“探索地外文明”（英文缩写为SETI）50周年纪念之际，世界多个国家的天文学家从本月起再度展开“且听外星人”的联合行动，以延续开始于1960年的“奥兹玛计划”。新的探索活动被命名为“多萝西计划”（Project Dorothy），已于11月5日正式启动，将持续整整一个月时间，来自澳大利亚、日本、韩国、意大利、荷兰、法国、阿根廷和美国的天文学家参与其中。他们将把大大小小的望远镜指向地球周围的一些星球，以期收听到外星人的“天外来音”。
Allen Telescope Array
最近评论