宇宙驿站服务器升级完毕
By 苏剑林 | 2014-01-19 | 31042位读者 | 引用视频演示:费曼的茶杯
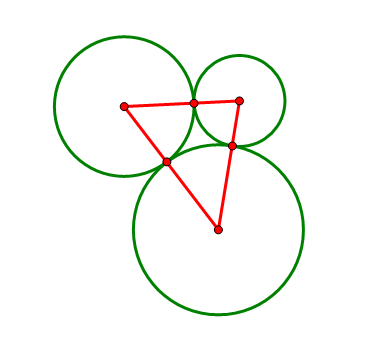
By 苏剑林 | 2014-02-07 | 18882位读者 | 引用在学车的时候,我堂大哥曾问我一道作圆的问题:
平面上给出三个两两相切的圆以及它们的圆心,求作一个圆与这三个圆都相切(尺规作图)。
如果从纯几何的途径入手,我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目,于是很快想到一个名词:反演。反演可以将圆反演成直线(圆过反演点),也可以将圆反演成圆(圆不过反演点),而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演,就变回原来的图形。本题的难点在于圆太多,利用反演,我们可以将它变为两条直线和一个圆的问题。
假设读者已经有了反演的基本知识,如果没有,请到
http://zh.wikipedia.org/wiki/反演
阅读相关内容。
三个相切圆的公切圆:补充
By 苏剑林 | 2014-01-30 | 26660位读者 | 引用线性微分方程组:已知特解求通解
By 苏剑林 | 2014-06-18 | 37521位读者 | 引用含有$n$个一阶常微分方程的一阶常微分方程组
$$\dot{\boldsymbol{x}}=\boldsymbol{A}\boldsymbol{x}$$
其中$\boldsymbol{x}=(x_1(t),\dots,x_n(t))^{T}$为待求函数,而$\boldsymbol{A}=(a_{ij}(t))_{n\times n}$为已知的函数矩阵。现在已知该方程组的$n-1$个线性无关的特解$\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_{n-1}$(解的列向量),求方程的通解。
这是我的一位同学在6月5号问我的一道题目,我当时看了一下,感觉可以通过李对称的方法很容易把解构造出来,当晚就简单分析了一下,发现根据李对称的思想,由上面已知的信息确实足以把通解构造出来。但是我尝试了好几天,尝试了几何、代数等思想,都没有很好地构造出相应的正则变量出来,从而也没有写出它的显式解,于是就搁置下来了。今天再分析这道题目时,竟在无意之间构造出了让我比较满意的解来~
翻到新的维度,把积分解决!
By 苏剑林 | 2014-02-25 | 37383位读者 | 引用一般来说,如果原函数容易找到的话,牛顿-莱布尼兹公式是定积分的通用方法。但是牛顿-莱布尼兹公式只适合连续函数的积分,如果积分区间含有奇点,那就不成立了。比如,我们考虑积分
$$\int_{-1}^1 \frac{1}{x^2}dx$$
当然,从严格的数学上来说,这种写法是不成立的,因为被积函数在原点没有意义。当然,从物理的角度来考虑,由于对称性,我们确信
$$\int_{-1}^1 \frac{1}{x^2}dx=2\int_{0}^1 \frac{1}{x^2}dx=\lim_{\varepsilon\to 0}2\int_{\varepsilon}^1 \frac{1}{x^2}dx$$
从而得出积分发散的结论。这种处理某种程度上是可以接受的,但是却不是让人满意的,因为它导致了分段。有什么办法可以直接处理这种情况呢?确实有的,同样引入参数,并且最终让参数为0,考虑带参数的积分
$$\int_{-1}^1 \frac{1}{x^2+\varepsilon^2}dx$$
只要参数为正,这个被积函数就在$\mathbb{R}$上处处连续了,也就是奇点消失了,这样子就可以用牛顿-莱布尼兹公式了
$$\int_{-1}^1 \frac{1}{x^2+\varepsilon^2}dx=\left.\frac{1}{\varepsilon}\arctan\left(\frac{x}{\varepsilon}\right)\right|_{-1}^{1}$$
考虑$\varepsilon\to 0$的情况,就自动得到了积分发散的结论。
不求珍馐百味,但愿开水白菜
By 苏剑林 | 2014-03-15 | 40301位读者 | 引用Mathieu方程
在文章《有质动力:倒立单摆的稳定性》中,我们分析了通过高频低幅振荡来使得倒立单摆稳定的可能性,并且得出了运动方程
$$l\ddot{\theta}+[h_0 \omega^2 \cos(\omega t)-g]\sin\theta=0$$
由此对单摆频率的下限提出了要求$\omega \gg \sqrt{\frac{g}{h_0}}$。然而,那个下限只不过是必要的,却不是充分的。如果要完整地分析该单摆的运动方程,最理想的方法当然是写出上述常微分方程的解析解。不过很遗憾,我们并没有办法做到这一点。我们只能够采取各种近似方法来求解。近似方法一般指数值计算方法,然后笔者偏爱的是解析方法,也就是说,即使是近似解,也希望能够求出近似的解析解。









最近评论