科学空间|Scientific Spaces

众所周知，LoRA是一种常见的参数高效的微调方法，我们在《梯度视角下的LoRA：简介、分析、猜测及推广》做过简单介绍。LoRA利用低秩分解来降低微调参数量，节省微调显存，同时训练好的权重可以合并到原始权重上，推理架构不需要作出改变，是一种训练和推理都比较友好的微调方案。此外，我们在《配置不同的学习率，LoRA还能再涨一点？》还讨论过LoRA的不对称性，指出给$A,B$设置不同的学习率能取得更好的效果，该结论被称为“LoRA+”。

为了进一步提升效果，研究人员还提出了不少其他LoRA变体，如AdaLoRA、rsLoRA、DoRA、PiSSA等，这些改动都有一定道理，但没有特别让人深刻的地方觉。然而，前两天的《LoRA-GA: Low-Rank Adaptation with Gradient Approximation》，却让笔者眼前一亮，仅扫了摘要就有种必然有效的感觉，仔细阅读后更觉得它是至今最精彩的LoRA改进。

究竟怎么个精彩法？LoRA-GA的实际含金量如何？我们一起来学习一下。

点击阅读全文...

在矩阵压缩这个问题上，我们通常有两个策略可以选择，分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸，而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的，那么相应地寻找矩阵稀疏近似的算法又是什么呢？

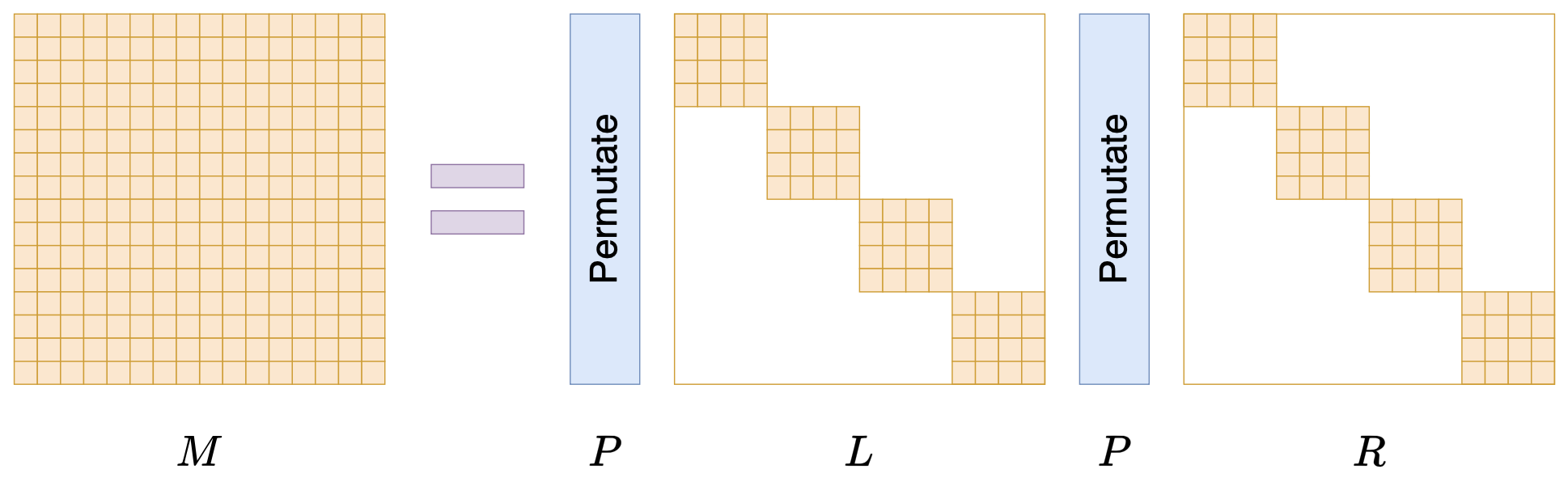
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》，它为上述问题给出了一个答案——“Monarch矩阵”，这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵，同时具备计算高效且表达能力强的特点，论文还讨论了如何求一般矩阵的Monarch近似，以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。

Monarch矩阵形式M=PLPR

值得指出的是，该论文的作者也正是著名的Flash Attention的作者Tri Dao，其工作几乎都在致力于改进LLM的性能，这篇Monarch也是他主页上特意展示的几篇论文之一，单从这一点看就非常值得学习一番。

点击阅读全文...

Softmax，顾名思义是“soft的max”，是$\max$算子（准确来说是$\text{argmax}$）的光滑近似，它通过指数归一化将任意向量$\boldsymbol{x}\in\mathbb{R}^n$转化为分量非负且和为1的新向量，并允许我们通过温度参数来调节它与$\text{argmax}$（的one hot形式）的近似程度。除了指数归一化外，我们此前在《通向概率分布之路：盘点Softmax及其替代品》也介绍过其他一些能实现相同效果的方案。

我们知道，最大值通常又称Top-1，它的光滑近似方案看起来已经相当成熟，那读者有没有思考过，一般的Top-$k$的光滑近似又是怎么样的呢？下面让我们一起来探讨一下这个问题。

问题描述

设向量$\boldsymbol{x}=(x_1,x_2,\cdots,x_n)\in\mathbb{R}^n$，简单起见我们假设它们两两不相等，即$i\neq j \Leftrightarrow x_i\neq x_j$。记$\Omega_k(\boldsymbol{x})$为$\boldsymbol{x}$最大的$k$个分量的下标集合，即$|\Omega_k(\boldsymbol{x})|=k$以及$\forall i\in \Omega_k(\boldsymbol{x}), j \not\in \Omega_k(\boldsymbol{x})\Rightarrow x_i > x_j$。我们定义Top-$k$算子$\mathcal{T}_k$为$\mathbb{R}^n\mapsto\{0,1\}^n$的映射：
$$\begin{equation} [\mathcal{T}_k(\boldsymbol{x})]_i = \left\{\begin{aligned}1,\,\, i\in \Omega_k(\boldsymbol{x}) \\ 0,\,\, i \not\in \Omega_k(\boldsymbol{x})\end{aligned}\right. \end{equation}$$
说白了，如果$x_i$属于最大的$k$个元素之一，那么对应的位置变成1，否则变成0，最终结果是一个Multi-Hot向量，比如$\mathcal{T}_2([3,2,1,4]) = [1,0,0,1]$。

点击阅读全文...

很早之前，就有读者提出希望把Cool Papers上面的数学公式渲染一下，因为很多偏数学的论文，它们的摘要甚至标题上都带有LaTeX代码写的数学公式，如果不把这些公式渲染出来，那么看上去就像是一堆乱码，确实会比较影响阅读体验。然而，之前的测试显示，负责渲染公式的MathJax跟谷歌翻译和延时加载都不大兼容，所以尽管需求存在已久，但笔者一直没有把它加上去。

不过好消息是，经过反复查阅和调试，这两天笔者总算把兼容性问题解决了，所以现在大家看到的Cool Papers已经能够渲染数学公式了。这篇文章总结一下解决方案，供大家参考。

摘要带有公式的论文

点击阅读全文...

上一篇文章中我们介绍了“伪逆”，它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$（或$\boldsymbol{B}$）时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解，即
$$\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}$$
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了，这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似（秩不超过$r$的最优近似）”。而要解决这个问题，就需要请出大名鼎鼎的“SVD（奇异值分解）”了。虽然本系列把伪逆作为开篇，但它的“名声”远不如SVD，听过甚至用过SVD但没听说过伪逆的应该大有人在，包括笔者也是先了解SVD后才看到伪逆。

接下来，我们将围绕着矩阵的最优低秩近似来展开介绍SVD。

结论初探

对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$，都可以找到如下形式的奇异值分解（SVD，Singular Value Decomposition）：
$$\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}$$

点击阅读全文...

众所周知，目前主流的LLM，都是基于Causal Attention的Decoder-only模型（对此我们在《为什么现在的LLM都是Decoder-only的架构？》也有过相关讨论），而对于Causal Attention，已经有不少工作表明它不需要额外的位置编码（简称NoPE）就可以取得非平凡的结果。然而，事实是主流的Decoder-only LLM都还是加上了额外的位置编码，比如RoPE、ALIBI等。

那么问题就来了：明明说了不加位置编码也可以，为什么主流的LLM反而都加上了呢？不是说“多一事不如少一事”吗？这篇文章我们从三个角度给出笔者的看法：

1、位置编码对于Attention的作用是什么？

2、NoPE的Causal Attention是怎么实现位置编码的？

3、NoPE实现的位置编码有什么不足？

点击阅读全文...

在《低秩近似之路（二）：SVD》中，我们证明了SVD可以给出任意矩阵的最优低秩近似。那里的最优近似是无约束的，也就是说SVD给出的结果只管误差上的最小，不在乎矩阵的具体结构，而在很多应用场景中，出于可解释性或者非线性处理等需求，我们往往希望得到具有某些特殊结构的近似分解。

因此，从这篇文章开始，我们将探究一些具有特定结构的低秩近似，而本文将聚焦于其中的CR近似（Column-Row Approximation），它提供了加速矩阵乘法运算的一种简单方案。

问题背景

矩阵的最优$r$秩近似的一般提法是
$$\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\label{eq:loss-m2}\end{equation}$$

点击阅读全文...

这篇文章的主角是ID（Interpolative Decomposition），中文可以称之为“插值分解”，它同样可以理解为是一种具有特定结构的低秩分解，其中的一侧是该矩阵的若干列（当然如果你偏好于行，那么选择行也没什么问题），换句话说，ID试图从一个矩阵中找出若干关键列作为“骨架”（通常也称作“草图”）来逼近原始矩阵。

可能很多读者都未曾听说过ID，即便维基百科也只有几句语焉不详的介绍（链接），但事实上，ID跟SVD一样早已内置在SciPy之中（参考scipy.linalg.interpolative），这侧面印证了ID的实用价值。

基本定义

前三篇文章我们分别介绍了伪逆、SVD、CR近似，它们都可以视为寻找特定结构的低秩近似：
$$\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\end{equation}$$

点击阅读全文...