科学空间:2010年10月重要天象
By 苏剑林 | 2010-09-26 | 28676位读者 | Kimi 引用圆满的句号——汽车站的邂逅
By 苏剑林 | 2010-09-23 | 38292位读者 | Kimi 引用21日,是我从北京回家的日子。上午一切都很顺利,很早就赶到机场了,而且飞机也没有晚点。然而,事情却出现了一点意外——
原来由于台风影响,广东正在下暴雨,于是,飞机在广州上空盘旋了半个多小时,本来16:00就可以下的飞机,却到了近17:00才下。庆幸的是,这一次我没有把行李托运,于是下机后马上飞奔门口,乘坐机场快巴。还好,赶上了17:10的快巴。又是两个小时的路程,19:00左右,我到了肇庆汽车总站...
汽车站的售票人员说现在回新兴最早的班车是20:10的,距离现在还有一个小时,我犹豫了一下:这让我等太久了吧...抱着侥幸的心态,我打车到了肇庆的桥西汽车站,希望那儿会有早一点的班车。然而,结果是失望的:途径新兴的车都没有了。这时,在我前边的一个女孩出声了——
级数求和——近似的无穷级数
By 苏剑林 | 2010-09-10 | 61080位读者 | Kimi 引用级数是数学的一门很具有实用性的分支,而级数求和则是级数研究中的核心内容之一。很多问题都可以表示成一个级数的和或积,也就是$\sum_{i=1}^n f(i)$或者是$\prod_{i=1}^n f(i)$类型的运算。其中,$\ln(\prod_{i=1}^n f(i))=\sum_{i=1}^n \ln(f(i))=k$,因此$\prod_{i=1}^n f(i)=e^k$,也就是说,级数求积也可以变为级数求和来计算,换言之我们可以把精力放到级数求和上去。
为了解决一般的级数求和问题,我们考虑以下方程的解:
$$f(x+\epsilon)-f(x)=g(x)\tag{1}$$其中g(x)是已知的以x为变量的函数式,$\epsilon $是常数,初始条件是$f(k)=b$,要求f(x)的表达式。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 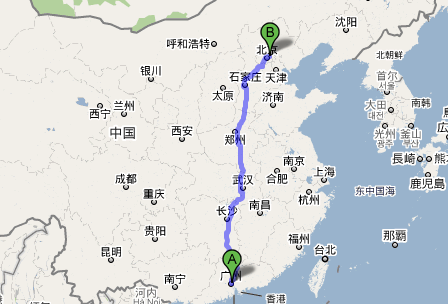

最近评论